A nichrome heating element across 230 V supply cosumes 1.5 kW power and heats upto a temperature of 750∘C. A tungsten bulb across the same supply operates at a much higher temperature of 1600∘C in order to be able to emit light. Does it mean that tungsten bulb necessarily cosumes greater power ?
No, the steady temperature acquired by a resistor (i.e., heating element) depends not only on the power consumed but also on the power loss due to radiation, which inturn depends on the characteristics of a resistor such as surface area, emissivity, etc.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Conceptual Problems
Explore 3 Videos
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Very short Q/A
Explore 7 Videos
- COMMUNICATION SYSTEMSBook:PRADEEPChapter:COMMUNICATION SYSTEMSExercise:MODEL TEST PAPER-2
Explore 9 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:PRADEEPChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Exercise
Explore 191 Videos
Similar Questions
A nichrome heating element connected to a 200 V supply draws an intial current of 2.2 A which settles down after a few seconds to a steady value of 2.0 A. Find the steady temperature of the heating element. The room temperature is 30∘C and the average temperature coefficient of resistance of nichrome is 1.7×10−4per∘C.
View SolutionA heating element using nichrome connected to a 115 V supply draws a current of 1.6A which settles after a few seconds to a steady value of 1.4 A. What is the steady temperature of the heating element if the room temperature is 30∘C ? Temperature coefficient of resistance of nichrome averaged over the temperature range involved is 1.7×10−4.∘C−1.
View Solution
Knowledge Check
A heating element using nichrome connected to a 230 V supply draws an initial current of 3.2 A which settles after a few seconds to a steady value of 2.8 A. What is the steady temperature of the heating element if the room temperature is 27∘C ? Temperature coefficient of resistance of nichrome averaged over the temperature range involved is 1.70×10−4C−1.
A680∘CB51∘CC920∘CD750∘CFigure shows an electrical calorimeter to determine specific heat capacity of an unknown liquid, First of all, the mass of empty calorimeter (a copper container) is measured and suppose it is m1. Then the unknown liquid is poured in it. Now the combined mass of calorimeter+liquid system is measured and let it be m2. So the mass of liquid is (m2−m1). Initially both were at room temperature (θ0).
Now a heater is immeresed in if for time interval t. The voltage drop across the heater is V and current passing through it is I. Due to heat supplied, the temperature of both the liquid and calorimeter will rise simultaneously. After tsec, heater was switched off, and final temperature is θr. If there is no heat loss to surroundings. Heat supplied by the heater=Heat absorbed by the liquid+heat absorbed by the calorimeter (VI)t=(m2−m1)S1(θf−θ0)+m1Sc(θf−θ0)
The specific heat of the liquid S1=(VI)tθf−θ0−m1Sc(m2−m1)
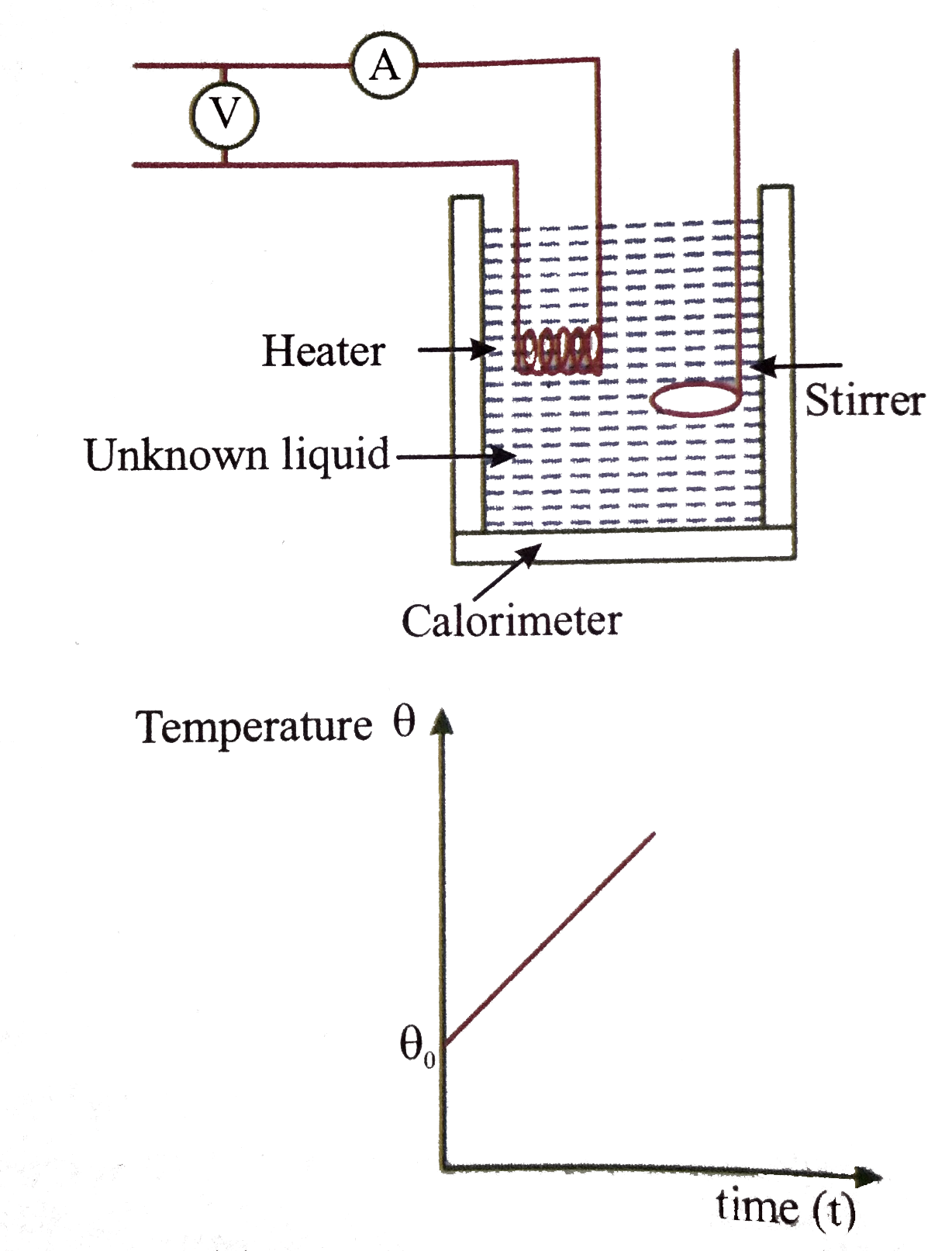
Radiation correction: There can be heat loss to environment. To compensate this loss, a correction is introduced.
Let the heater was on for tsec, and then it is switched off. Now the temperature of the mixture falls due to heat loss to environment. The temperature of the mixture is measured t/2sec. after switching off. Let the fall in temperature during this time is ɛ
Now the corrected final temperature is taken as θf=θf+ɛ
In this experiment voltage across the heater is 100.0V and current is 10.0A, and heater was switched on for t=700.0sec. Initially all elements were at room temperature θ∘=10.0∘C and final temperature was measured as θf=73.0∘C.
Mass of empty calorimeter ws 1.0kg and the combined mass of calorimeter + liquid is 3.0kg. The specific heat capacity of the calorimeter =3.0×103J/kg∘C. The falls in temperature 350 second after switching off the heater was 7.0∘C. Find the specific heat capacity of the unknown liquid in proper significant figures.A3.5×103J/kg∘CB3.50×103J/kg∘CC4.0×103J/kg∘CD3.500×103J/kg∘CFigure shows an electrical calorimeter to determine specific heat capacity of an unknown liquid, First of all, the mass of empty calorimeter (a copper container) is measured and suppose it is m1. Then the unknown liquid is poured in it. Now the combined mass of calorimeter+liquid system is measured and let it be m2. So the mass of liquid is (m2−m1). Initially both were at room temperature (θ0).
Now a heater is immeresed in if for time interval t. The voltage drop across the heater is V and current passing through it is I. Due to heat supplied, the temperature of both the liquid and calorimeter will rise simultaneously. After tsec, heater was switched off, and final temperature is θr. If there is no heat loss to surroundings. Heat supplied by the heater=Heat absorbed by the liquid+heat absorbed by the calorimeter (VI)t=(m2−m1)S1(θf−θ0)+m1Sc(θf−θ0)
The specific heat of the liquid S1=(VI)tθf−θ0−m1Sc(m2−m1)
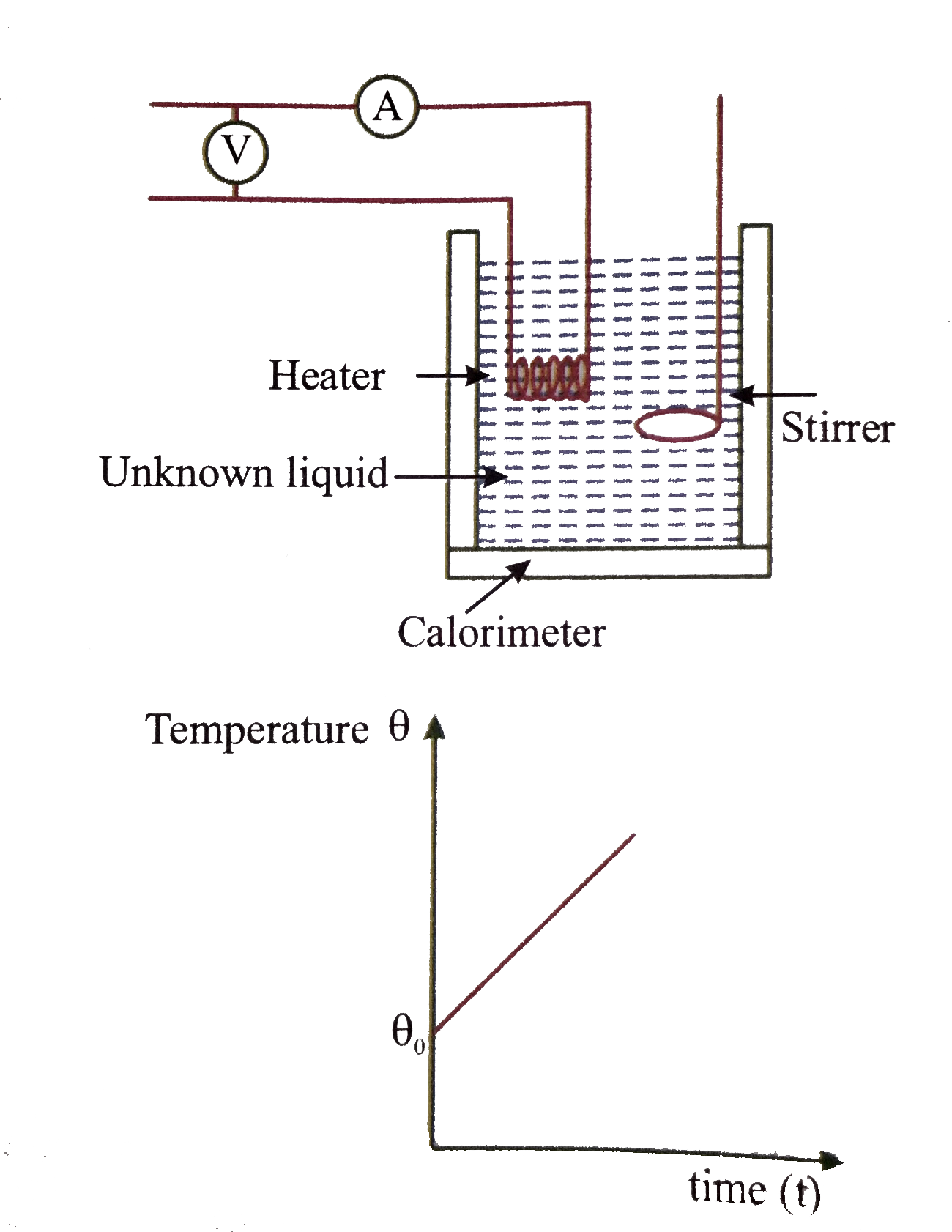
Radiation correction: There can be heat loss to environment. To compensate this loss, a correction is introduced.
Let the heater was on for tsec, and then it is switched off. Now the temperature of the mixture falls due to heat loss to environment. The temperature of the mixture is measured t/2sec. after switching off. Let the fall in temperature during this time is ɛ
Now the corrected final temperature is taken as θf=θf+ɛ
If mass and specific heat capacity of calorimeter is negligible, what would be maximum permissible error in Sl. Use the date mentioned below.
m1→, Sl→0, m2=1.00kg,
V=10.0V, I=10.0A,
t=1.00×102sec, θ0=15∘C,
Corrected θ1=65∘CA4%B5%C8%D12%
A heating element using nichrome connected to a 230 V supply draws an initial current of 3.2 A which settles after a few seconds to a steady value of 2.8 A. What is the steady temperature of the heating element if the room temperature is 27.0∘C ? Temperature coefficient of resistance of nichrome averaged over the temperature range involved is 1.70×10−4∘C−1 .
View SolutionA heating element using nichrome connected to a 230 V supply draws an initial current of 3.2 A which settles after a few seconds to a steady value of 2.8 A. What is the steady temperature of the heating element if the room temperature is 27∘C ? Temperature coefficient of resistance of nichrome averaged over the temperature range involved is 1.70×10−4C−1.
View SolutionAn electric toaster uses nichrome for its heating element. When a negligibly small current passes through it. It resistance at room temperature (27.0∘C) is found to be 75.3Ω. When the toaster is connected to a 230V supply, the current settles, after a few seconds, to a steady value of 2.68A. What is steady temperature of the nichrome element? The temperature coefficient of resistance of nichrome averaged over the temperature range involved , 1.70×10−4C−1
View SolutionFigure shows an electrical calorimeter to determine specific heat capacity of an unknown liquid, First of all, the mass of empty calorimeter (a copper container) is measured and suppose it is m1. Then the unknown liquid is poured in it. Now the combined mass of calorimeter+liquid system is measured and let it be m2. So the mass of liquid is (m2−m1). Initially both were at room temperature (θ0).
Now a heater is immeresed in if for time interval t. The voltage drop across the heater is V and current passing through it is I. Due to heat supplied, the temperature of both the liquid and calorimeter will rise simultaneously. After tsec, heater was switched off, and final temperature is θr. If there is no heat loss to surroundings. Heat supplied by the heater=Heat absorbed by the liquid+heat absorbed by the calorimeter (VI)t=(m2−m1)S1(θf−θ0)+m1Sc(θf−θ0)
The specific heat of the liquid S1=(VI)tθf−θ0−m1Sc(m2−m1)
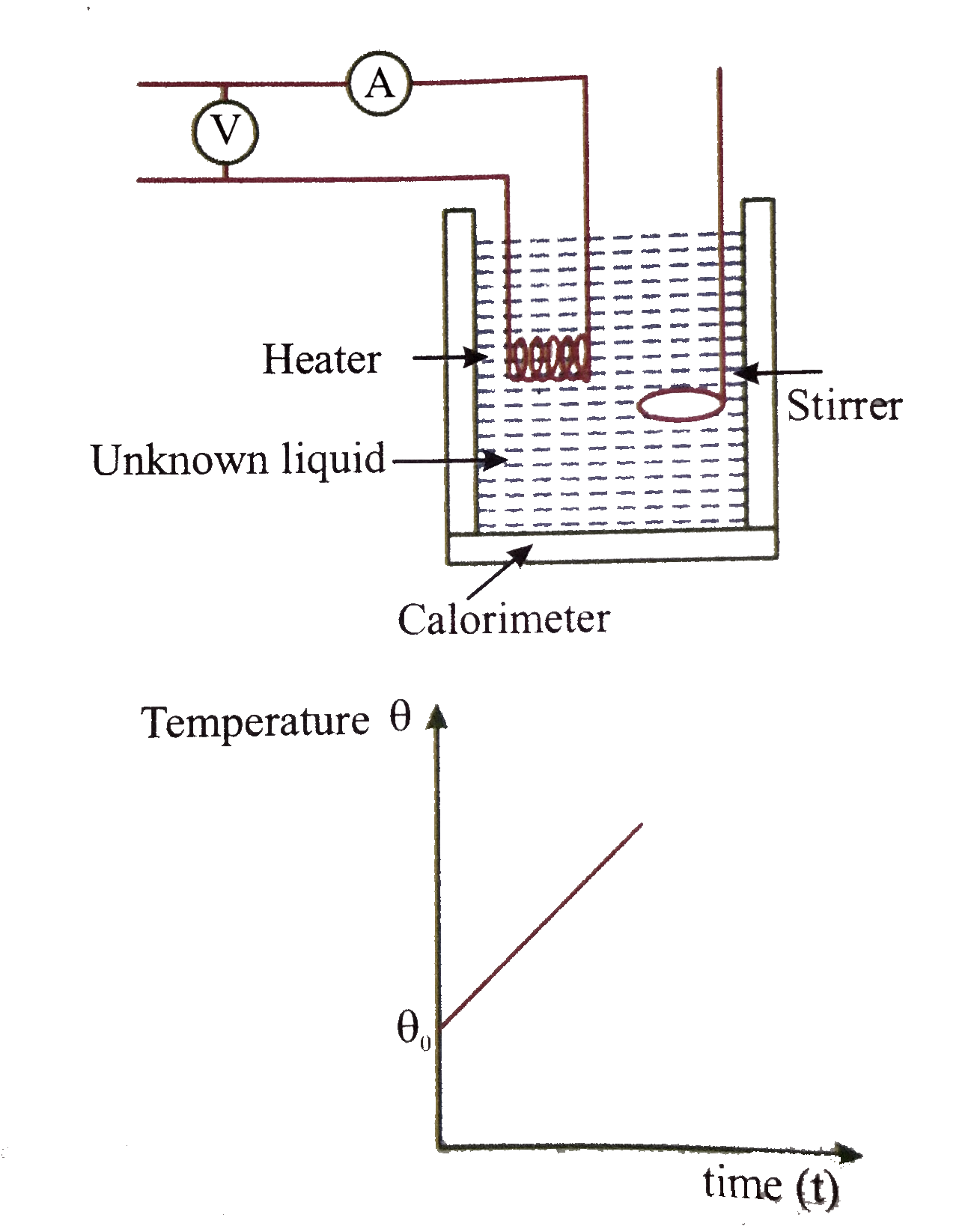
Radiation correction: There can be heat loss to environment. To compensate this loss, a correction is introduced.
Let the heater was on for tsec, and then it is switched off. Now the temperature of the mixture falls due to heat loss to environment. The temperature of the mixture is measured t/2sec. after switching off. Let the fall in temperature during this time is ɛ
Now the corrected final temperature is taken as θf=θf+ɛ
If the system were losing heat according to Newton's cooling law, the temperature of the mixture would change with time according to (while heater was on)
View SolutionA fuel cell is a cell that is continuously supplied with an oxidant and a reductant so that it can deliver a current indefinitely. Fuel cell offer the possibility of achieving high thermodynamic efficiency in the conversion of Gibbs energy into mechanical work. Internal combustion engines at best convert only the fraction (T2−T1)T2 of heat of combustion into mechanical work. While the thermodynamic efficiency of the fuel cell is give by, η=|ΔG||ΔH|, where ΔG is the Gibbs energy change for the cell reaction and ΔH is the enthalpy change of the cell reaction. This efficiency can be upto 80%-90% also in contrast to normal heat engine efficiency which are generally about 40%

Fuel cells may be classified according to the temperature range in wich they operate low temperature (25 to 100∘C), medium temperature (100 to 500∘C)), high temperature (500to1000∘C) and very high temperature is that catalyst for the various steps in the process are not so necessary. Polarization of a fuel cell reduces the current. Polarization is the result of slow reactions or processes such as diffusion in the cell. The figure indicates the construction of hydrogen-oxygen fuel cell with a solid electrolyte, which is an ion exchange membrane. The membrane is impermeable to the reactant gases, but is permeable to hydrogen ions, which carry the current between the electrodes. To facillitate the operation finely divided platinum that function as a catalyst. Water is drained out of the cell during operation. Fuel cells of this general type have been used successfully in the space program and are quite efficient. their disadvantages for large-scale commercial application are that hydrogen presetns storage problems, and platinum is an expensive catalyst. Cheaper catalysts have been found for higher temperature operatureof hydrogen-oxygen fuel cells. Fuel cells taht use hydrocarbons and air have been developed, but their power per unit weight is too low to make them practical in ordinary automobiles. Better catalysts are needed. A hydrogen-oxygen fuel cell may hae an acidic or alkaline electrolyte. The half-cell reactions are:
12O2(g)+2H++2e−→H2O(l)E∘=1.2288V
2H++2e−→H2(g)E∘=0
H2(g)+12O2(g)→H2O(l)E∘=1.2288V
or 12O2(g)+H2O(g)+2e−→2OH−E∘=0.4009V
2H2O(l)+2e−→H2(g)+2OH−E∘=−0.8279V
H2(g)+12O2(g)→H2O(l)E∘=1.2288V
To maximize the power per unit mass of an electrochemical cell, the electronic and electrolytic resistances of the cell must be minimized. than aqueous solutions, high-temperature electrochemical cells are of special interest for practical applications. High temperature also allow the use of liquid metal electrode, which makes possibel high current densities than solid electrodes.
If 567.5 mL of H2 gas at STP is fed into and is consumed by the cell in 10minutes, then what is the current output (in A) of the fuel cell?
View Solution

