The emf of the cell is 1.8 V and internal resistance is 2/3Ω, calculate the current in the 3Oemga resistance and the power dissipated in the whole circuit.

The equivalent circuit is shown in figure.
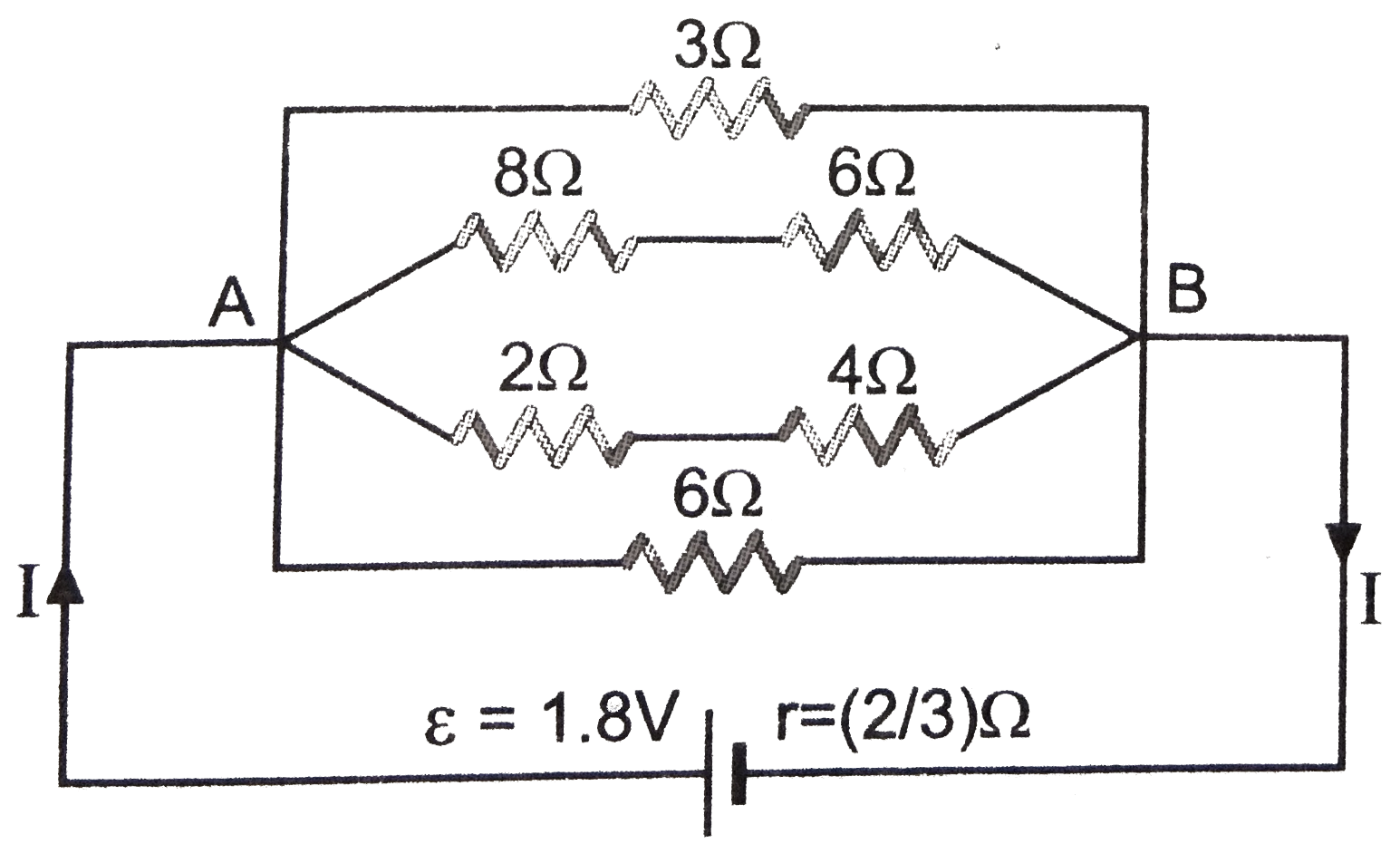
Effective resistance Rp between A and B will be
1Rp=13+114+16+16=3142
or Rp=4231Ω
Current from the cell,
I=εRp+r=1.84231+23=0.89A
Potential diff. between A and B,
VA−VB=IRp=0.89×4231=1.21V
Current in 3Ω resistance =1.213=0.4A
Power dissipated in the whole circuit (including the cell)is
P=I2(R+r)=(0.89)2(4231+23)
=1.6 watt
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Conceptual Problems
3 Videos
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Very short Q/A
7 Videos
- COMMUNICATION SYSTEMSBOOK - PRADEEPCHAPTER - COMMUNICATION SYSTEMSEXERCISE - MODEL TEST PAPER-2
9 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise
191 Videos
Similar Questions
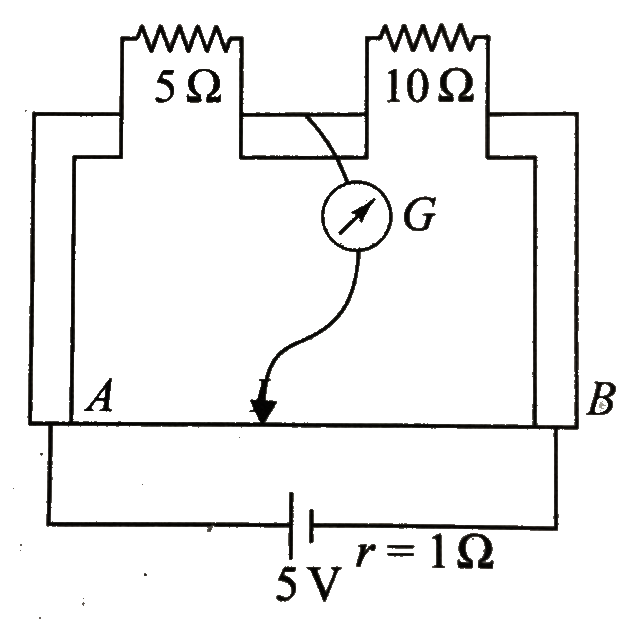
In a meter bridge circuit, the two resistances in the gap are 5Ω and 10Ω. The wire resistance is 4Ω. The emf of the cell connected at the ends of the wire is 5V and its internal resistance is 1Ω. What current will flow through the galvenometer of resistance 30Ω if the contact is made at the midpoint of wire ?
View SolutionA resistor is connected to a battery of emf 10 V and internal resistance 0.3Ω. What is the resistance of the resistor to be inserted in the circuit for the circuit current 1.2A?
View Solution
Knowledge Check
A battery of 20 cells is charged by 220 V with a charging current of 15 A . If the emf of each cell is 2 V and internal resistance is 0.1Ω , then the series resistance required to be placed in the circuit will be
A16ΩB10ΩC12ΩD14ΩA battery of 20 cells (each having e.m.f. 1.8V and internal resistance 0.1Ω is charged by 220 volts and the charging current is 15A. Calculate the resistance to be put in the circuit.
A4m/sB10ms2C5ms2D2√2ms2Three cells are connected to an external resistance as shown in the figure. Each of the cells has emf 10 V and internal resistance 2Ω.
If the external resistance is 6Ω. Find the current in the circuit.A2AB2.5 AC3AD3.5 A
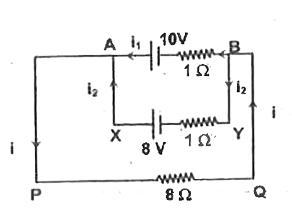
Two cells having emf's of 10 V and 8 V, and internal resistance of 1Ω(each) are connected as shown with an external resistance of 8Ω Find the current flowing through the circuit.
View SolutionCalculate the current drawn from the battery of emf 15V and internal resistance 0.5Ω in the circuit shown in Fig. 6.12. Also find the power dissipated in thd 6Ω resistor.
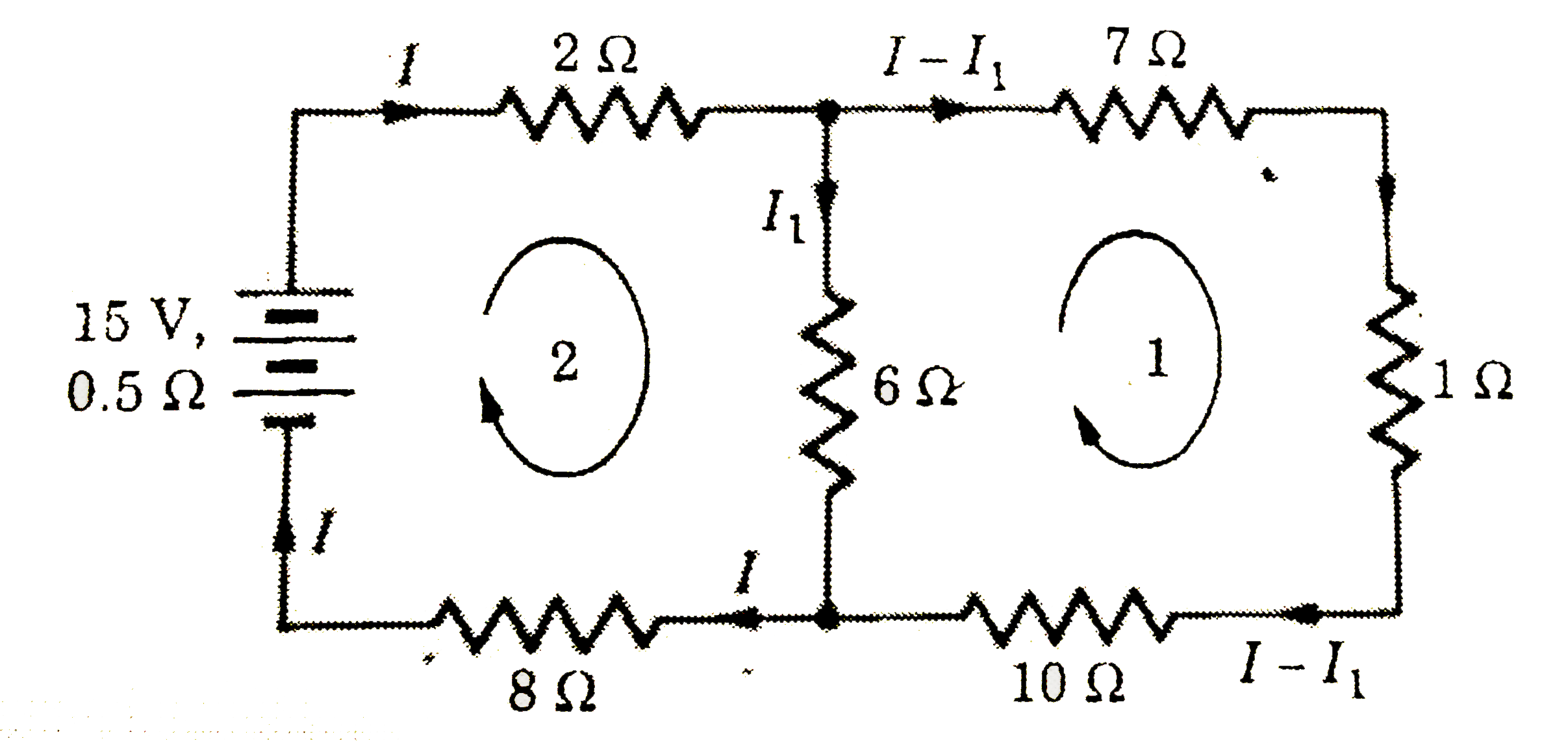
View SolutionIn the circuit, the cells E1andE2 have emfs of 4V and 8V and internal resistance 0.5Ωand1.0Ω, respectively. Calculate the current through 6Ω resistance.
View SolutionMaximum current produced by a cell of emf 10 V and internal resistance 2Ω is
View SolutionMaximum current produced by a cell of emf 10 V and internal resistance 2Ω is
View Solution