Twelve wire, each having resistance r, are joined to form a cube as shown in figure.Find the equivalent resistance between the end of a face diagonal such as aandc.

Let ABCDKLMN be the skeleton cube formed by joining twelve equal wires each of resistance r.
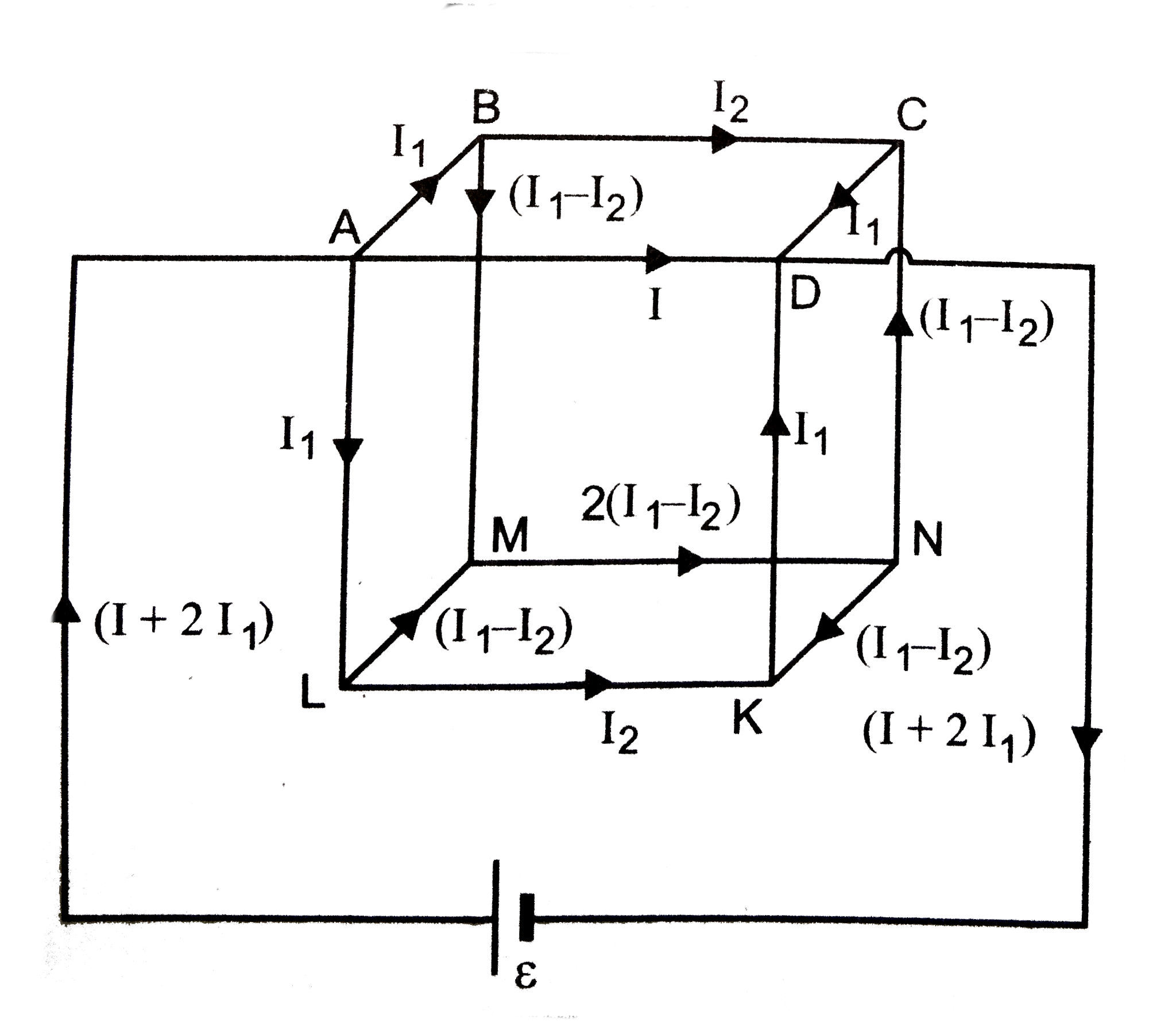
Let the current enter the cube at corner A and after passing through all twelve wires, let the current leave at D, other corner of the same edge of the cube.
For the sake of convenience, let us suppose that the total current is (I+2I1). At A, this current is divided into three parts : I along AD and I1 each along AB and AL as the resistance along AB and AL are the same but along AD, it is different. At the points B and L, current is further divided into two unequal parts. The distribution of current in the various arms of skeleton cube is shown according to Kirchhoff's First rule. The current leaving the cube at D is again (I+2I1). Applying Kirchhoff's Second rule to the closed meah ABCDA , we get
I1r+I2r+I1r−Ir=0
or 2I1+I2=I
For closed mesh BCNMB ,
I2r−(I1−I2)r−2(I1−I2)r−(I1−I2)r=0
or I2r=4(I1−I2)r
or I2=4I1−4I2
or 5I2=4I1orI2=45I1
From(i) , I=2I1+45I1=145I1
For closed mesh ADεA, Ir=ε
Where ε is the emf of the cell of negligible internal resistance.
If R is the total resistance between the two corners of the same edge of the cube, then applying Kirchhoff's second rule for the closed mesh ADε A, we get,
(I+2I1)R=εor(145I1+2I1)R=ε
or 245I1R=ε
From (iii) and (iv), 145I1r=ε
From (v) and (vi),
245I1R=145I1rorR=1424r=712r
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Conceptual Problems
Explore 3 Videos
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Very short Q/A
Explore 7 Videos
- COMMUNICATION SYSTEMSBook:PRADEEPChapter:COMMUNICATION SYSTEMSExercise:MODEL TEST PAPER-2
Explore 9 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:PRADEEPChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Exercise
Explore 191 Videos
Similar Questions
Twelve wire, each having equal resistance r, are joined to form a cube as shown in figure.Find the equivalent resistance between the diagonally opposite points a and f.

View SolutionFive resistances are joined as shown in the figure.
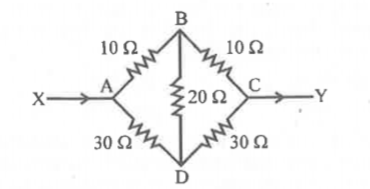
The equivalent resistance between the points X and Y is
View Solution
Knowledge Check
In the network shown in the figure, the equivalent resistance between A and C is
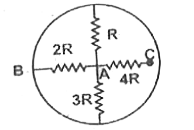 A10 RB(6/11)RC(12/15)RD(50/11)R
A10 RB(6/11)RC(12/15)RD(50/11)RFour identical resistances each having value R are arranged as shown in Figure. Find the equivalent resistance between A and B.
 ARB2RC3RD4R
ARB2RC3RD4R
Twelve capacitors, each having capacitors, C, are joined to from a cube as shown. Find the equivalent capacitance between the ends of
(a) Digitonal i.e., between A and B.
(b) Face diagonal i.e., between A and C.
(c) side of cube i.e., between A and D.

View SolutionFive resistance are connected as shown in the figure. The equivalent resistance between points A and C is
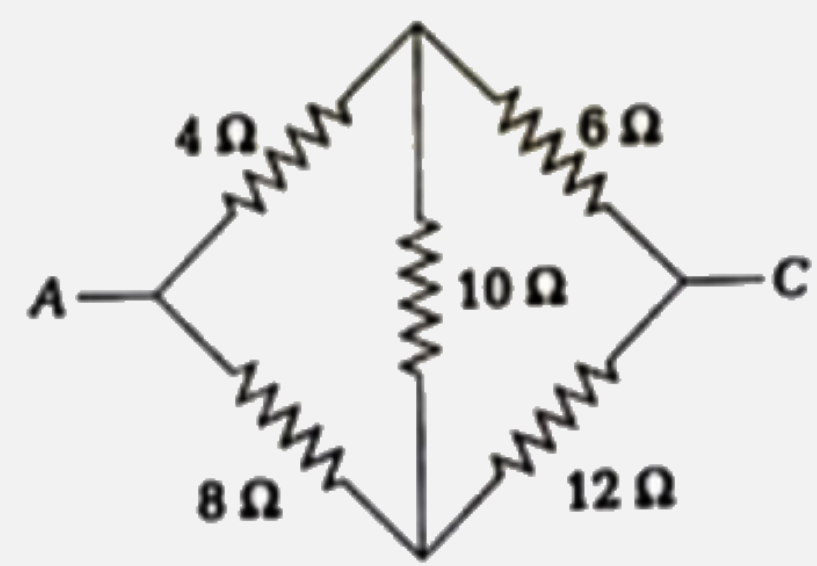
View SolutionIdnetical resistor each of resistance r are connected as shown in figure. Calculate equivalent resistance between A and E.
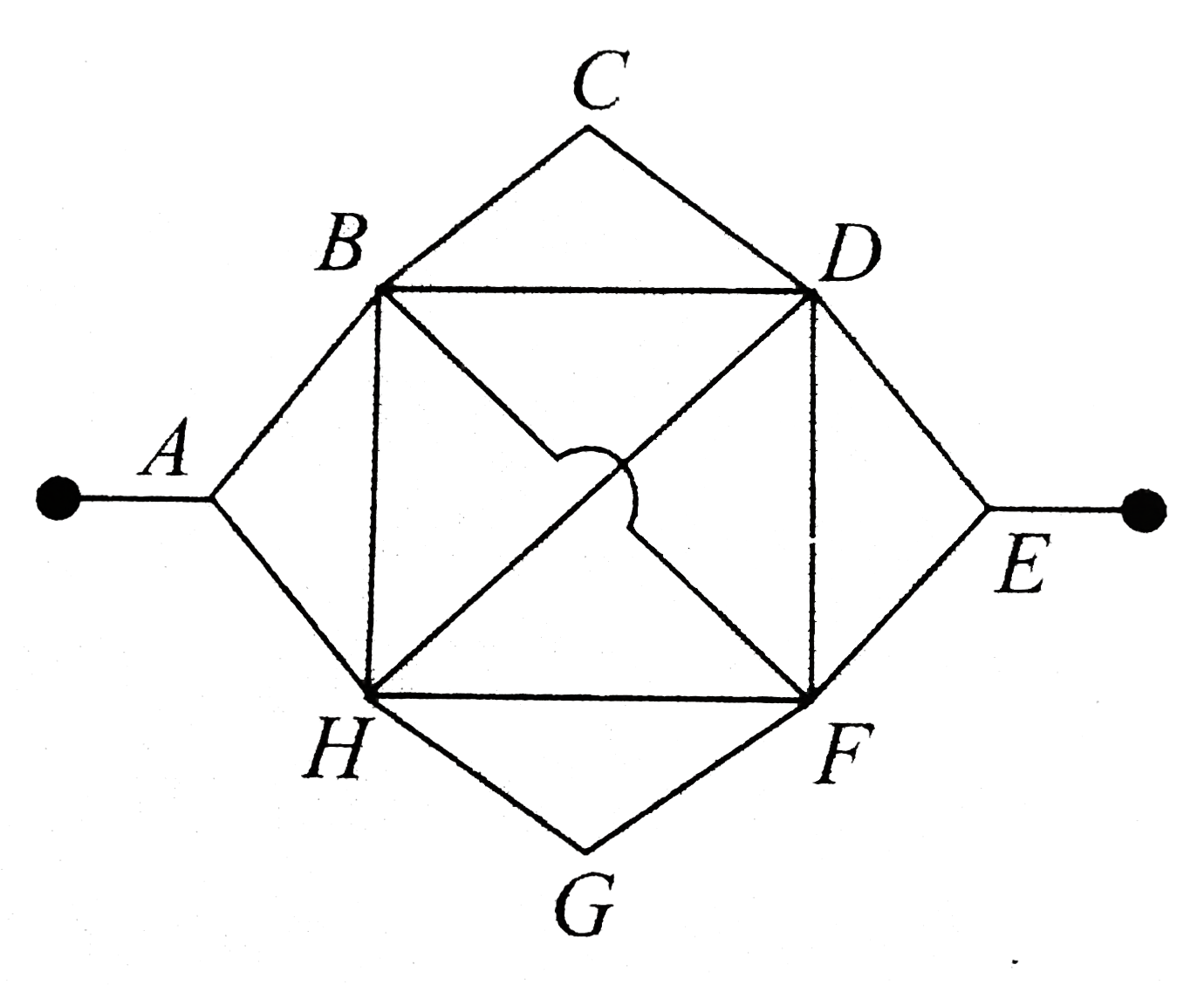
View SolutionEach resistance is of 1Ω in the circuit diagram shown in figure. Find out equivalent resistance between A and B.
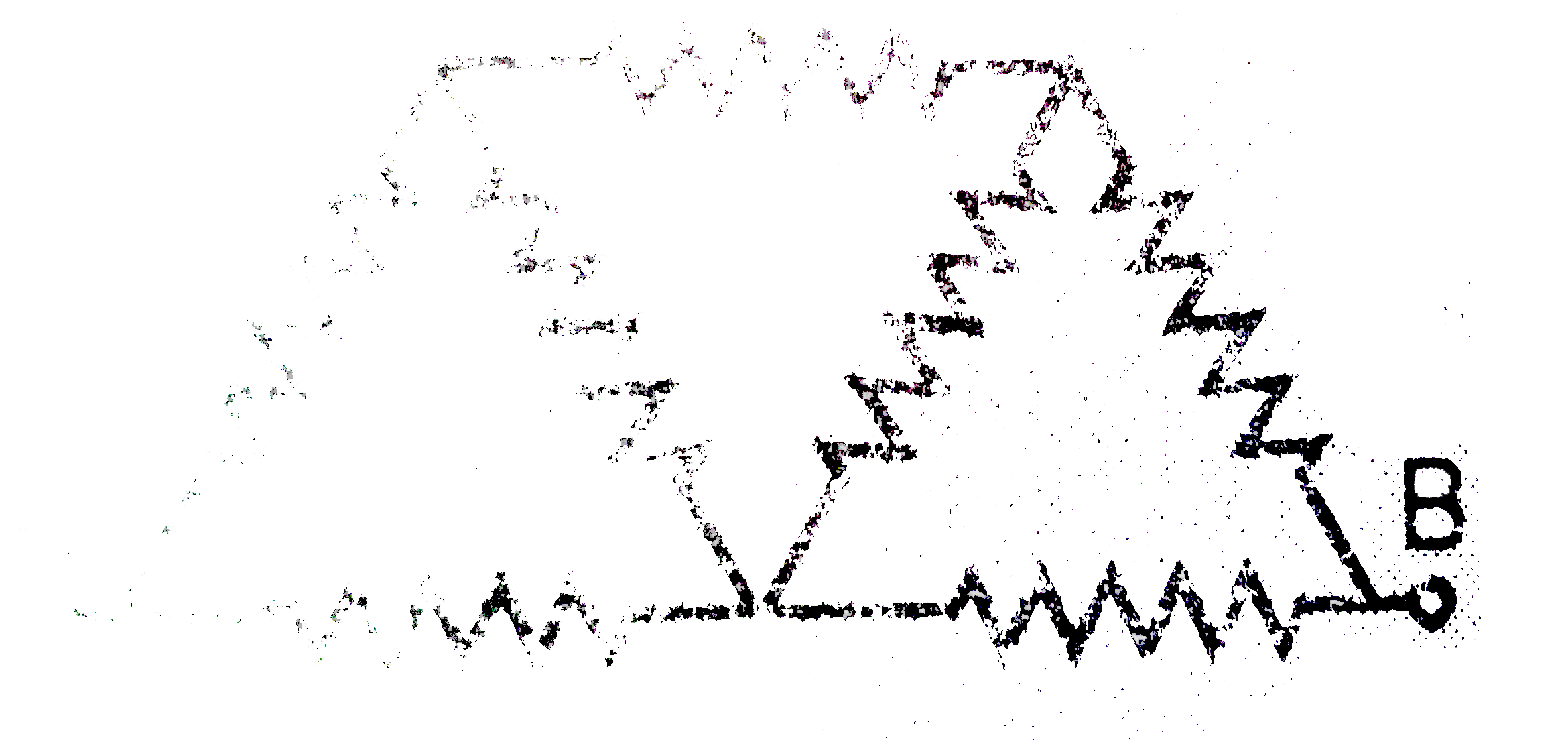
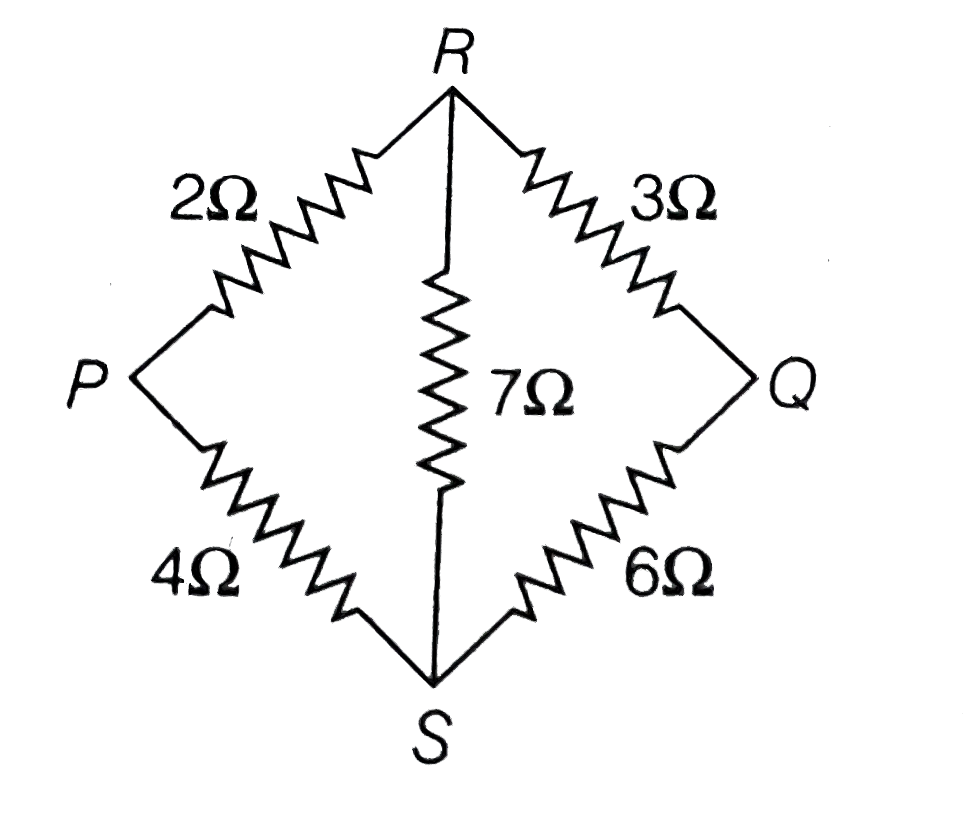
View SolutionFive resistance are connected as shown in the figure . The equivalent resistance between P and Q will be
View Solution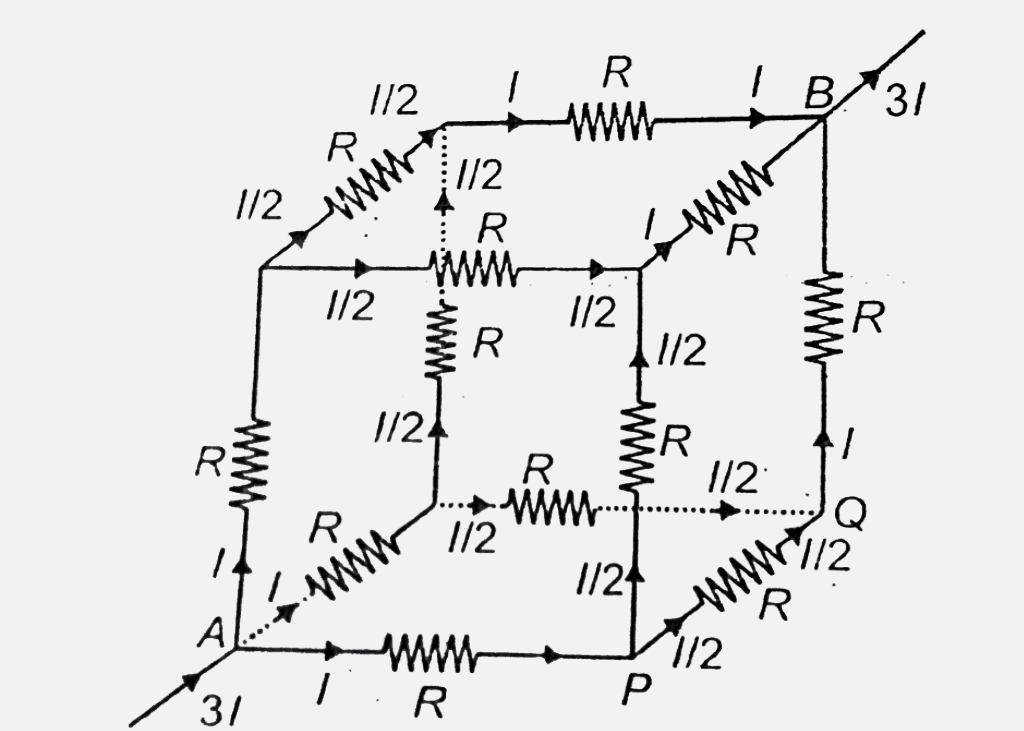
Tweve identical resistance each of resistance R are joined to form a cube as shown in figure.
Find resistance of the combination across AB
View Solution