Three materials A, B and C have electrical conductivities σ,2σ and 2σ respectively. Their numbers densities of free electrons are 2 n, n and 2n respectively. For which material is a average collision time of free electrons maximum?
To determine which material has the maximum average collision time (relaxation time) of free electrons, we can use the relationship between electrical conductivity (σ), number density of free electrons (n), and average collision time (τ).
1. Understand the relationship: The electrical conductivity (σ) of a material is given by the formula:
σ=ne2τm
where:
- n is the number density of free electrons,
- e is the charge of an electron,
- τ is the average collision time,
- m is the mass of an electron.
2. Rearranging the formula: We can rearrange this formula to express the average collision time (τ):
τ=σmne2
This shows that τ is directly proportional to the conductivity (σ) and inversely proportional to the number density of free electrons (n).
3. Identify the given values:
- For material A:
- Conductivity, σA=σ
- Number density, nA=2n
- For material B:
- Conductivity, σB=2σ
- Number density, nB=n
- For material C:
- Conductivity, σC=2σ
- Number density, nC=2n
4. Calculate τ for each material:
- For material A:
τA=σm2ne2=σm2ne2
- For material B:
τB=2σmne2=2σmne2
- For material C:
τC=2σm2ne2=σmne2
5. Compare τ values:
- We have:
- τA=σm2ne2
- τB=2σmne2
- τC=σmne2
- To compare these values, we can express them in a common format:
- τA:τB:τC=σ2n:2σn:σn
- Simplifying gives:
- τA:τB:τC=1:4:2
6. Conclusion: From the ratios, we see that τB is the largest. Therefore, the average collision time of free electrons is maximum for material B.
Final Answer:
Material B has the maximum average collision time of free electrons.
σ=ne2τm
where:
- n is the number density of free electrons,
- e is the charge of an electron,
- τ is the average collision time,
- m is the mass of an electron.
τ=σmne2
This shows that τ is directly proportional to the conductivity (σ) and inversely proportional to the number density of free electrons (n).
- For material A:
- Conductivity, σA=σ
- Number density, nA=2n
- For material B:
- Conductivity, σB=2σ
- Number density, nB=n
- For material C:
- Conductivity, σC=2σ
- Number density, nC=2n
- For material A:
τA=σm2ne2=σm2ne2
- For material B:
τB=2σmne2=2σmne2
- For material C:
τC=2σm2ne2=σmne2
- We have:
- τA=σm2ne2
- τB=2σmne2
- τC=σmne2
- τA:τB:τC=σ2n:2σn:σn
- Simplifying gives:
- τA:τB:τC=1:4:2
Material B has the maximum average collision time of free electrons.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Long Q/A
Explore 1 Video
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Value based
Explore 2 Videos
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Very short Q/A
Explore 7 Videos
- COMMUNICATION SYSTEMSBook:PRADEEPChapter:COMMUNICATION SYSTEMSExercise:MODEL TEST PAPER-2
Explore 9 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:PRADEEPChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Exercise
Explore 191 Videos
Similar Questions
Using the microscopic form of Ohm's law (J=σE) , prove that conductivity of a metal can be written as σ=neμ. Here n is the number of free electrons per unit volume and μ is mobility of free electrons . In case of semiconductors there are two types of conduction particles, one is free electrons and the other is known as a hole. Charge on the hole may be assumed to be equal and opposite of that on electron. The number density of free electrons and holes in the semiconducting material are n and p respectively. Assuming μeandμh as mobility of free electrons and holes respectively , write the exopression of conductivity of the semiconducting material.
View SolutionThree concentric spherical metallic shells A, B and C of radii a, b and c (a lt b ltc) have surface charge densities σ, −σ and σ respectively.
(i) Find the potential of the three shells A, B and C.
(ii) If the shells A and C are at the same potential, obtain the relation between the radii a, b and c.
View Solution
Knowledge Check
Electrical conductivies of Ge and Na are σ1 and σ2 respectively. If these substances are heard, then
Aσ1 decreases and σ2 increasesBboth σ1 and σ2 decreasesCboth σ1 and σ2 increasesDσ1 increases and σ2 decreasesσ1 and σ2 are the electrical conductivities of Ge and Na respectively. If these substances are heated, then
ABoth σ1 and σ2 increaseBσ1 increases and σ2 decreaseCσ1 decreases and σ2 increasesDBoth σ1 and σ2 decreaseThree non-conducting large parallel plates have surface charge densities σ,−2σand4σ respectively as shown in the figure. The electric field at the point P is
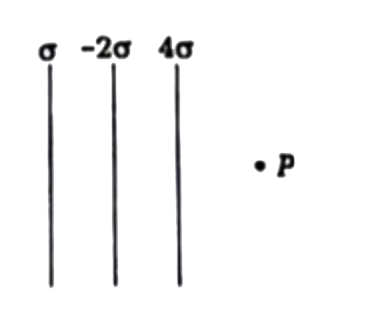 Aσε0Bσ2ε0C3σ2ε0D3σε0
Aσε0Bσ2ε0C3σ2ε0D3σε0
Three concentric spherical metallic shells A, B and C of radii a, b and c (a lt b ltc) have surface charge densities σ, −σ and σ respectively.
(i) Find the potential of the three shells A, B and C.
(ii) If the shells A and C are at the same potential, obtain the relation between the radii a, b and c.
View SolutionThree concentric spherical metallic shells A,B,andC of radii a,b,andc(a<b<c) have surface charge densities σ,−σ and σ, respectively.
If VA,VB and VC are potential of shells A, B and C, respectively, match the columns
Column AColumn Ba.VAi.σε0[a2−b2+c2c]b.VBii.σ2ε0[a2b−b+c]c.VCiii.σε0[a−b+c]
View SolutionIf n represents density of free electrons in a conducting wire, its resistance is proportional to
View SolutionThree concentric charged metallic spherical shells A, B and C have radii a,b and c, charge densities σ,−σ and σ and potentials VA,VB and VC respectively. Then which of the following relations is correct?
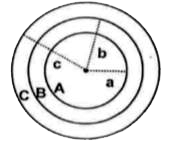
View SolutionThree concentric metallic spherical shells A,B and C of radii a,band c(a<b<c) have surface charge densities −σ,+σand -sigma respectively,thepotentialofshellA is
View Solution

