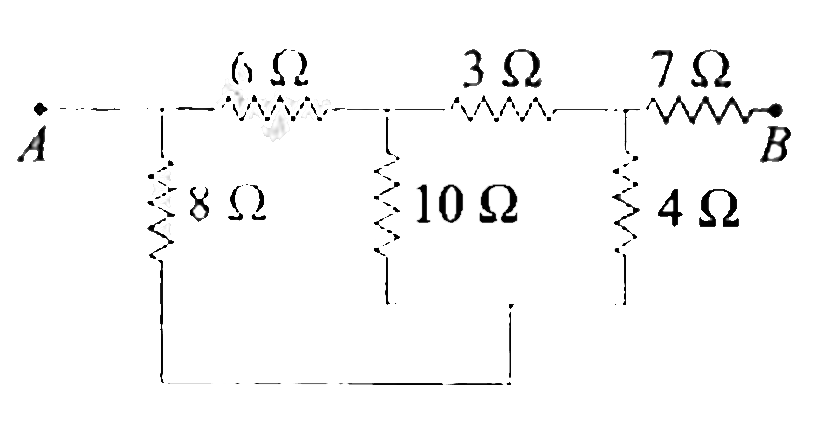
In the given network of resistors, Find the equivalent resistance (i) between the points A and B (ii) between the points A and D (iii) between the points A and C.
To find the equivalent resistance in the given network of resistors between points A and B, A and D, and A and C, we will follow these steps:
Step 1: Find the Equivalent Resistance between Points A and B (R_AB)
1. Identify the resistors between A and B: In the circuit, we have a 3Ω resistor and a 7Ω resistor connected in series.
2. Calculate the total resistance in series:
RAB=R1+R2=3Ω+7Ω=10Ω
3. Identify the next resistors in parallel: There are two 10Ω resistors in parallel.
4. Calculate the equivalent resistance of the two 10Ω resistors in parallel:
Req=R1×R2R1+R2=10Ω×10Ω10Ω+10Ω=100Ω220Ω=5Ω
Thus, the equivalent resistance between points A and B is 5Ω.
Step 2: Find the Equivalent Resistance between Points A and D (R_AD)
1. Identify the resistors between A and D: The path from A to D includes a 10Ω resistor and a 15Ω resistor in series.
2. Calculate the total resistance in series:
RAD1=10Ω+5Ω=15Ω
3. Identify the next resistors in parallel: The 15Ω resistor is in parallel with a 10Ω resistor.
4. Calculate the equivalent resistance of the 10Ω and 15Ω resistors in parallel:
Req1=10Ω×15Ω10Ω+15Ω=150Ω225Ω=6Ω
5. Now, add the 6Ω resistance to the 3Ω resistor in series:
RAD=6Ω+3Ω=9Ω
Thus, the equivalent resistance between points A and D is 39/16Ω or approximately 2.44Ω.
Step 3: Find the Equivalent Resistance between Points A and C (R_AC)
1. Identify the resistors between A and C: The path includes a 10Ω resistor and a 5Ω resistor in series.
2. Calculate the total resistance in series:
RAC1=10Ω+5Ω=15Ω
3. Identify the next resistors in parallel: The 3Ω and 7Ω resistors are in series, giving:
RAC2=3Ω+7Ω=10Ω
4. Now, find the equivalent resistance of the 15Ω and 10Ω resistors in parallel:
Req2=15Ω×10Ω15Ω+10Ω=150Ω225Ω=6Ω
5. Now, add the 6Ω resistance to the 5Ω resistor in series:
RAC=6Ω+5Ω=11Ω
Thus, the equivalent resistance between points A and C is 3.75Ω.
Summary of Results:
- R_AB = 5Ω
- R_AD = 39/16Ω (approximately 2.44Ω)
- R_AC = 3.75Ω
2. Calculate the total resistance in series:
RAB=R1+R2=3Ω+7Ω=10Ω
3. Identify the next resistors in parallel: There are two 10Ω resistors in parallel.
4. Calculate the equivalent resistance of the two 10Ω resistors in parallel:
Req=R1×R2R1+R2=10Ω×10Ω10Ω+10Ω=100Ω220Ω=5Ω
2. Calculate the total resistance in series:
RAD1=10Ω+5Ω=15Ω
3. Identify the next resistors in parallel: The 15Ω resistor is in parallel with a 10Ω resistor.
4. Calculate the equivalent resistance of the 10Ω and 15Ω resistors in parallel:
Req1=10Ω×15Ω10Ω+15Ω=150Ω225Ω=6Ω
5. Now, add the 6Ω resistance to the 3Ω resistor in series:
RAD=6Ω+3Ω=9Ω
2. Calculate the total resistance in series:
RAC1=10Ω+5Ω=15Ω
3. Identify the next resistors in parallel: The 3Ω and 7Ω resistors are in series, giving:
RAC2=3Ω+7Ω=10Ω
4. Now, find the equivalent resistance of the 15Ω and 10Ω resistors in parallel:
Req2=15Ω×10Ω15Ω+10Ω=150Ω225Ω=6Ω
5. Now, add the 6Ω resistance to the 5Ω resistor in series:
RAC=6Ω+5Ω=11Ω
- R_AB = 5Ω
- R_AD = 39/16Ω (approximately 2.44Ω)
- R_AC = 3.75Ω
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Conceptual Problems
3 Videos
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Very short Q/A
7 Videos
- COMMUNICATION SYSTEMSBOOK - PRADEEPCHAPTER - COMMUNICATION SYSTEMSEXERCISE - MODEL TEST PAPER-2
9 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise
191 Videos
Similar Questions
Knowledge Check
Find the equivalent resistance between the points a and b
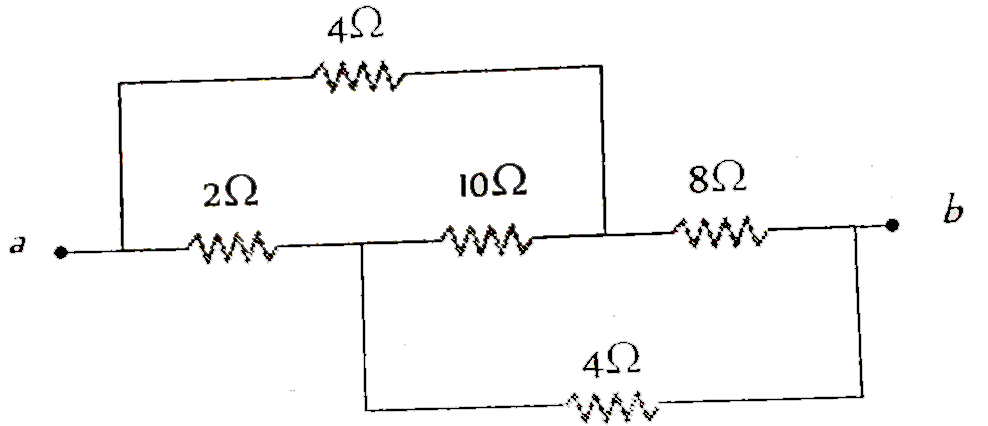 A2ΩB4ΩC8ΩD16Ω
A2ΩB4ΩC8ΩD16ΩFind the equivalent resistance between the points a and b
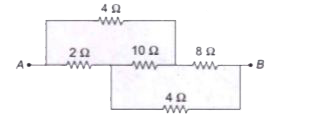 A2ΩB4ΩC8ΩD16Ω
A2ΩB4ΩC8ΩD16ΩFind the equivalent resistance between the point A and B
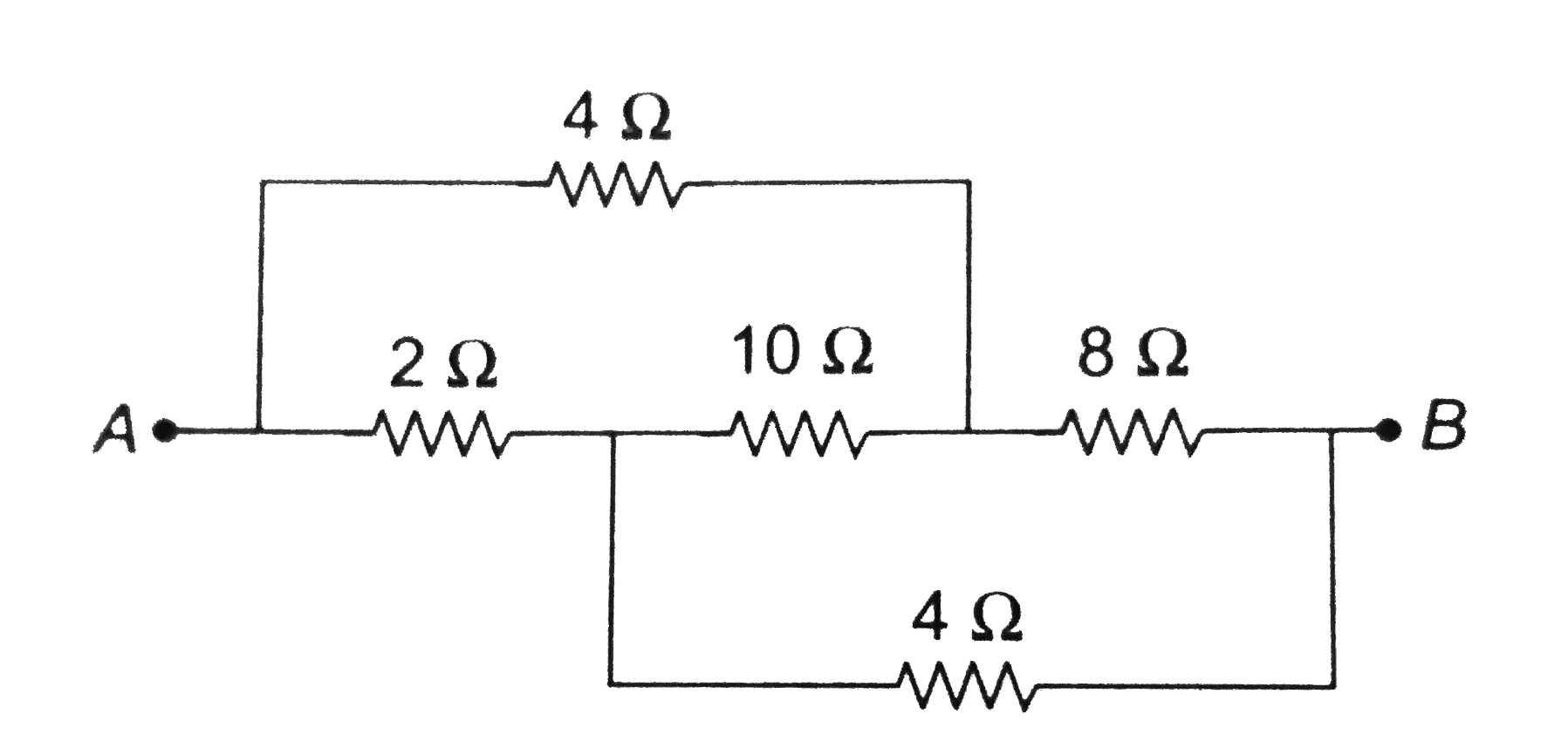 A2ΩB4ΩC8ΩD16Ω
A2ΩB4ΩC8ΩD16Ω
The network of resistors. Find the equivalent resistance between points A and D.
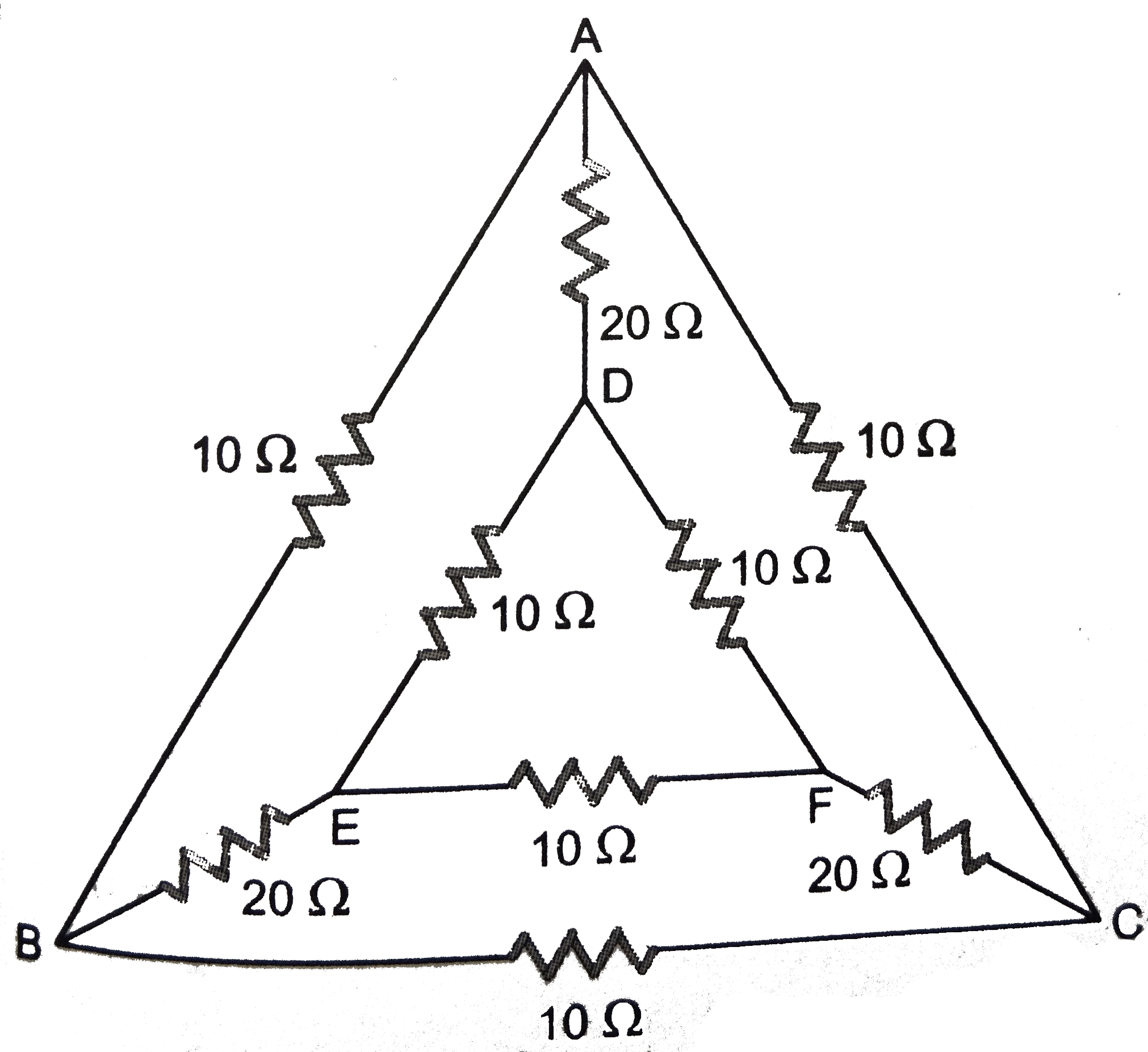
View SolutionFind the equivalent resistance of the circuit between the points A and B

View SolutionFind in the given network of resistors, the equivalent resistance between the points A and B, between A and D, and between A and C.
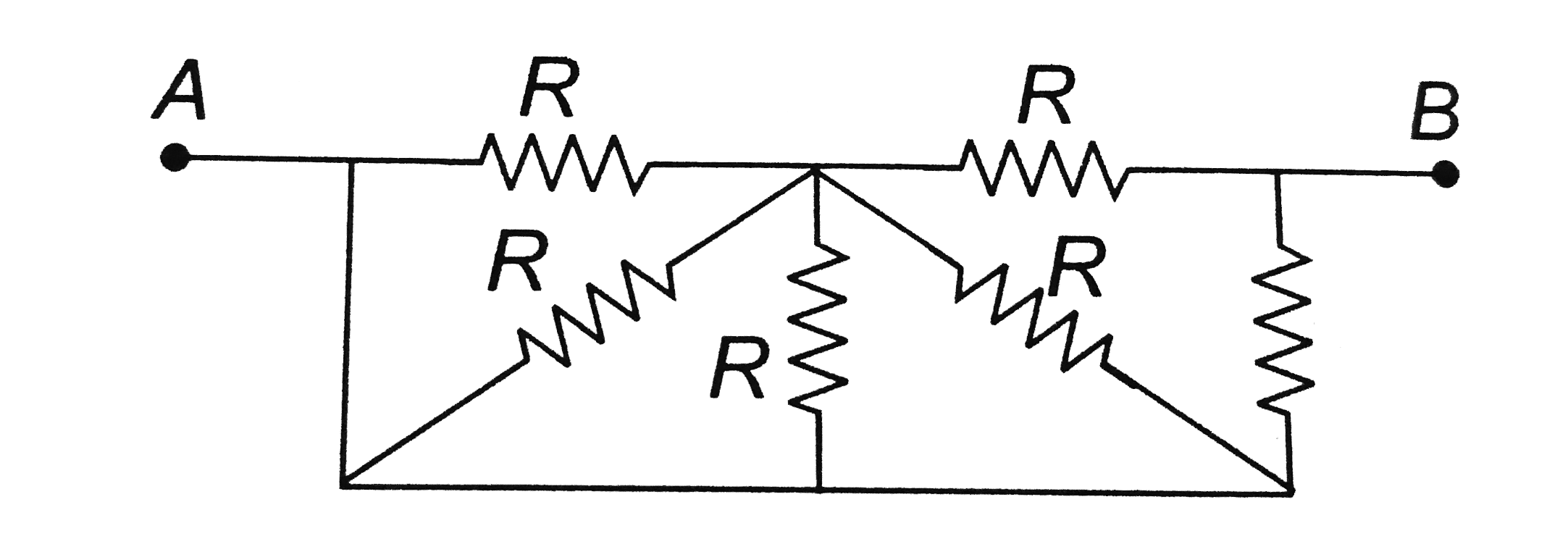
View SolutionThe equivalent resistance between the points A and B is:
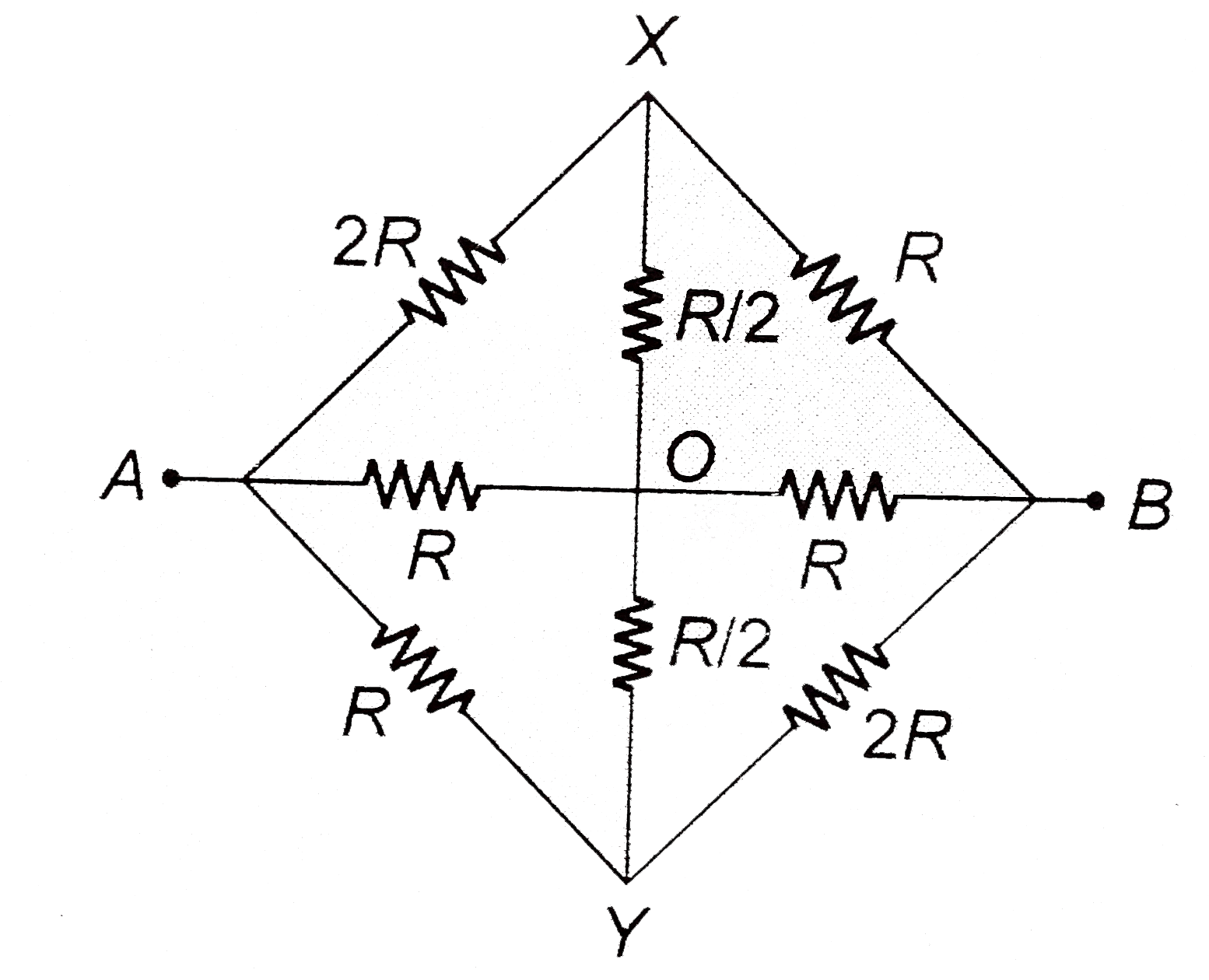
View SolutionThe equivalent resistance between the point A and B is
View Solution

 .
.