A wire of resistance $5.0 Ω$ is used to wind a coil of radius 5 cm. The wire has a diameter 2.0 mm and the specific resistance of its material is $2.0 \times 10^{- 7} Ω m$ . Find the number of turns in the coil.

Video Solution

Text Solution

Verified by Experts

Here, $R = 5.0 Ω, r_{1} = 5 \times 10^{- 2} m$ ,
$D = 2.0 \times 10^{- 3} m, ρ = 2.0 \times 10^{- 7} Ω m$ .
$R = ρ \frac{l}{π D^{2} / 4}$ or $l = \frac{R π D^{2}}{4 ρ}$
Let n be the number of turns in the coil. Then total length of the wire used, $l = 2 π r_{1} n$
or $n = \frac{l}{2} π r_{1} = \frac{R π D^{2}}{4 ρ \times 2 π r_{1}} = \frac{R D^{2}}{8 ρ r_{1}}$
$= \frac{5.0 \times {(2.0 \times 10^{- 3})}^{2}}{8 \times (2.0 \times 10^{- 7}) \times (5 \times 10^{- 2})} = 250$

|

Updated on:21/07/2023

Class 12 PHYSICS CURRENT ELECTRICITY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A wire of resistance $0.5 ω m^{- 1}$ is bent into a circle of radius $1 m$ . The same wire is connected across a diameter $A B$ as shown in fig. The equivalent resistance is

A $π o h m$
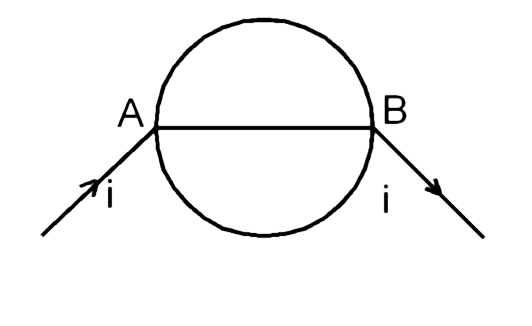B $\frac{π}{(π + 2)} o h m$
C $\frac{π}{(π + 4)} o h m$
D $(π + 1) o h m$
Question 2 - Select One
A wire of resistance $1 Ω$ is stretched so as to change its diameter by $0.25 % .$ The percentage change in its resistance is
A $1.0 %$
B $2.0 %$
C $4.0 %$
D $8.0 %$
Question 3 - Select One
50 turns of a wire of diameter 1mm is wound on a cylinder of radius 5 cm. If the specific resistance of the materical of the wire is $4.5 \times 10^{- 6} Ω m$ , then its resistance is
A $9 k Ω$
B $900 Ω$
C $250 Ω$
D $90 Ω$

PRADEEP-CURRENT ELECTRICITY-Problems for Practice (B)

Home
Ask Doubt
Profile