Let P(r)=QπR4r be the charge density distribution for a solid sphere of radius R and total charge Q. For a point 'p' inside the sphere at distance r1 from the centre of the sphere, the magnitude of electric field is:
Q4π∈0r21
Qr214π∈0R4
Qr213nπ∈0R4
zero
The correct Answer is:C
In Fig, dotted sphere of radius r1 is the Gaussaian surface.According to Gauss's theroem,
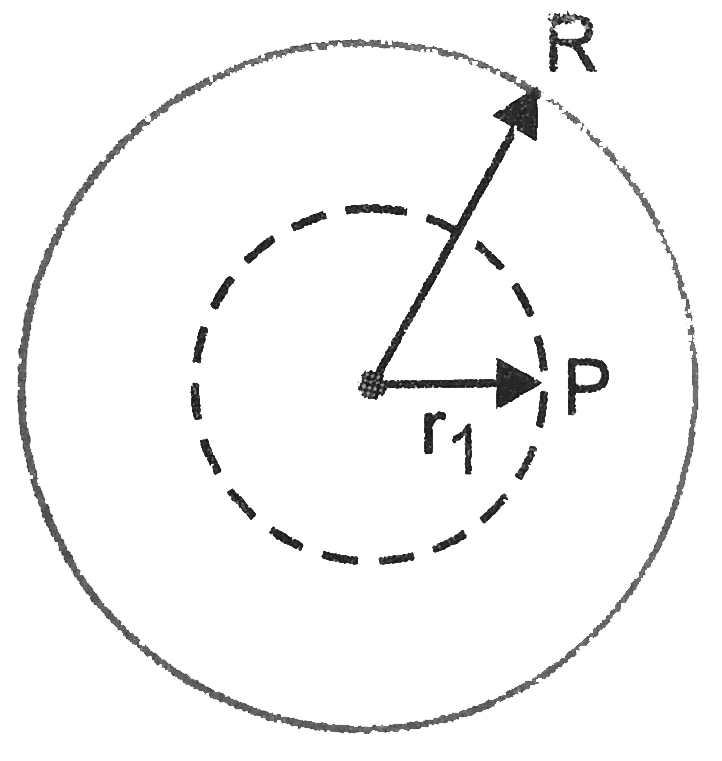
∮→E.d→s=q∈side∈0
Edscos0∘=1∈0ρ(r)×dV
E(4πr21)×1=Qr1∈0πR4(43πr31)
E=Q.4πr413∈0πR4(4πr21)=Qr213π∈0R4
Topper's Solved these Questions
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - FILL IN THE BLANKS
8 Videos
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - PROBLEMS FOR PRACTICE
8 Videos
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - VALUE BASED QUESTIONS
7 Videos
- ELECTRONIC DEVICESBOOK - PRADEEPCHAPTER - ELECTRONIC DEVICESEXERCISE - Fill in the Blanks
1 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Competition Focus (Multiple Choice Questions)
2 Videos
Similar Questions
Let ρ(r)=QrπR4 be the charge density distribution for a solid sphere of radius R and total charge Q. For a point P inside the sphere at a distance r1 from the centre of the sphere, the magnitude of electric field is
View SolutionA hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
View Solution
Knowledge Check
Let ρ(r)=QrπR4 be the charge density distribution for a solid sphere of radius R and total charge Q. For a point P inside the sphere at a distance r1 from the centre of the sphere, the magnitude of electric field is
AQ4πε0r21BQr214πε0R4CQr213πε0R4DzeroLet p(r)=QπR4r be the charge JIR density distribution for a solid sphere of radius R and total charge Q. For a point P inside the sphere at distance z1from the centre of the sphere, the magnitude of electric field is
AQr214πε0R4BQr213πε0R4C0DQ4iε0r21Let ρ(r)=QrπR4 be the charge density distribution for a soild sphere of radius R and total charge Q. For a point P inside the sphere at a distance r1 from the centre of the sphere, the magnitude of electric field is
AQ4πε0r21BQr214πε0R4CQr213πε0R4Dzero
A hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
View SolutionLet p=Qr3πR5 be the volume charge density at distance r from the centre for a a soild sphere of radius R and charge Q. The electric field at r=R2 from the centre will be
View SolutionA sphere of radius R has a charge density σ. The electric intensity at a point at a distance r from its centre is
View SolutionA conducting sphere of radius R is charged to a potential of V volts. Then the electric field at a distance r(>R) from the centre of the sphere would be
View SolutionA conducting sphere of radius R is charged to a potential of V volts. Then the electric field at a distance r(>R) from the centre of the sphere would be
View Solution
