ABCD is a square of side 0.2m. Charges of 2×10−9C,4×10−9Cand8×10−9C are placed at the corners A, B and C respectively. Calculate work required to transfer a charge of 2×10−9C from corner D to centre of the square.
The correct Answer is:6.27×10−7J
To solve the problem of calculating the work required to transfer a charge of 2×10−9C from corner D to the center of the square ABCD, we will follow these steps:
Step 1: Determine the potential at the center of the square (O)
The potential at a point due to a point charge is given by the formula:
V=k⋅Qr
where k=9×109N m2/C2, Q is the charge, and r is the distance from the charge to the point where we are calculating the potential.
For the square ABCD with side 0.2m:
- The distance from each corner (A, B, C) to the center (O) can be calculated using the Pythagorean theorem. Since the center divides the square into two equal halves, the distance r from any corner to the center is:
r=0.2√2=0.1√2m
Now, we calculate the potential at the center (O) due to each charge:
1. Charge at A: Q1=2×10−9C
VA=k⋅Q1r=9×109⋅2×10−90.1√2=18×1000.1√2=180√2V
2. Charge at B: Q2=4×10−9C
VB=k⋅Q2r=9×109⋅4×10−90.1√2=36×1000.1√2=360√2V
3. Charge at C: Q3=8×10−9C
VC=k⋅Q3r=9×109⋅8×10−90.1√2=72×1000.1√2=720√2V
Now, we sum the potentials to find the total potential at the center (O):
VO=VA+VB+VC=180+360+720√2=1260√2≈891.1V
Step 2: Determine the potential at corner D
The potential at corner D is calculated similarly, considering the distances to each charge:
1. Charge at A:
VA=k⋅Q10.2=9×109⋅2×10−90.2=90V
2. Charge at B:
VB=k⋅Q20.2√2=9×109⋅4×10−90.2√2=180√2≈127.3V
3. Charge at C:
VC=k⋅Q30.2=9×109⋅8×10−90.2=360V
Now, we sum the potentials to find the total potential at D:
VD=VA+VB+VC=90+127.3+360≈577.3V
Step 3: Calculate the work done to transfer the charge
The work done W in moving a charge q from a point with potential VD to a point with potential VO is given by:
W=q⋅(VO−VD)
Substituting the values:
W=2×10−9⋅(891.1−577.3)=2×10−9⋅313.8≈6.276×10−7J
Final Answer
The work required to transfer a charge of 2×10−9C from corner D to the center of the square is approximately 6.276×10−7J.
---
The potential at a point due to a point charge is given by the formula:
V=k⋅Qr
where k=9×109N m2/C2, Q is the charge, and r is the distance from the charge to the point where we are calculating the potential.
- The distance from each corner (A, B, C) to the center (O) can be calculated using the Pythagorean theorem. Since the center divides the square into two equal halves, the distance r from any corner to the center is:
r=0.2√2=0.1√2m
1. Charge at A: Q1=2×10−9C
VA=k⋅Q1r=9×109⋅2×10−90.1√2=18×1000.1√2=180√2V
VB=k⋅Q2r=9×109⋅4×10−90.1√2=36×1000.1√2=360√2V
VC=k⋅Q3r=9×109⋅8×10−90.1√2=72×1000.1√2=720√2V
VO=VA+VB+VC=180+360+720√2=1260√2≈891.1V
The potential at corner D is calculated similarly, considering the distances to each charge:
1. Charge at A:
VA=k⋅Q10.2=9×109⋅2×10−90.2=90V
VB=k⋅Q20.2√2=9×109⋅4×10−90.2√2=180√2≈127.3V
VC=k⋅Q30.2=9×109⋅8×10−90.2=360V
VD=VA+VB+VC=90+127.3+360≈577.3V
The work done W in moving a charge q from a point with potential VD to a point with potential VO is given by:
W=q⋅(VO−VD)
Substituting the values:
W=2×10−9⋅(891.1−577.3)=2×10−9⋅313.8≈6.276×10−7J
The work required to transfer a charge of 2×10−9C from corner D to the center of the square is approximately 6.276×10−7J.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - FILL IN THE BLANKS
8 Videos
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - PROBLEMS FOR PRACTICE
8 Videos
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - VALUE BASED QUESTIONS
7 Videos
- ELECTRONIC DEVICESBOOK - PRADEEPCHAPTER - ELECTRONIC DEVICESEXERCISE - Fill in the Blanks
1 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Competition Focus (Multiple Choice Questions)
2 Videos
Similar Questions
ABCD is a square of side 4 cm. Charges of 16×10−9C,−16×10−9C and 32×10−9C are placed at the points A, C and D, respectively. Determine the electric field at point B.
View SolutionABCD is a square of side 0.2 M. Positive charges 2×10−9C,4×10−9C and 8×10−9C are placed at the points A,B and C. Calculate the work done to transfer one columb from D to the centre of the square.
View Solution
Knowledge Check
Calculate the work done in taking a charge −2×10−9C from A to B via C (in diagram )
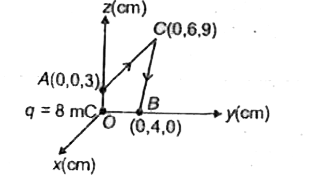 A0.2 jouleB1.2 jouleC2.2 jouleDzero
A0.2 jouleB1.2 jouleC2.2 jouleDzeroFour charges 10−8,−2×108,+3×10−8and2×10−8 coulomb are placed at the four corners of a square of side 1m the potential at the centre of the square is
AzeroB360 voltC180 voltD360√2 voltCharges of +103×10−9C are placed at each of the four corners of a square of side 8cm. The potential at the intersection of the diagonals is
A150√2 voltB1500√2 voltC900√2 voltD900 volt
charges of 20nC each are placed at the corners A and B of a square ABCD of side √8cm and charges of −10nC at the corners C and D. find the potential at the centre of the square.
View SolutionFind the potential at centre of square having charges 2×10−9C,+1×10−9C,−2×10−9Cand3×10−9C at the four corners. The side of the square is √2m.
View SolutionTwo charges +2×10−9C and −8×10−9C are placed 0.3 M apart in air. Find the point or p[oints where the electric field and potential is zero.
View SolutionCharges of +1.0×10−11C,−2.0×10−11,+1.0×10−11C are placed respectively at the corners B, C and D of a rectangle ABCD. Determine the potential at the corner A. given AB=4cm and BC=3cm
View SolutionWhat is the potential at the centre of a square of each side 1.0 meter, when four charges +1×10−8C,−2×10−8C,+3×10−8Cand+2×10−8C are placed at the four corners of the square.
View Solution
