Find the potential at centre of square having charges at the four corners. The side of the square is .
To find the electric potential at the center of a square with given charges at its corners, we can follow these steps:
1. Identify the Charges and Their Positions:
The charges located at the corners of the square are:
- Charge Q1=2×10−9C at corner A
- Charge Q2=1×10−9C at corner B
- Charge Q3=−2×10−9C at corner C
- Charge Q4=3×10−9C at corner D
2. Determine the Side Length of the Square:
The side length of the square is given as √2m.
3. Calculate the Distance from Each Charge to the Center:
The distance from each corner of the square to the center can be calculated using the formula for the diagonal of a square:
d=√(side)2+(side)2=√2⋅(√2)2=√2⋅2=√4=2m
Since the center is equidistant from all corners, the distance R from each charge to the center is:
R=d2=1m
4. Use the Formula for Electric Potential:
The electric potential V at a point due to a point charge is given by:
V=k⋅QR
where k=9×109N m2/C2 is Coulomb's constant.
5. Calculate the Total Potential at the Center:
Since the potential due to each charge adds up, the total potential V at the center is:
V=k(Q1R+Q2R+Q3R+Q4R)
Substituting the values:
V=9×109(2×10−91+1×10−91+−2×10−91+3×10−91)
6. Simplify the Expression:
V=9×109(2×10−9+1×10−9−2×10−9+3×10−9)
=9×109((2−2+1+3)×10−9)
=9×109(4×10−9)
7. Final Calculation:
V=9×4=36Volts
Final Answer:
The potential at the center of the square is 36Volts.
The charges located at the corners of the square are:
- Charge Q1=2×10−9C at corner A
- Charge Q2=1×10−9C at corner B
- Charge Q3=−2×10−9C at corner C
- Charge Q4=3×10−9C at corner D
The side length of the square is given as √2m.
The distance from each corner of the square to the center can be calculated using the formula for the diagonal of a square:
d=√(side)2+(side)2=√2⋅(√2)2=√2⋅2=√4=2m
Since the center is equidistant from all corners, the distance R from each charge to the center is:
R=d2=1m
The electric potential V at a point due to a point charge is given by:
V=k⋅QR
where k=9×109N m2/C2 is Coulomb's constant.
Since the potential due to each charge adds up, the total potential V at the center is:
V=k(Q1R+Q2R+Q3R+Q4R)
Substituting the values:
V=9×109(2×10−91+1×10−91+−2×10−91+3×10−91)
V=9×109(2×10−9+1×10−9−2×10−9+3×10−9)
=9×109((2−2+1+3)×10−9)
=9×109(4×10−9)
V=9×4=36Volts
The potential at the center of the square is 36Volts.
Topper's Solved these Questions
- ELECTRIC POTENTIAL AND ELECTRIC FLUXBook:SL ARORAChapter:ELECTRIC POTENTIAL AND ELECTRIC FLUXExercise:Problem
Explore 15 Videos
- ELECTRIC POTENTIAL AND ELECTRIC FLUXBook:SL ARORAChapter:ELECTRIC POTENTIAL AND ELECTRIC FLUXExercise:Problems for self practive
Explore 61 Videos
- CURRENT ELECTRICITYBook:SL ARORAChapter:CURRENT ELECTRICITYExercise:Problems For Self
Explore 101 Videos
- ELECTRICAL INSTRUMENTSBook:SL ARORAChapter:ELECTRICAL INSTRUMENTSExercise:Problem for self practice
Explore 81 Videos
Similar Questions
Knowledge Check
A square of side 20 cm is enclosed by a surface of sphere of 80 cm radius. Square and sphere have the same centre. Four charges +4×10−6C,
−5×10−6C,−3×10−6C,+6×10−6C are located at the four corners of a square then total flux from spherical surface in N−m2C−1 will beAzeroB48π×103C72π×103D36π×103A square of side 20cm. Is enclosed by a surface of sphere of 80 cm. radius . Square and sphere have the same centre. Four charges +2×10−6c,−5×10−6c,−3×10−6c,+6×10−6c are located at the four corners of a square, Then out going total flux from spherical surface in N−m3/c will be
AzeroB(16π)×10−6C(8π)×10−6D(36π)×10−6Four charge q1=2×10−8C,q2=−2×10−8C,q3=−3×10−8C, and q4=6×10−8C are palced at four corners of a square of side √2m. What is the potential at the centre of the square?
A270VB300VCZeroD100V
Four point charges q1,q2,q3 and q4 are placed at the corners of the squares of side a,as shown in figure.Calculate the potential at the centre of the square.
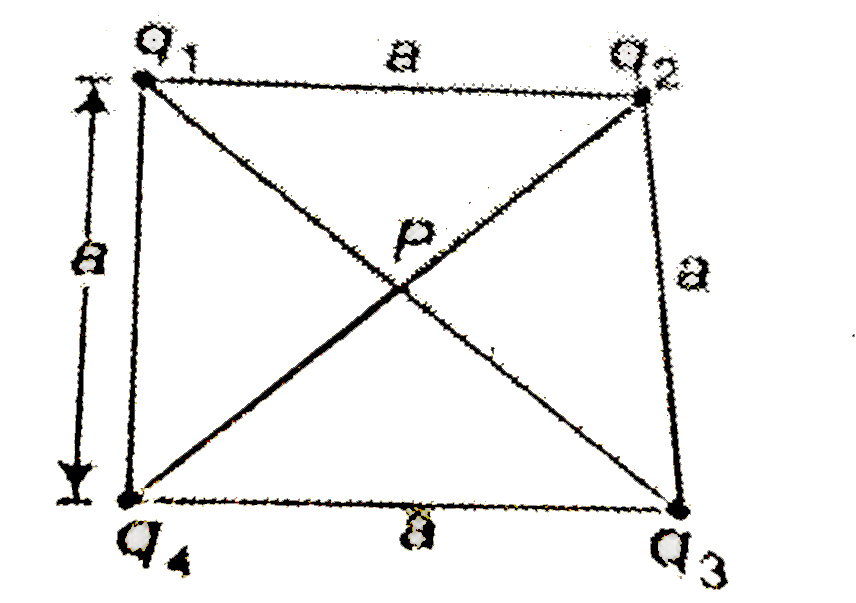
(Given, q1=1×10−8C,q2=−2×10−8C,q3=3×10−8C,q4=2×10−8C and a=1m)
View SolutionABCD is a square of side 4 cm. Charges of 16×10−9C,−16×10−9C and 32×10−9C are placed at the points A, C and D, respectively. Determine the electric field at point B.
View SolutionFour charges q1=2×10−8C,q2=−2×10−8C,q3=−3×10−8C and q4=6×10−5C are placed at four corners of a square of side √2m. What is the potential at the centre of the square ?
View SolutionFour charges q1=2×10−8C,q2=−2×10−8C,q3=−3×10−8C and q4=6×10−5C are placed at four corners of a square of side √2m. What is the potential at the centre of the square ?
View SolutionFour charges 10−8,−2×108,+3×10−8and2×10−8 coulomb are placed at the four corners of a square of side 1m the potential at the centre of the square is
View Solution

