A pair of stars rotates about a common centre of mass. One of the stars has a mass M and the other m. Their centres are a distance d apart, d being large compared to the size of either star. Derive an expression for the period of revolution of the stars about their common centre of mass. Compare their angular momenta and kinetic energies.
The correct Answer is:(a)T=2πd3/2√3Gm,(b)2,(c)2
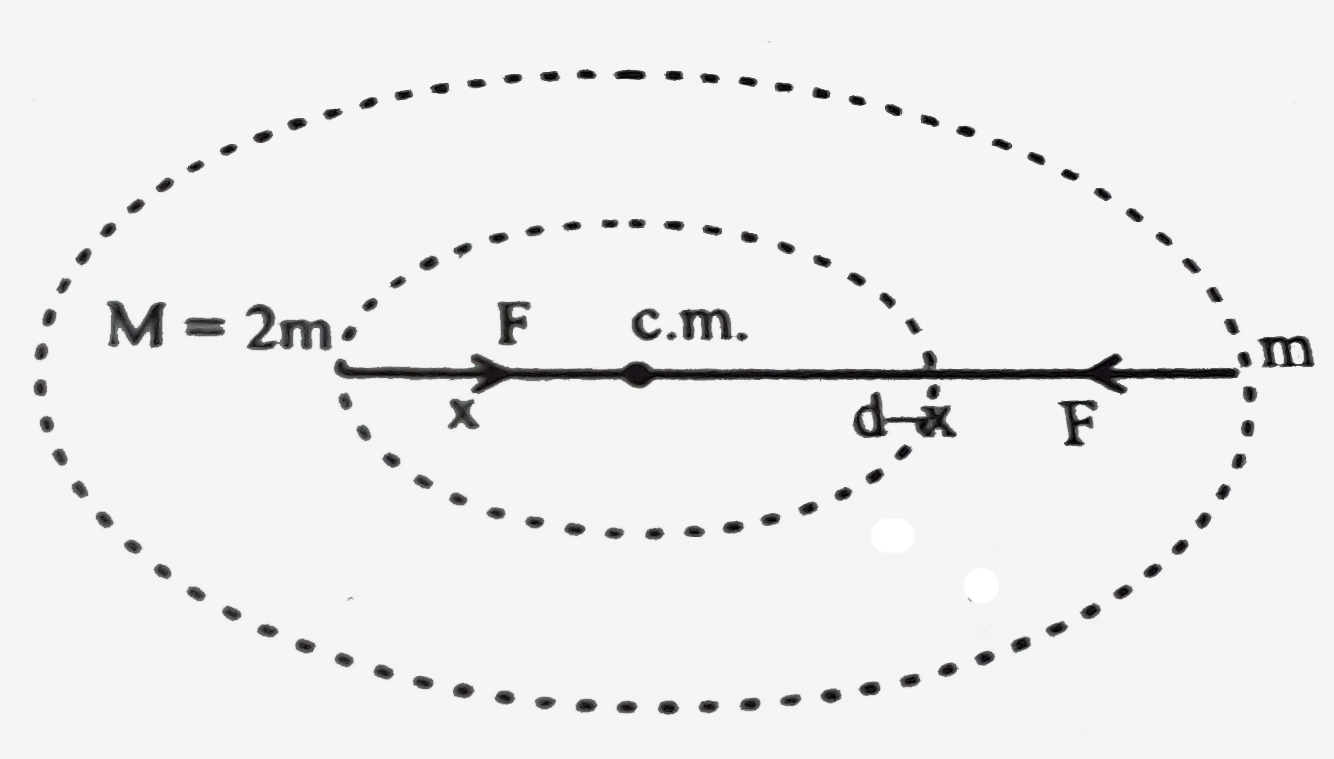
They will rotate about their c.m.
position of centre of mass
0=2m(−x)+m(d−x)2m+m⇒x=d3
(a) These force of atraction will provided required centripetal force
(2m)v2Md/3=G2m.md2⇒vM=√R3GMd
T=2π(d/3)vM⇒T=2πd3.√3dGM
T=2π√d33GM⇒T=2πd3/2√3GM
Similar Questions
A pair of stars rotates about a common centre of mass. One of the stars has a mass M which is twice as large as the mass m of the other. Their centres are a distance apart, d being compared to the size of either star.
(a) Derive an expression for the period of rotation of the stars about their common centre of mass in terms of d, m, G.
(b) Compare the angular momentum of the two stars about their common centre of mass by calculating the ratio Lm/LM.
(c ) Compare the kinetic energies of the two stars by calculating th eratio Km/KM.
View SolutionIn a double star, two stars (one of mass m and the other of mass 2m) distance d apart rotate about their common centre of mass., Deduce an expressioin for the period of revolution. Show that te ratio of their angular momenta about the centre of mass is the same as the ratio of their kinetic energies.
View Solution
Knowledge Check
A pair of stars rotates about their centre of mass One of the stars has a mass M and the other has mass m such that M=2m The distance between the centres of the stars is d (d being large compared to the size of either star) .
The period of rotation of the stars about their common centre of mass (in time of d ,m ,G) is .A√4π2Gmd3B√8π2Gmd3C√2π23Gmd3D√4π23Gmd3A pair of stars rotates about their centre of mass One of the stars has a mass M and the other has mass m such that M=2m The distance between the centres of the stars is d (d being large compared to the size of either star) .
The period of rotation of the stars about their common centre of mass (in time of d ,m ,G) is .A√4π2GMd3B√8π2GMd3C√2π23GMd3D√4π23GMd3A pair of stars rotates about their centre of mass One of the stars has a mass M and the other has mass m such that M=2m The distance between the centres of the stars is d (d being large compared to the size of either star) .
The ratio of the angular momentum of the two stars about their common centre of mass (Lm/Lm) is .A1B2C4D9
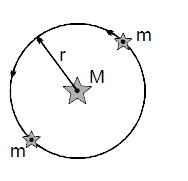
A certain triple-star system consists of two stars, each of mass m, revolving about a central star, mass M, in the same circular orbit. The two stars stay at opposite ends of a diameter of the circular orbit, see figure. Derive an expression for the period of revolution of the stars, the radius of the orbit is r.
View SolutionA pair of stars rotates about their centre of mass One of the stars has a mass M and the other has mass m such that M=2m The distance between the centres of the stars is d (d being large compared to the size of either star) .
The ratio of kinetic energies of the two stars (Km/KM) is .
View SolutionIn a binary star system one star has thrice the mass of other. The stars rotate about their common centre of mass then :
View SolutionA binary star system consists of two stars. One star has twice the mass of the other. The star rotates about their common centre of mass. Which of the following statement is correct?
View SolutionIn a binary star system one of the stars has mass equal to mass of sun (M). Separation between the stars is four times the average separation between earth and sun. Mass of the other star so that time period of revolution of the stars each other is equal to one earth year is
View Solution