STATEMENT-1 : The height of a liquid column in a U-tube is 0.3m. If the liquid in one of the limbs is depressed, and then released, the time period of liquid column will be 1.1sec.
STATEMENT-2 : this follows from the relation.
T=2π√hg
Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1.
Statement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-1.
Statement-1 is True, Statement-2 is False.
Statement-1 is False, Statement-2 is True.
The correct Answer is:A
Step by step video, text & image solution for STATEMENT-1 : The height of a liquid column in a U-tube is 0.3 m. If the liquid in one of the limbs is depressed, and then released, the time period of liquid column will be 1.1 sec. STATEMENT-2 : this follows from the relation. T = 2pisqrt(h)/(g) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
A uniform U-tube contains a very slightly mobile liquid to a height of 50 cm in each limb. If the liquid in one lime is depressed and then released, find the period of oscialltion of the liquid in the tube.
View SolutionA vertical U-tube contains liquid of uniform density upto a height of 3 cm. If the liquid in one arm is depressed and then released, it performs S.H.M. in the tube. Calculate its time period of oscillations.
Assume U-tube to be of uniform cross section.
Take, g = 980 cm/s2
View Solution
Knowledge Check
A vertical U−tube contains a liquid. The total length of the liquid column inside the tibe is 1. When the liquid is in equilibrium, the liquid surface in one of the arms of the U−tube is pushed down slightly and released. The entire liquid column will undergo a periodic motion.
AThe motion is not simple harmonic motionBThe motion is simple harmonic motionCIf it undergoes simple harmonic motion, the time period will be 2π√l/g.DIf it undergoes simple harmonic motion, the time period will be 2π√l/2g.The rise of liquid into capillary tube is h1. If the apparatus is taken in a lift moving up with acceleration the height is h2 then
Ah1=h2Bh1>h2Ch2>h1Dh2=0The height of liquid column in capillary tube is h the radius of capillary tube is r.ρ is the density of liquid , g is acceleration due to gravity and θ is angle of contact . The surface tension of the liquid is ,
At=rhρg2cosθBT=2cosθhρgrCT=2cosθrρhgDall of these
The ratio of height of a mercury column in a barometer at a place to the height of the liquid column at the same place are 1:4. Find the density of the liquid.
View SolutionA vertical U tube contains a liquid of density ρ, length of the liquid in the tube is 2H. The liquid is displaced slightly and released. Show that the liquid will execute SHM. Also find its time period. Take liquid to be ideal.

View SolutionA vertical U-tube has two liquids 1 and 2. The heights of liquids columns in both the limbs are h and 2h, as shown in the figure. If the density of the liquid 1 is 2ρ.
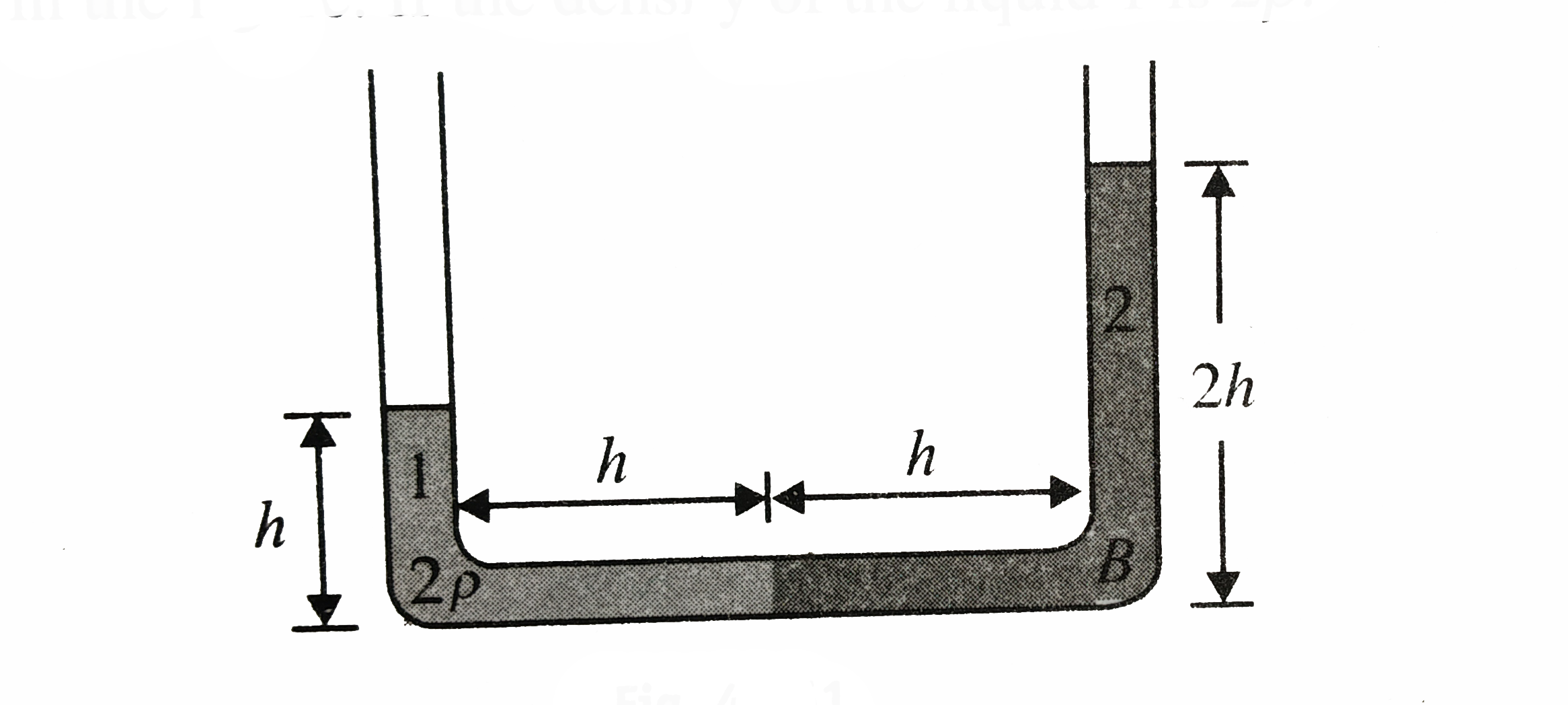
a. Find the density of liquid 2.
b. If we accelerate the tube towards right till the heights of liquid columns will be the same, find the acceleration of the tube.
View SolutionA vertical U-tube has a liquid up to a height h. If the tube is slowly rotated to an angular speed ω=√gh find the (i) heights of the liquid column, ii pressures at the points 1,2 and 3 in the limbs in steady state.

View SolutionA U-tube filled with a liquid of volumetric expansion coefficient 10−5/∘C lies in a vertical plane. The height of liquid column in the left vertical limb is 100 cm. The liquid in the left vertical limb is maintained at a temperature =∘C while the liquid in the right limb is maintained at a temperature =100∘ C The difference in levels in the two limbs is
View Solution
