A man is swinging on a swing made of 2 ropes of equal length L and in direction perpendicular to the plane of paper. The time period of the small oscillations about the mean position is
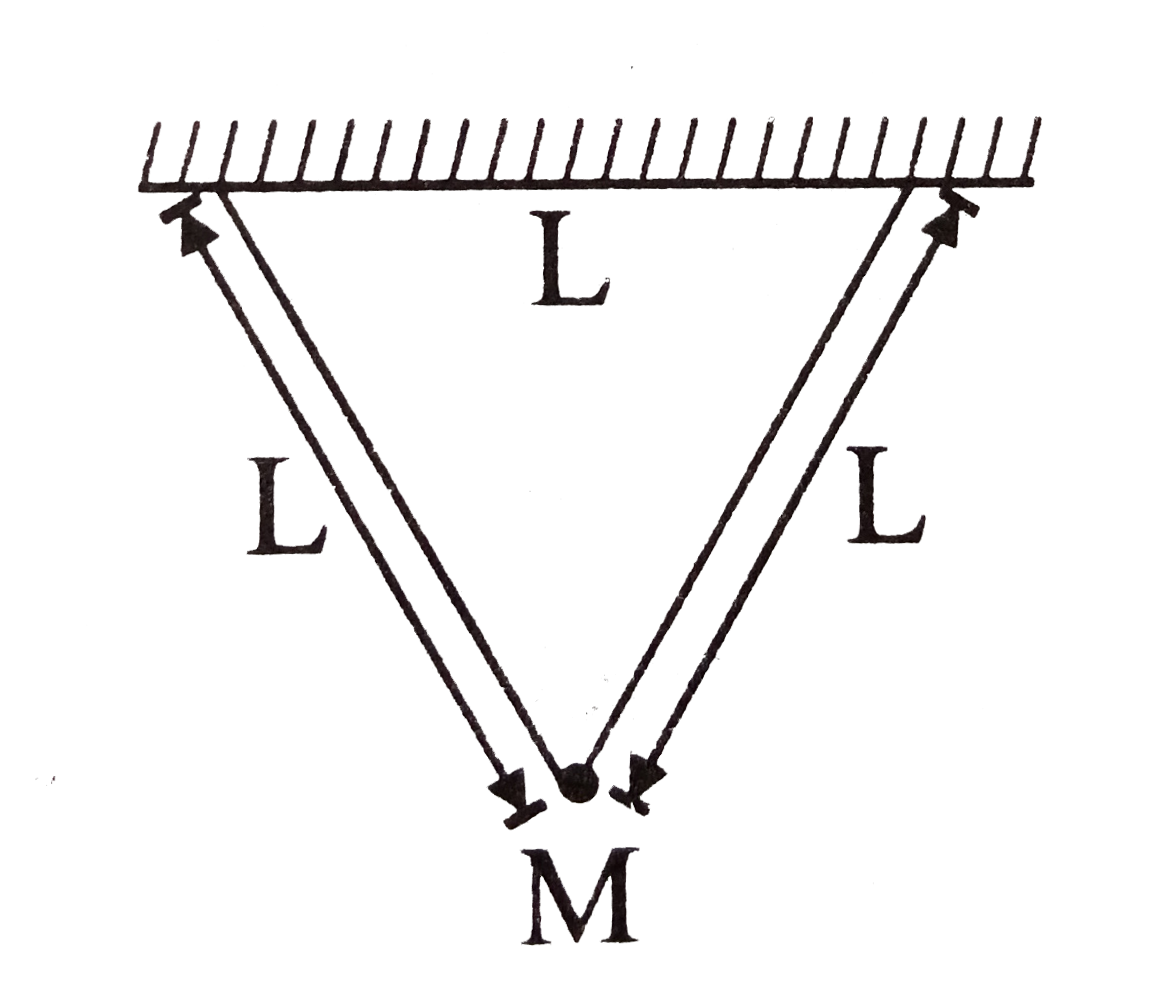
2π√L2g
2π√√3L2g
2π√L2√3g
π√Lg
The correct Answer is:B
Figure
Similar Questions
A weightless rigid rod with a load at the end is hinged at point A to the wall so that it can rotate in all directions (Fig).
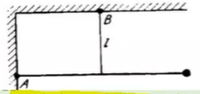
The rod is kept in the horizontal position by a vertical inextensible thread of length 1, fixed at its midpoint. The load receives a momentum in the direction perpendicular to the plane of the figure.
Determine the period T of small oscillations of the system.
View SolutionA simple pendulum is suspnded from the ceilignof a car accelerating uniformly on a horizontal road.If the acceleration is a0 and the length of the pendulum is l, find the time period of small oscillations about the mean position.
View Solution
Knowledge Check
A uniform stick of length l is mounted so as to rotate about a horizontal axis perpendicular to the stick and at a distance d from the centre of mass. The time period of small oscillation has a minimum value when d/l is
A1√2B1√12C1√3D1√6A disc of radius R is pivoted at its rim. The period for small oscillations about an axis perpendicular to the plane of disc is
A2π√RgB2π√2RgC2π√2π3gD2π√3R2gThe potential energy of a peticle of mass 'm' situated in a unidimensional potential field varies as U(x)=0[1−cosax], where U0 and a are constants. The time period of small oscillations of the particle about the mean positions is :
A2π√maU0B2π√amU0C2π√ma2U0D2π√32mU0
Consider a physical pendulum consisting of an inverted T shaped rigid body made out, of two identical, thin, uniform rods of mass M and Iength L each joined together and hinged at the top point as shown, free to rotate in a vertical plane about an axis perpendicular to the plane of the figure, the time period for 'small' angular'oscillations is T=2π√αLβg. Find |α−β|.
'(##CEN_KSR_PHY_JEE_C16_E01_034_Q18##)'
View SolutionA square plate of mass M and side length L is hinged at one of its vertex (A) and is free to rotate about it. Find the time period of small oscillations if
(a) the plate performs oscillations in the vertical plane of the figure. (Axis is perpendicular to figure.)
(b) the plate performs oscillations about a horizontal axis passing through A lying in the plane of the figure.

View SolutionA small particle is tied by the help of two strings to vertical walls with the parameters as shown in the figure (g=π2). The time period of the small oscillations of the particle if it is displaced perpendicular to the plane of the paper slightly is x sec, the value of x is ____________
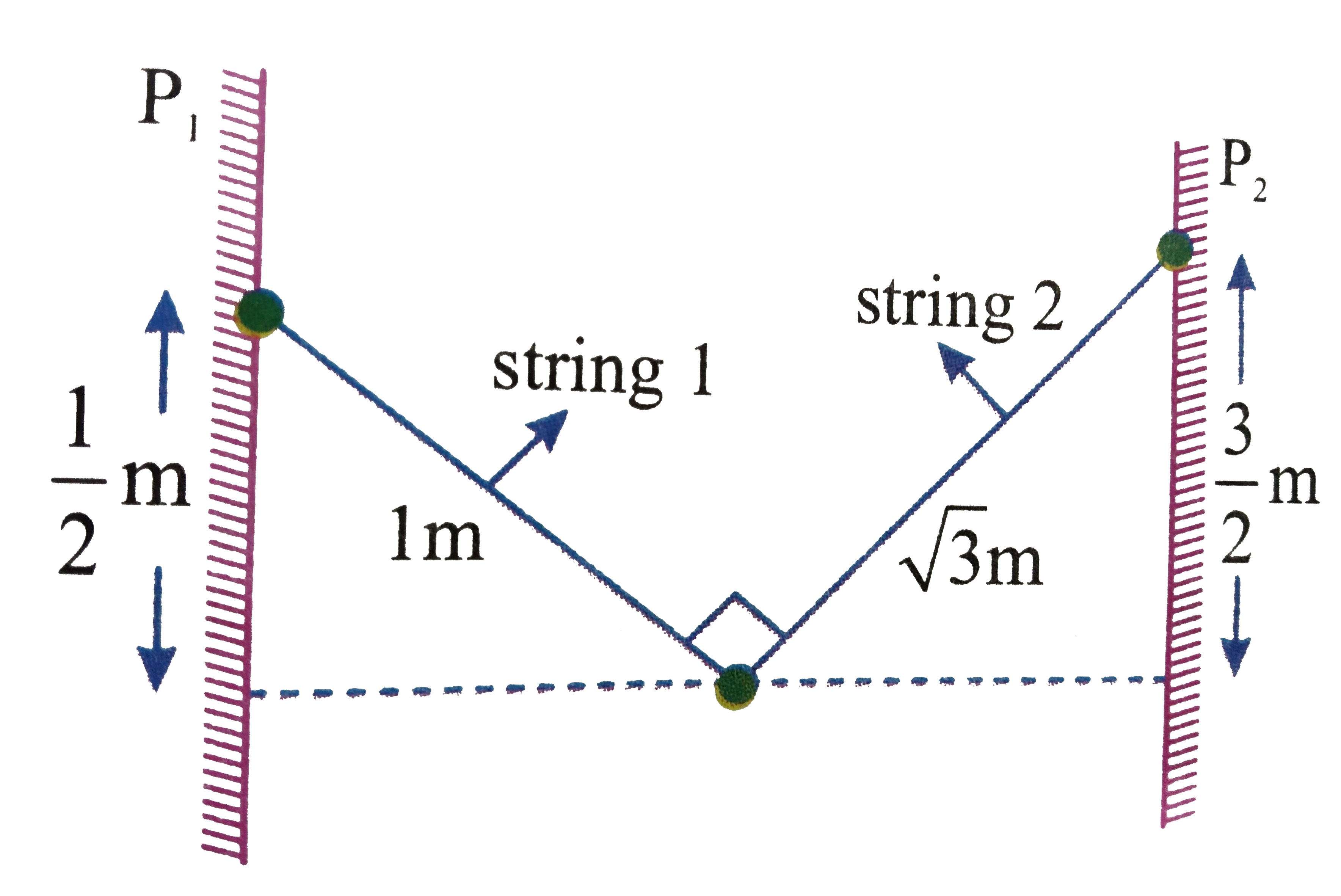
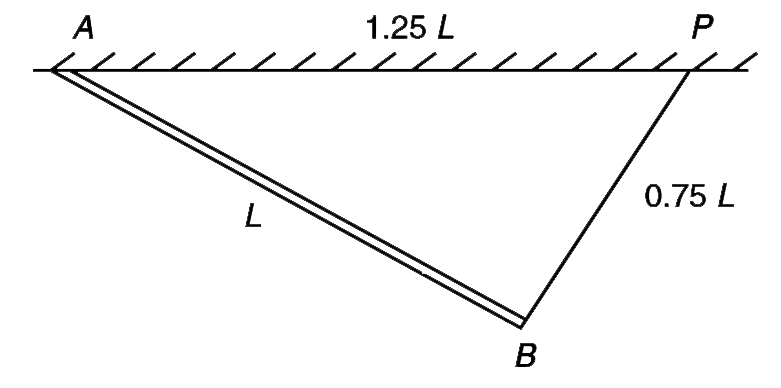
View SolutionA uniform rod AB of mass m and length L is tied, at its end B, to a thread which is attached to point P on the ceiling. Length of the thread PB is 0.75 L. The other end A of the rod is hinged at a point on the ceiling. Distance AP = 1.25 L. End B of the rod is pushed gently perpendicular to the plane of the figure and it starts oscillating
(a) Find the moment of inertia of the rod about line AP.
(b) Assuming that the triangle APB makes a small angle θ with the vertical plane, write the restoring torque acting on the rod.
(c ) Calculate the time period of small oscillations.
View SolutionThe potential energy of a peticle of mass 'm' situated in a unidimensional potential field varies as U(x)=0[1−cosax], where U0 and a are constants. The time period of small oscillations of the particle about the mean positions is :
View Solution
