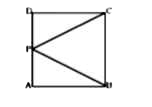
For the given uniform square lamina ABCD, whose centre is O,
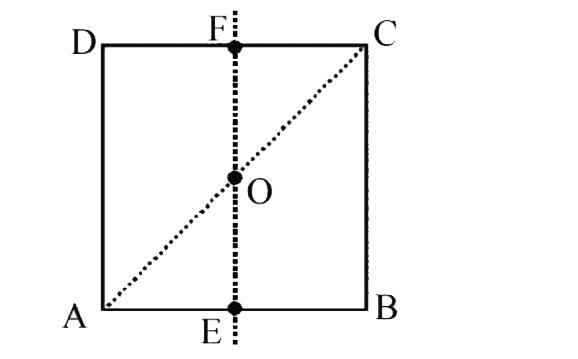
IAC=√2IEF
√2IAC=IEF
IAD=3IEF
IAC=IEF
The correct Answer is:D
IAC=12(Ml26)=Ml212,IEF=Ml212,IAC=IEF
Similar Questions
For the given uniform square lamina ABCD, where centre is O. Its moment of inertia about an axis AD is equal to how many times its moment of inertia about an axis EF?
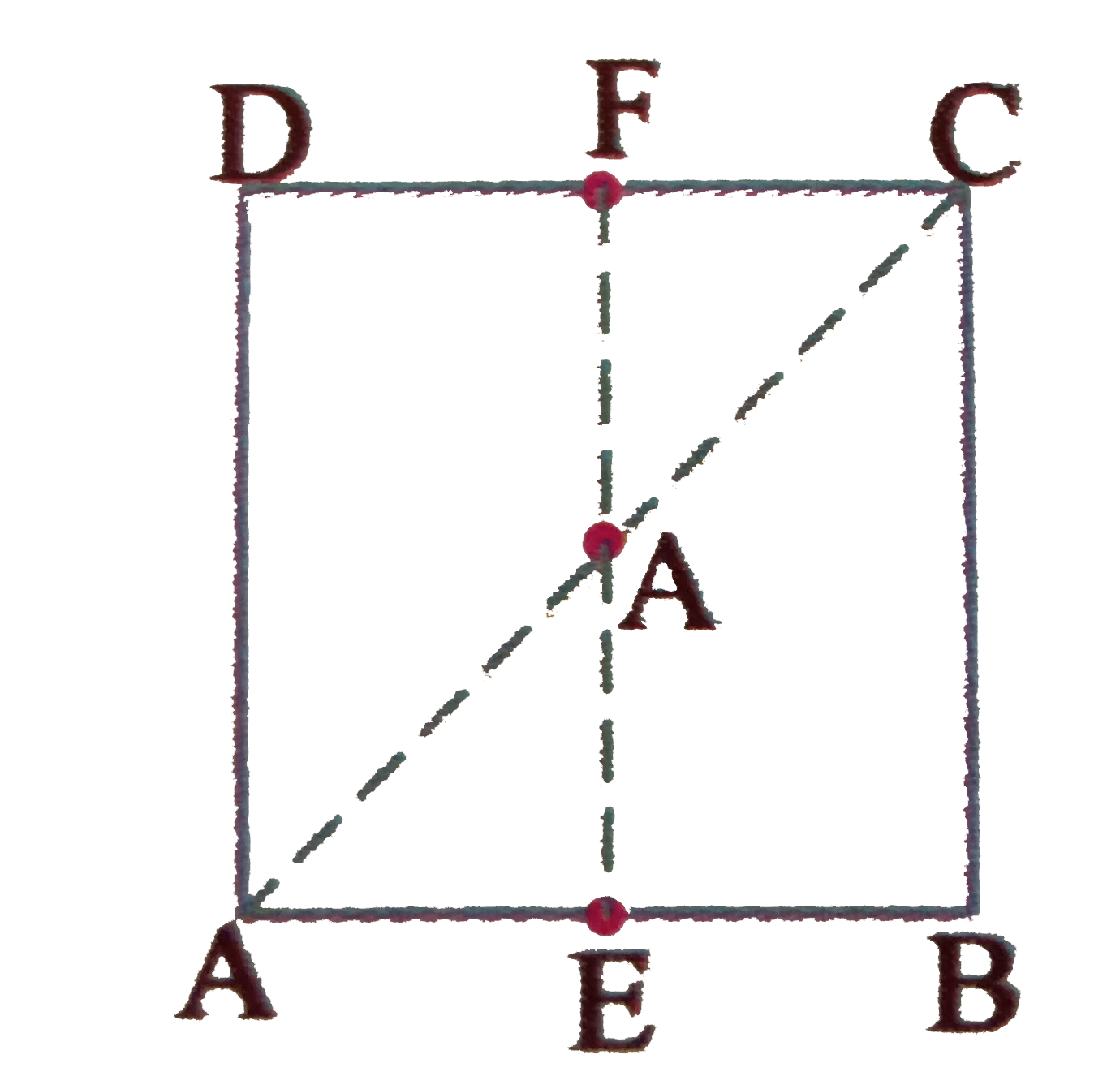
1√2IAC=IEF 2.IAD=3IEF
3.IAC=4IEF. 4.IAC=√2IEF
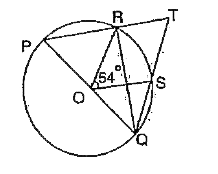
View SolutionPQ is the diameter of the given circle, whose centre is O. Given, ∠Ros=54∘, calculate ∠RTS.
View Solution
Knowledge Check
In the adjoining diagram ABCD is a square with side 'a' cm. In the diagram the area of the larger circle with centre 'O' is equal to the sum of the areas of all the rest four circles with equal radii, whose centres are P,Q,R and S . What is the ratio between the side of square and radius of a smaller circle ?
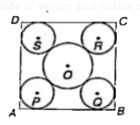 A(2√2+3)B(2+3√2)C(4+3√2)Dcan't be determined
A(2√2+3)B(2+3√2)C(4+3√2)Dcan't be determinedIn the given figure, ABCD is a square whose side is 4 cm. P is a point on the side AD. What is the minimum value (in cm) of BP+CP?
 A4√5B4√4C6√3D4√6
A4√5B4√4C6√3D4√6
In the given figure, side of square ABCD is 7 cm. With centre D and radius DA, sector D-AXC is drawn. find out the area of the shaded ragion.
View SolutionThere is a pentagon ABCDE, whose centre is O. Five identical charges Q are placed at the corners of pentagon.
(a)What will be the net electric field intensity at the centre of pentagon ?
(b)If charge at corner A is moved to centre O of pentagon, then what will be the net force experienced by it ?
Distance of any vertex of pentagon from its centre is d.

View SolutionIn the given figure, OPOR is a square. A circle drawn with centre O, cuts the square X and Y. Prove that QX=QY.
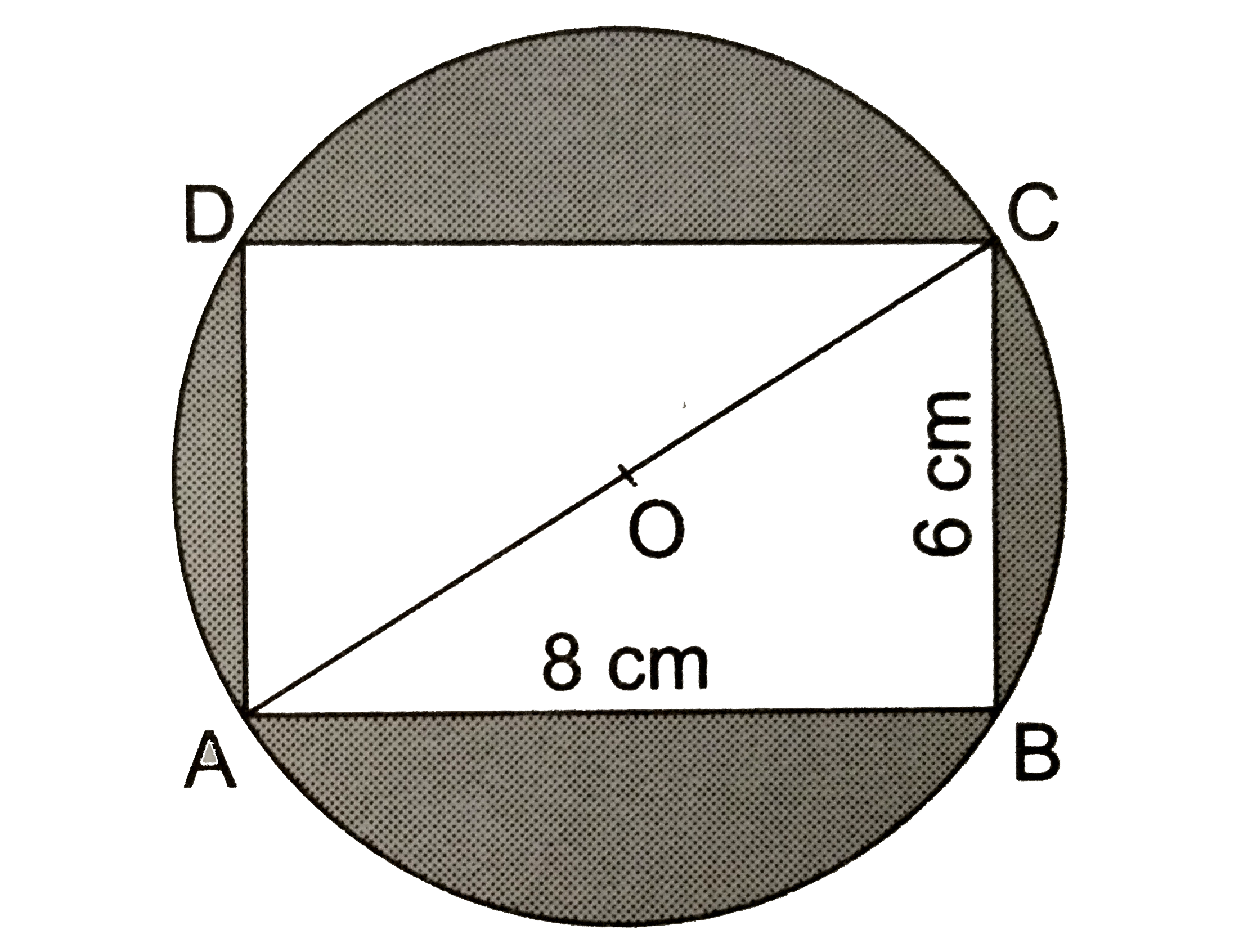
View SolutionFind the area of the shaded region in the given figure, if ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of the circle.
View SolutionIn the given figure, ABCD is a square whose side is 4 cm. P is a point on the side AD. What is the minimum value (in cm) of BP+CP?

View SolutionIn the given figure ABCD is a square each of whose sides measures 28 cm. Find the area of the shaded region. [Take π=227]

View Solution
