A child with mass m is standing at the edge of a disc with moment of inertia I, radius Rm and initial angular velocity ω. See figure given below. The chlid jumps off the edge of the disc with tangential velocity v with respect to the ground. The new angular velocity of the disc is.
 .
.
√Iω2−mv2I
√(I+mR2)ω2−mv2I
Iω−mvRI
(I+mR2)ω−mvRI
The correct Answer is:D
From conservation of linear momentum
(I+mR2)ω=mvR+Iω'
ω'(I+mR2)ω−mvRI.
Similar Questions
A person of mass m stands at the edge of a circular platform of radius R and moment of inertia. A platform is at rest initially. But the platform rotate when the person jumps off from the platform tangentially with velocity u with respect to platfrom. Determine the angular velocity of the platform.
View SolutionA disc of mass M and radius r is rotating with an angular velocity ω. If gently, two masses m each are placed at a distance r/2 on either side of the axis of rotation, what will be the new angular velocity ?
View Solution
Knowledge Check

A child with mass m is standing at the edge of a merry go round having moment of inertia I, radius R and initial angular velocity ω as shown in the figure. The child jumps off the edge of the merry go round with tangential velocity v with respect to the ground. The new angular velocity of the merry go round isA√Iω2−mv2IB√(I+mR2)ω2−mv2ICIω−mvRID(I+mR2)ω−mvRIThe angular momentum of a body with mass (m) moment of inertia (I) and angular velocity (ω) rad/s is equal to
AIωBIω2CIωD1ω2A uniform circular disc of radius R is rotating about its own axis with moment of inertia I at an angular velocity ω if a denser particle of mass m is gently attached to the rim of disc than its angular velocity is
AωBIω(I+mR)CI+mR2IωDIωI+mR2
A insect of mass m stands on a horizontal disc platform of moment of inertia 1 which is at rest. What is the angular velocity of the disc platform when the insect goes along a circle of radius r, concentric with the disc, with velocity v relative to the disc.
View SolutionA child of mass m is standing, on the periphery of a circular platform of radius R, which can rotate about its central axis. The moment of inertia of the platform is I. Child jumps off from the platform with a velocity u tangentially relative to the platform. Find the angular speed of the platform after the child jumps off.
View SolutionA disc of mass M and radius R is rotating about its axis with initial angular velocity of ω0 as shown. Now two small masses of m each one kept on the circumference diametrically opposite to eachother. Find new angular velocity
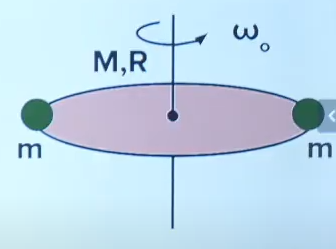
View SolutionA circular disc of mass M and radius R is rotating with angular velocity ω . If two small spheres each of mass m are gently attached to two diametrically opposite points on the edge of the disc, then the new angular velocity of the disc will be
View SolutionInitial angular velocity of a circualr disc of mass M is ω1. The tow sphere of mass ma re attached gently to diametrically opposite points ont eh edge of the disc. What is the final angular velocity on the disc?
View Solution

