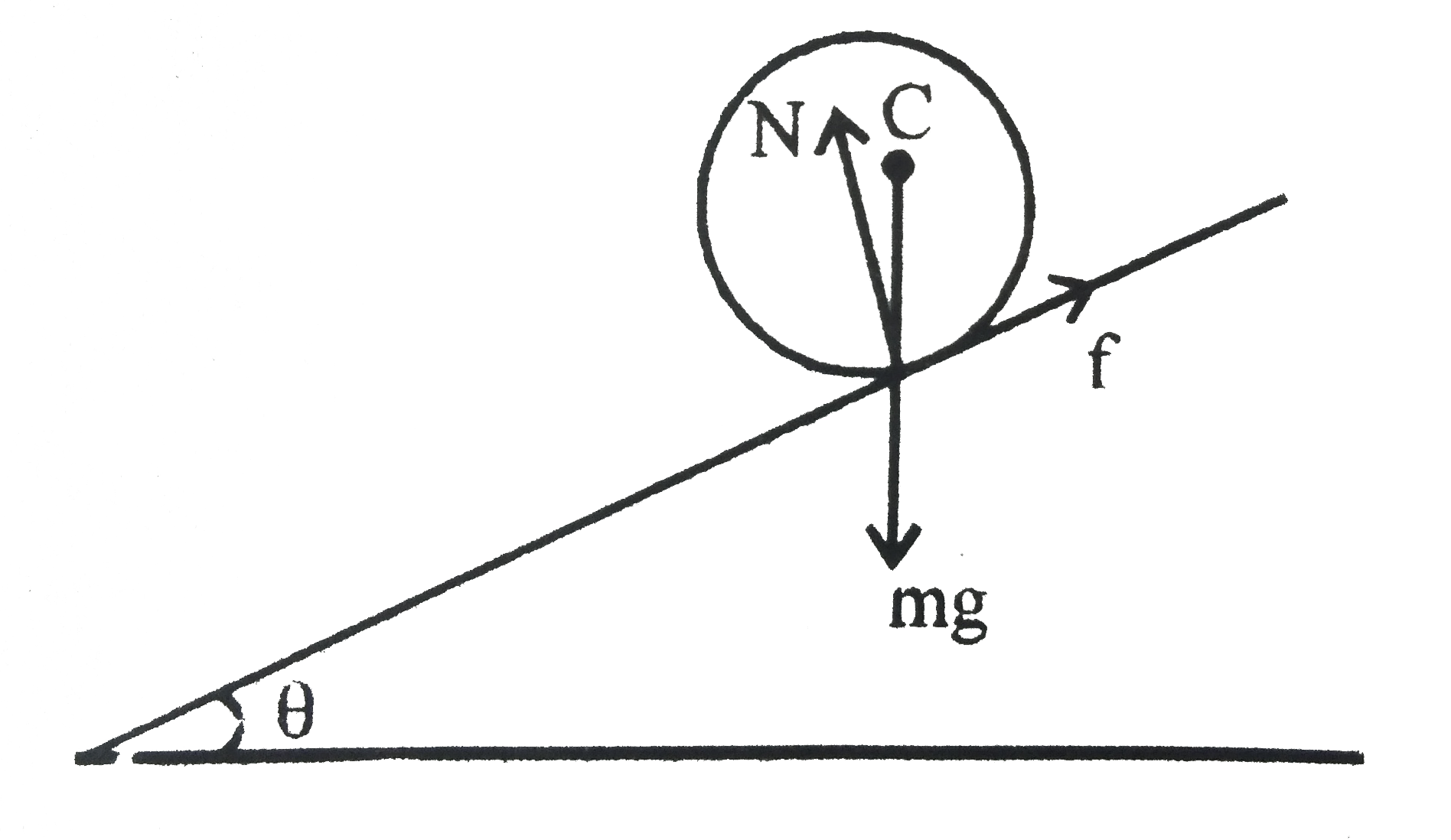
A non uniform sphere can be kept on a rough inclined plane so that it is in equilibrium. In the figure below the dots representsm location of centre of mass. In which one of the positions can sphere be in equilibrium ?

The correct Answer is:C
Since sphere is in equilibrihm net torque about point of of contact must be zero for that line of action of mg must pass through point of contact.
 .
.
Similar Questions
Knowledge Check

A sphere kept on a rough inclined plane is in equilibrium by a string wrapped over it. If angle of inclination is θ, the tension in string will be equal toAmgsinθB2mgsinθCmgsinθ2DmgcosθFind minimum height of the obstacle so that the sphere can stay in equilibrium
 AR1+cosθBR1+sinθCR(1−sinθ)DR(1−cosθ)
AR1+cosθBR1+sinθCR(1−sinθ)DR(1−cosθ)A hollow spherre is released from rest on a rough inclined plane as shown in the figure. Find the velocity of point of contact as a function of time. ( m = mass of hollow sphere, R = radius of sphere )
 A2tB4tC6tD8t
A2tB4tC6tD8t
A mass of 100kg is resting on a rough inclined plane of angle 30∘ If the coefficient of friction is 1/√3 find the greatest and the least forces that acting parallel to the plane in both cases just maintain the mass in equilibrium .
View SolutionA block having equilateral triangular cross-section of side a and mass m is placed on a rough inclined surface, so that it remains in equilibrium as shown in figure. The torque of normal force acting on the block about its centre of mass is

View SolutionA sphere of weight W=100N is kept stationary on a rough inclined plane by a horizontal string AB as shown in figure. Then :

View SolutionA uniform solid sphere rolls up (witout slipping) the fixed inclined plane, and then back down. Which is the correct graph of acceleration a of centre of mass of solid sphere as function of time t (for the duration sphere is on the incline)? Assume that the sphere rolling up has a positive velocity.
View SolutionA sphere and circular disc of same mass and radius are allowed to roll down an inclined plane from the same height without slipping. Find the ratio of times taken by these two to come to the bottom of incline :
View Solution