The velocities of A and B shown in fig. Find the speed (in ms−1) of block C. (Assume that the pulleys and string are ideal).

The correct Answer is:5m/s
By constrained equaiton for length
l1+l2+l3+l4= constant
dl1dt+dl2dt+dl3dt+dl4dt=0…(1)
since dl1dt=dl2dt=vA=vB=1−3=−2m/s&dl3dt=0
putting the value in eq.(1)
−2+(−2)+0+dl4dt=0
dl4dT=4m/s==⇒vCB=4m/s→vCB=→vC−→vB==⇒→vC=→vCB+→vB
vC=√v2CB+v2B⇒vC=√32+42
⇒vC=5m/s
Similar Questions
The block Q moves to the right with a constant velocity v0 as shown in figure. The relatives velocity of body P with respect to Q is ( assume all pulleys and strings are ideal)
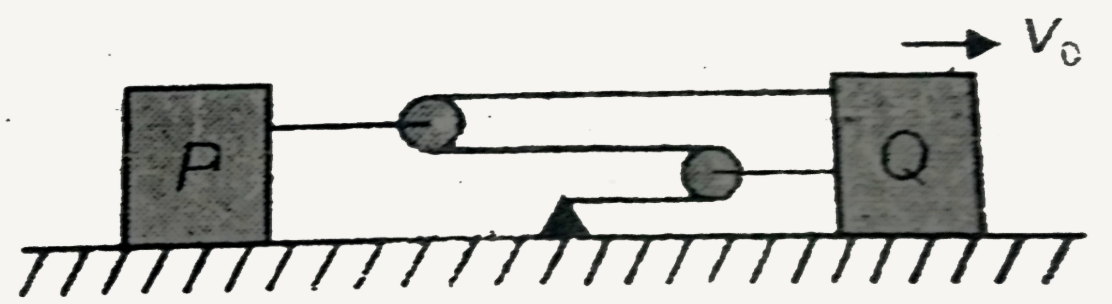
View SolutionIn the figure-2.205 shown in blocks A, B and C has masses mA=5kg,mB=5kg and mC=10kg respectively, find the acceleration of the three blocks. Assume all pulleys and strings are ideal. (Take g=10m/s2)
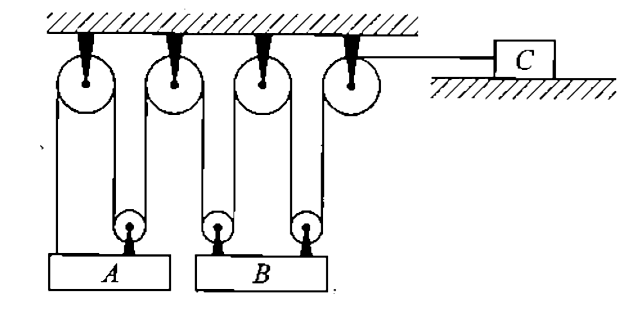
View Solution
Knowledge Check
The velocities of A and B are marked in the figure-1.130. The velocity of block C is (assume that the pulleys are ideal and string inextensible) :
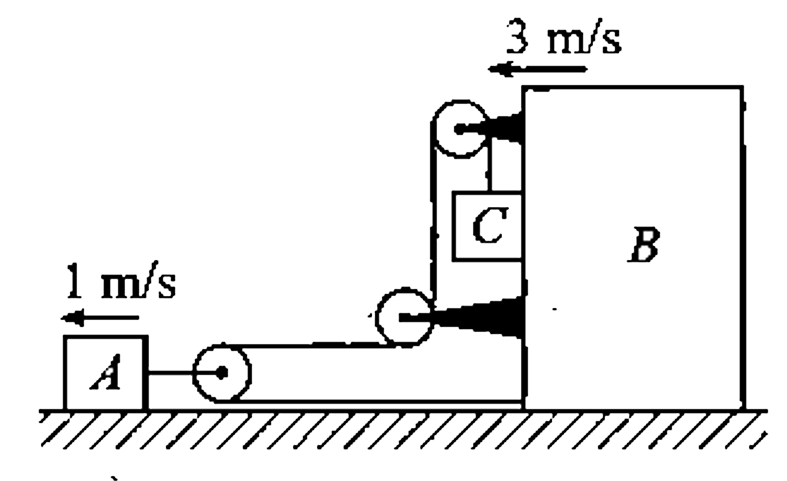 A5 m/sB2 m/sC3 m/sD4 m/s
A5 m/sB2 m/sC3 m/sD4 m/sFind out velocity of block B in the given figure : (all the pulleys are ideal and string are inextensible massless)
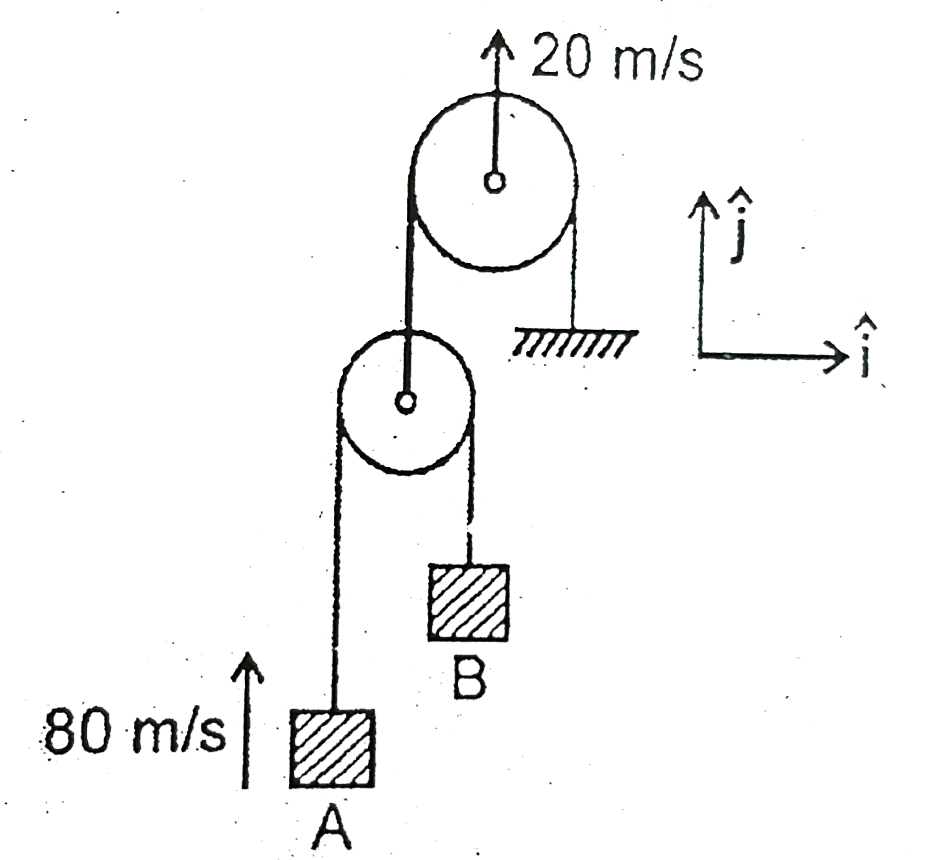 A80m/sˆjB−40m/sˆjC0m/sˆjD−80m/sˆj
A80m/sˆjB−40m/sˆjC0m/sˆjD−80m/sˆjThere blocks a,b and c of massses 10 kg ,10 kg and 20 kg respectivaly are arrenged as shown in figure all the surface are frictionless and string is inextensible A constant force F= 20N MN is applied on block a as shown .pulley and string are light . part of block a as shown . pulley and string are light . part of the string connecting both pulleys is vertical and part of hte stings connecting pulleys with masses a and b are horizontal .
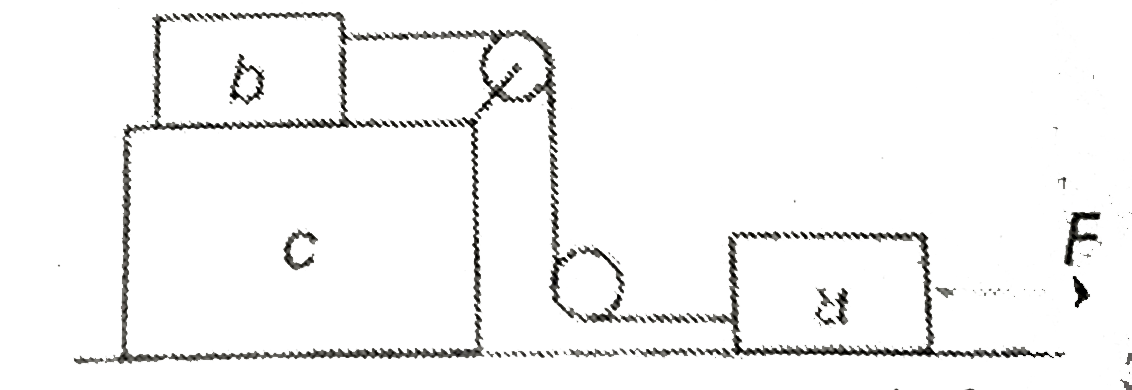 AAcceleration of block b 0.5m/s2BAcceleration of block b is 1m/s2CTension in the string is 10NDAcceleration of block c is 0.5m/s2
AAcceleration of block b 0.5m/s2BAcceleration of block b is 1m/s2CTension in the string is 10NDAcceleration of block c is 0.5m/s2
A pulley-rope-mass arrangement is shown in fig. Find the acceleration of block m1 when the masses are set free to move. Assume that the pulley and the ropes are ideal.
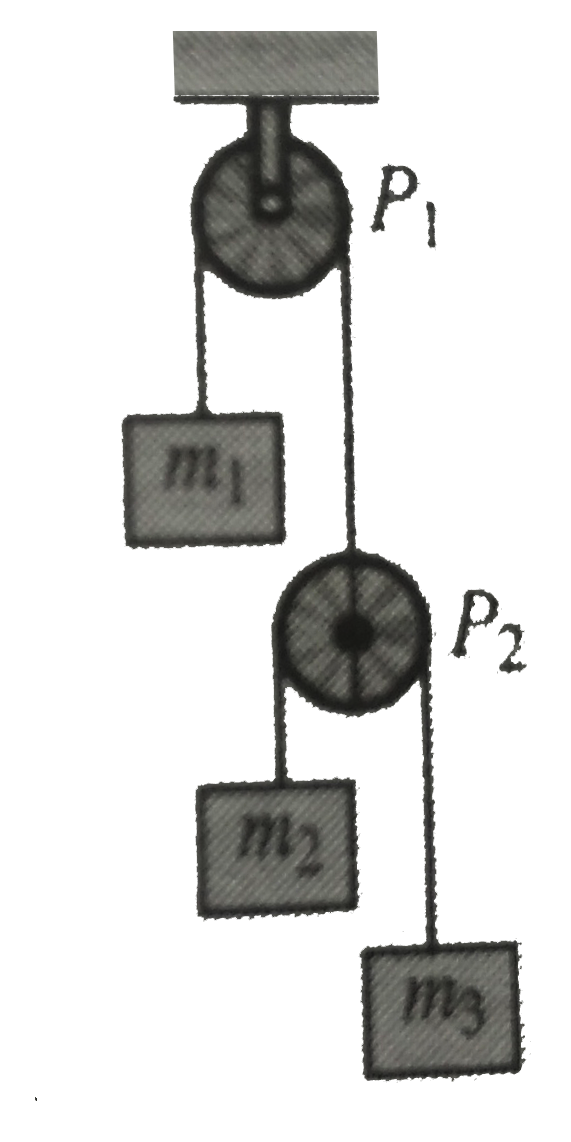
View SolutionFind the acceleration blocks in fig. The pulley and the string are massless.

View SolutionIf block B shown in figure-l.78(a) is going down with acceleration 5m/s2, find the acceleration of the block A. All pulleys and strings are ideal. Radii ratio for the two step pulleys are 1:3:5 and 1:2.
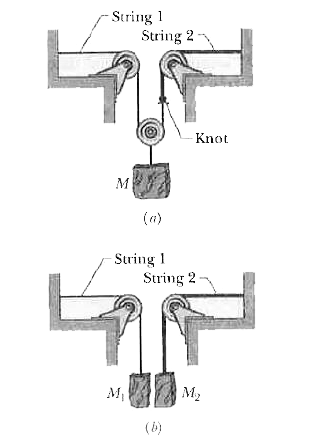
View SolutionIn fig. 16-47a, string 1 has a linear density of 3.00 g/m, and string 2 has a linear density of 5.00 g/m. They are under tension due to the hanging block of mass M= 800 g. Calculate the wave speed on (a) string 1 and (b) string 2 (Hint: When a string loops halfway around a pulley, it pulls on the pulley witii a net force that is twice the tension in the string) Next the block is divided into two blocks (with M1+M2=M) and the apparatus in tearranged as shown in fig. 16-47b. Find (c) M1and(d)M2 such that the wave speeds in the two strings are equal.
View SolutionIn Fig. find the acceleration a of the system and the tesnions T1 and T2 in the strings. Assume that the table and the pulleys are frictionless and the strings are massless. Take g = 9.8ms2

View Solution