
Two blocks are connected by an inextensible string as shown. The pulley is fixed. If block A moves down with speed v, find the velocit of block B at instant.
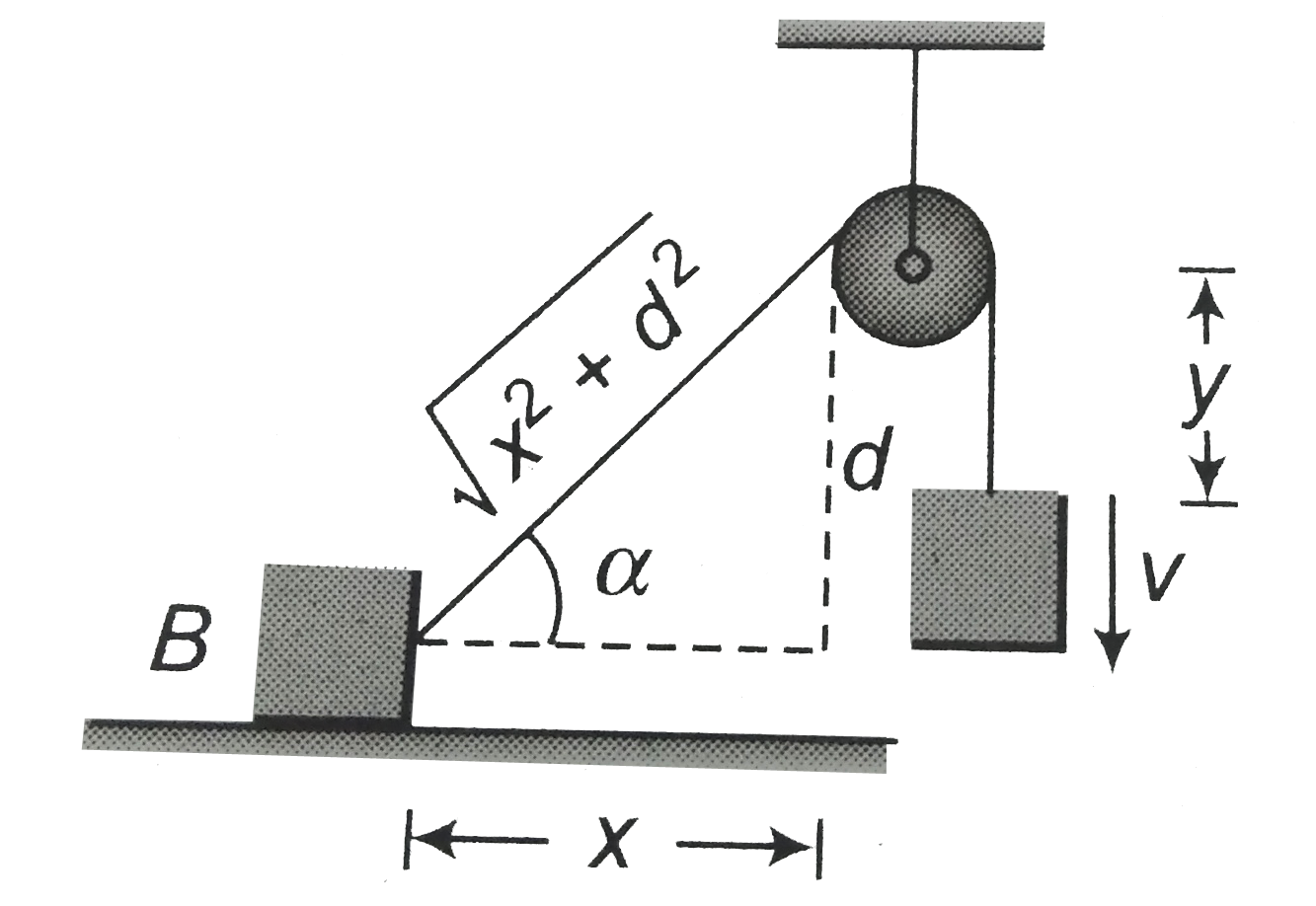
Length of the string is constant
L=√x2+d2+y=(x2+d2)1/2+y
Differentiating w.r.t. time t, we get
dLdt=12(x2+d2)−1/2(2xdxdt+0)+dydt
dLdt=0 [as L and d are constant]
dxdt=−vB [ x is decreasing with time]
dydt=v
0=−xvB√x2+d2+v=−vBcosα+v
vB=vcosα
vB: horizontal velocity of B
vB=cosα=v
vB=vcosα
Topper's Solved these Questions
Similar Questions

The smooth ring A can slide on a fixed horizontal rod as shown the pulley is fixed. If some instant velocity of ring is v, find the velocity of block at that instant.
View SolutionTwo blocks are connected by an inextensible light string, the string is passing over smooth, light pulley as shown. Find the acceleration of blocks and tension in the string, reaction in pulley.

View Solution
Knowledge Check
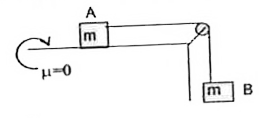
A system of two blocks A and B are connected by an inextensible massless string as shown in Fig. The pulley is massless and frictionless. Initially, the system is at rest. A bullet of mass m moving with a velocity u as shown hits block If and gets embedded into it. The impulse imparted by tension force to the block of mass 3m is
 A5mu4B4mu5C2mu5D3mu5
A5mu4B4mu5C2mu5D3mu5Figure shows two blocks connected by a light inextensible string as shown in figure. A force of 10 N is applied on the bigger block at 60∘ with horizontal, then the tension in the st ring connection the two masses is -
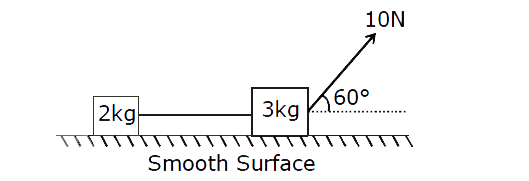 A5 NB2 NC1 ND3 N
A5 NB2 NC1 ND3 NIf block A is moving horizontally with velocity vA, then find the velocity of block B at the instant as shown in fig.
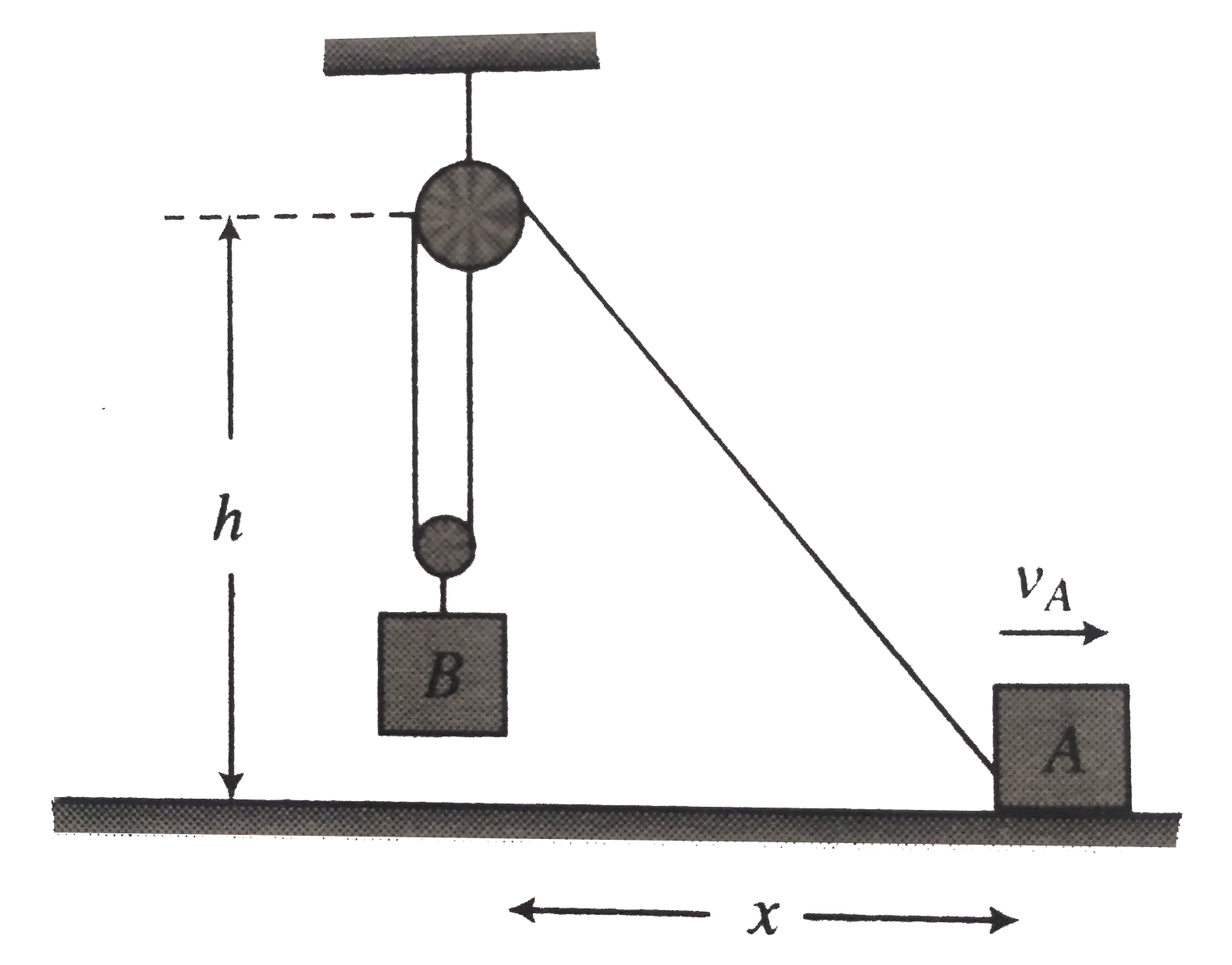 AhvA2√x2+h2BxvA√x2+h2CxvA2√x2+h2DhvA√x2+h2
AhvA2√x2+h2BxvA√x2+h2CxvA2√x2+h2DhvA√x2+h2
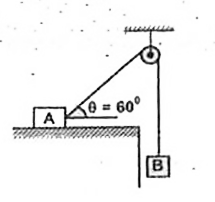
Two blocks A & B are connected by a light inextensible string passing over a fixed smooth pulley as shown in the figure. The coefficient of friction between the block A and the horizontal table is μ=0.2. If the block A is just to slip, find the ratio of the masses of the blocks.
View SolutionA bead C can move freely on a horizontal rod. The bead is connected by blocks B and D by a string as shown in the figure. IF the velocity of B is v. find the velocity of block D.
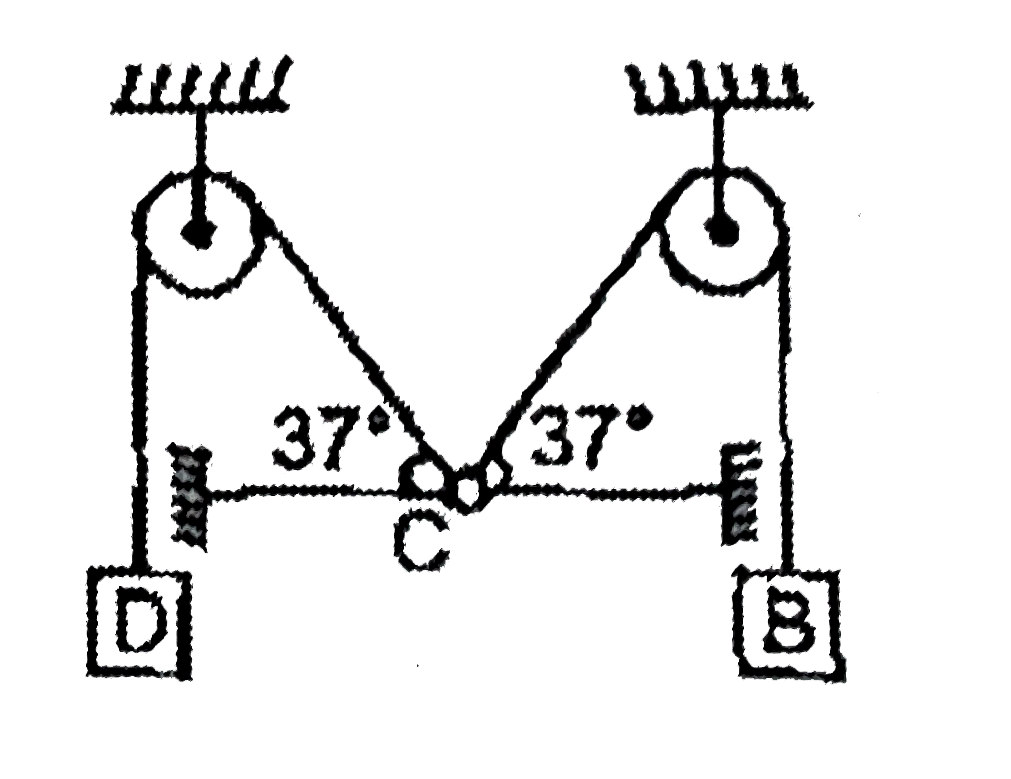
View Solution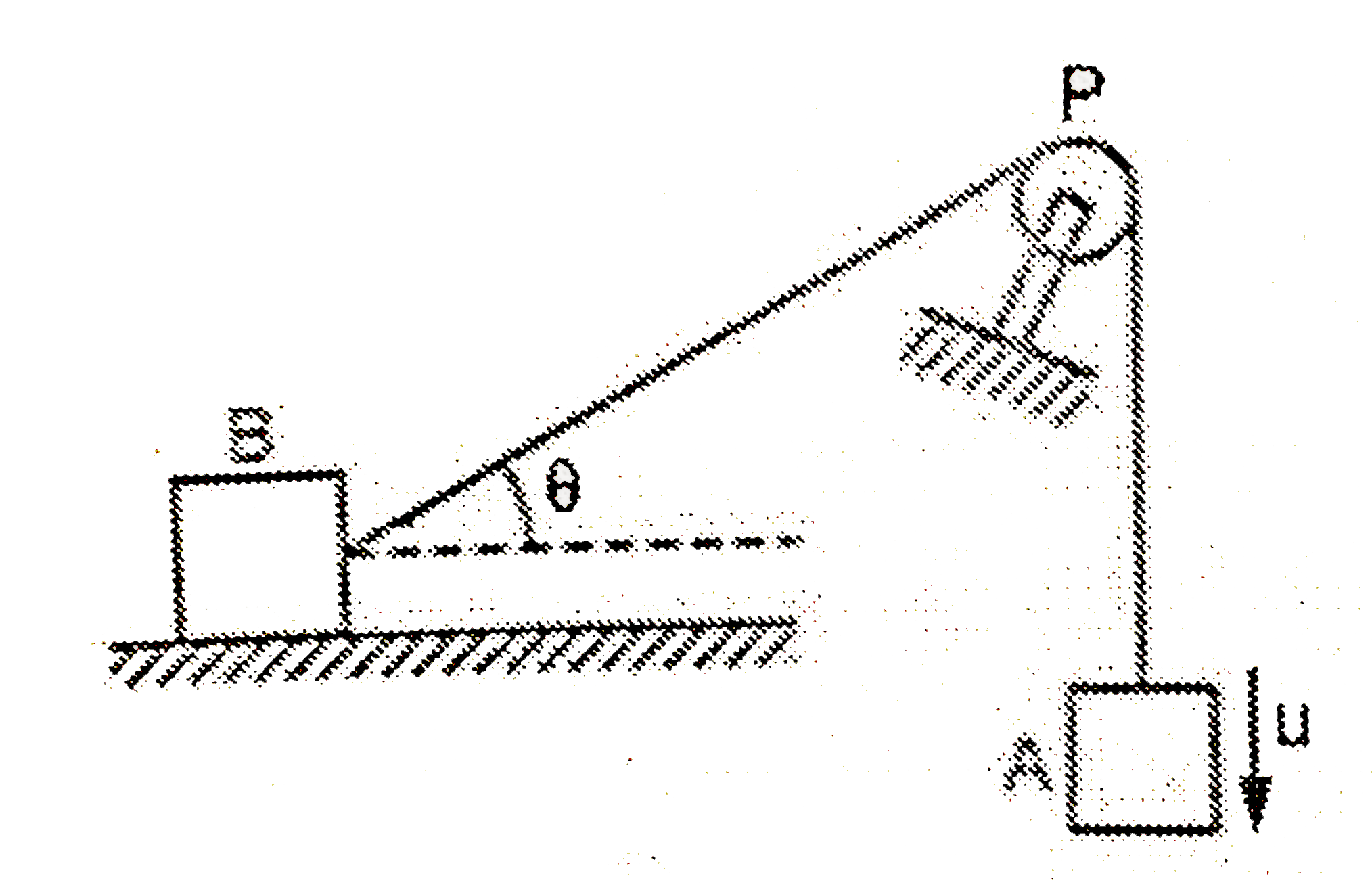
In the figure, the blocks are of equal mass. The pulley is fixed. In the position shown, A moves down with a speed u, and vB= the speed of B.
View SolutionTwo blocks A & B are connected by the massless string & pulley. As the blocks are left to move, the force by the pulley on the clamp is
View SolutionTwo blocks A and B are connected by a light inextensible string passing over a fixed smooth pulley as shown in figure The coefficient of friction between the block A and B the horizontal table is μ=0.5. If the block A is just , find ratio of the masses of the blocks
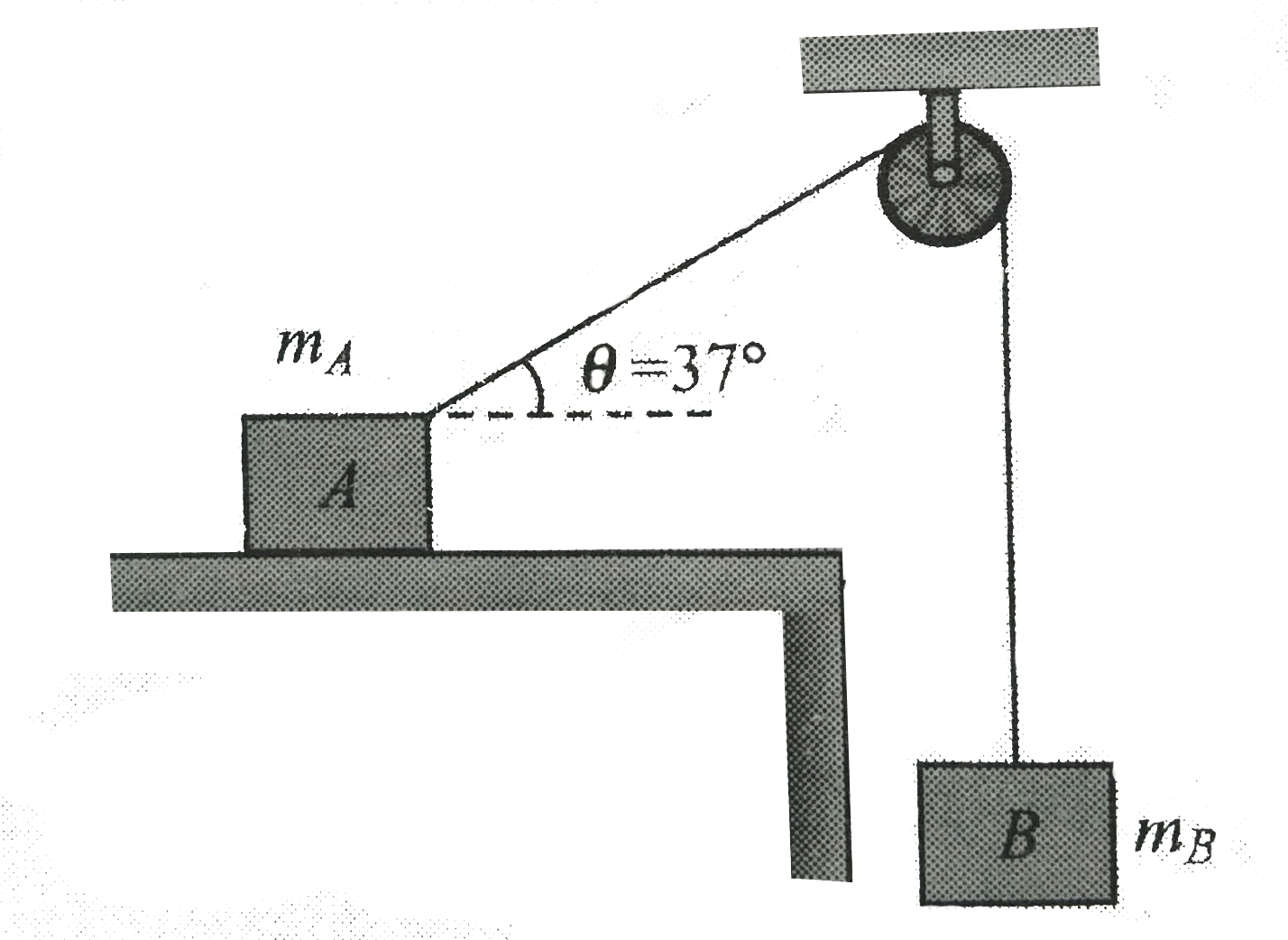
View Solution
