A butterfly is flying with velocity 10ˆi+12ˆjm/s and wind is blowing along x axis with velocity u . If butterfly starts motion from A and after some time reaches point B, find the value of u.
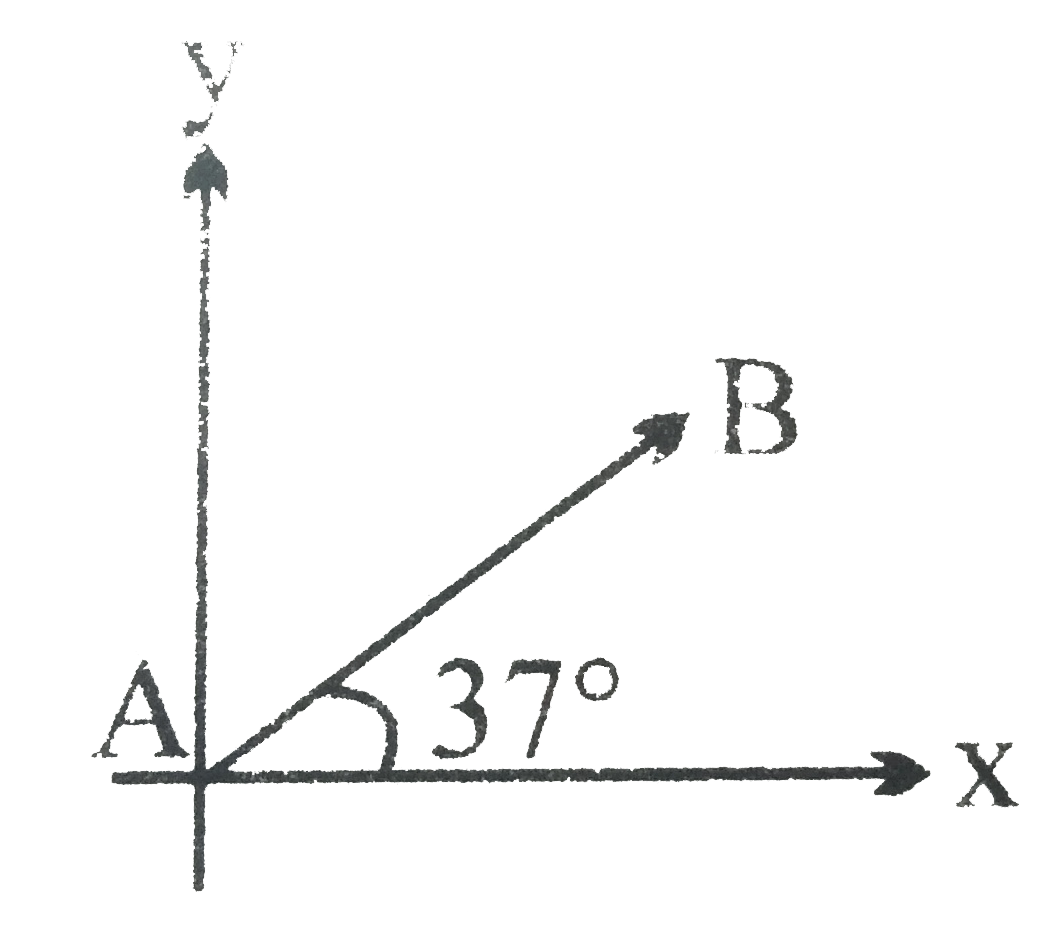
The correct Answer is:6m/s
→VR=(10+u)ˆi+12ˆj
tan37∘=1210+u
34=1210+u
30+3u=48⇒3u=18⇒u=6m/s
Similar Questions
A butterfly is flying with a velocity 4√2m/s in North-East direction. Wind is slowly blowing at 1 m/s from North to South. The resultant displacement of the butterfly in 3 seconds is :
View SolutionThree particles start from the origin at the same time, one with velocity u1 along the x-axis, the second with velocity u2 along the y-axis . Find the velocity of the third particles, along the x=y line so that the three particles may always lie on the same straight line.
View Solution
Knowledge Check
A body is projected vertically upwards with some velocity u. It is at the same point at t=6s as was at t=4s. Find the value of u.
A30m/sB40m/sC20m/sD50m/sVelocity time graphs of particles A and B moving along x-axis are shown here. Both A and B start from origin:
 AMaximum separation between the particles is 8mBMaximum separation between the particles is 10mCMaximum separation between the particles occurs at t=6sDMaximum separation between the particles occurs at t=8s
AMaximum separation between the particles is 8mBMaximum separation between the particles is 10mCMaximum separation between the particles occurs at t=6sDMaximum separation between the particles occurs at t=8sA body projected vertically upwards with a velocity u returns to the starting point in 4 seconds. If g=10m/sec, the value of u is
A5m/secB10m/secC15m/secD20m/sec
An object is projected with velocity →v0=15ˆj+20ˆj . Considering x along horizontal axis and y along vertical axis. Find its velocity after 2s.
View Solution(a) A particle moving with constant acceleration from A to B in a straight line AB has velocities u and v at A and B respectively. Find the velocity of the particle at the midpoint of AB.
(b) If the time taken by the particle to go from A to the midpoint of AB is two times that from the midpoint of AB to B then find the value of v/u.
View SolutionA projectile is given an initial velocity of (ˆi+2ˆj)ms, where ˆi is along the ground and ˆj is along the vertical. If g=10ms−2, the equation of its trajectory is
View SolutionA particle at origin (0,0) moving with initial velocity u=5msˆj and acceleration 10ˆi+4ˆj. After t time it reaches at position (20,y) then find t & y
View SolutionAt the start of a motion along a line the initial velocity is u and acceleration is at. The final velocity v after time t, is
View Solution

