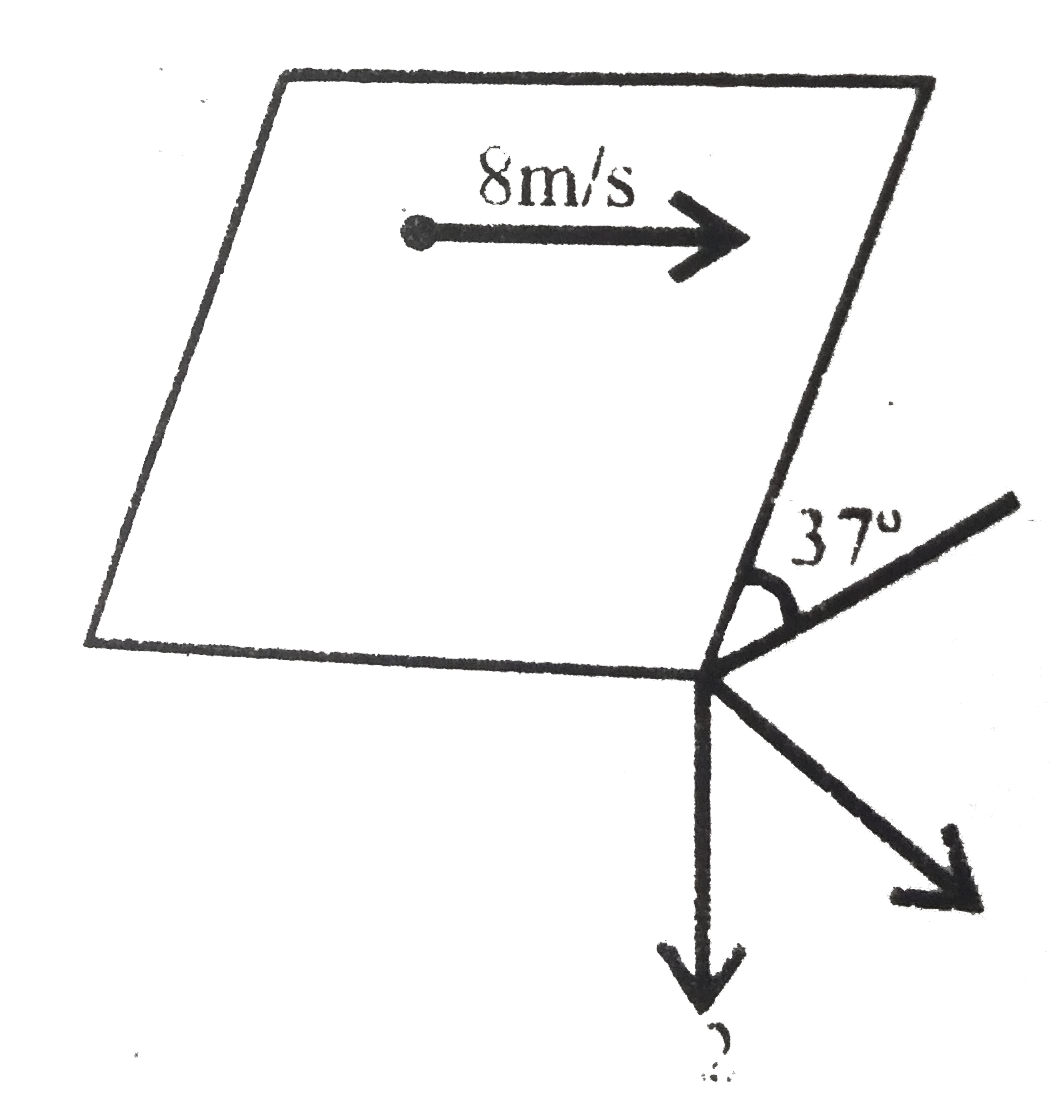
A ball is projected on smooth inclined plane in direction perpendicular to line of greatest slope with velcoity of 8m/s. Find it's speed after 1sec.

The correct Answer is:10m/s
component of g⊥ to velcoity is gsin37∘
vx=8m/s
vy=gsin37∘t
⇒vy=10×0.6×1
⇒vy=6m/s
v=√v2x+v2y
⇒v=√(8)2+(6)2⇒v=10ms
Similar Questions
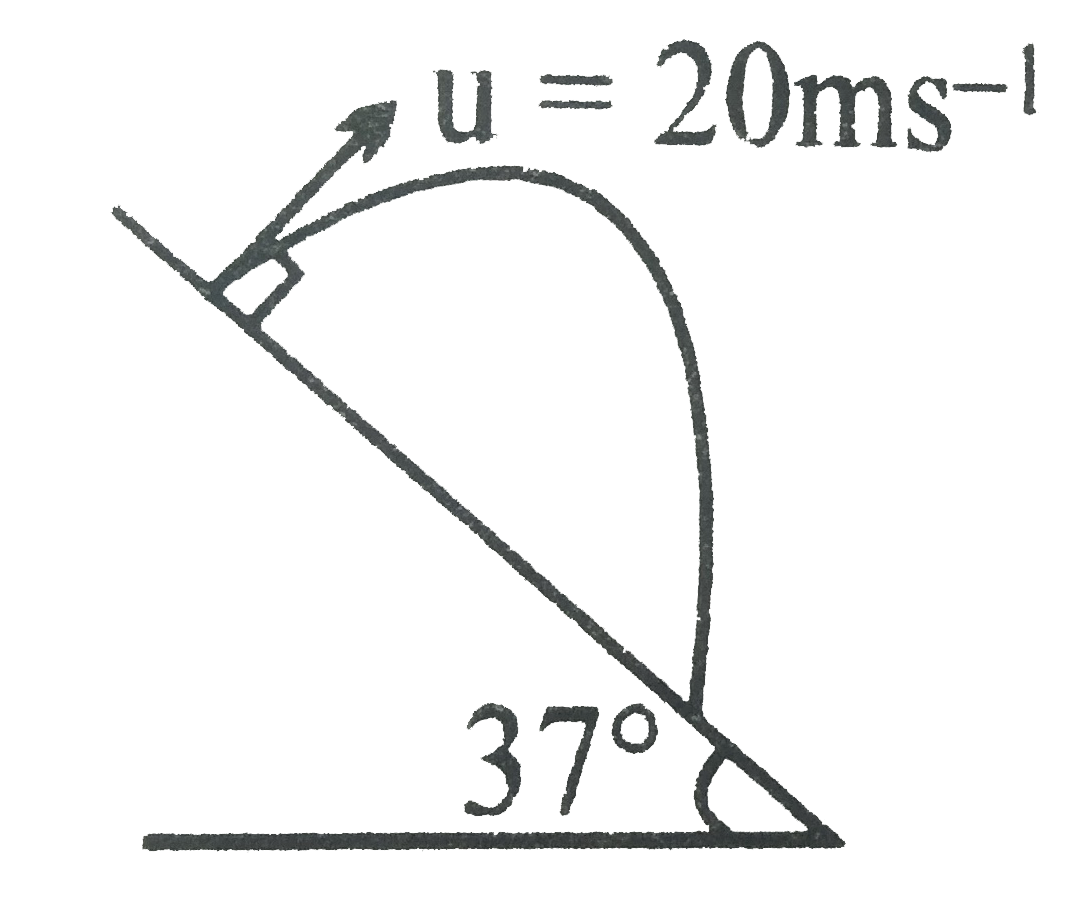
Find range of projectile on the inclined plane which is projected perpendicular to the incline plane with velcoity 20m/s as shwon in figure.
View SolutionA small ball is projected up a smooth inclined plane with an initial speed of 10m/s at 30∘ from the bottom edge of the slope. It returns to the edge after 2s. The ball is in contact with the inclined plane throughout the process. The inclination angle (in degree) of the plane is N. The value of N/6 is
View Solution
Knowledge Check
A particle is projected up a smooth inclined plane of inclination 60∘ along the line of greatest slope. If it comes to instantaneous rest after 2 seconds, then the velocity of projection is (g=9.8m/sec2)
A9.8m/sB10m/sC16.97m/sD19.6m/sA small ball is projected up a smooth inclined plane with an initial speed of 10m/s along the direction at 30∘ to the bottom edge of the slope. It returns to the edge after 2s. The ball is in constant with the inclined plane throughout the process. What is the inclination angle of the plane?
 A15∘B60∘C37∘D30∘
A15∘B60∘C37∘D30∘A small ball is projected up a smooth inclined plane with an initial speed of 10m/s along the direction at 30∘to the bottom edge of the slope .It returns to the edge after 2s . The ball is in contact with the inclied plane throughout the process. The angle of inclination θ is :−.
 A45∘B53∘C30∘D37∘
A45∘B53∘C30∘D37∘
A uniform solid cylinder of mass M and radius R rolls a rough inclined plane with its axis perpendicular to the line of greatest slope as shown in figure-5.75. As the cylinder rolls it winds up a light string which passes over a light and smooth pulley and attached to a mass m , the part of the string between pulley and cylinder being parallel to the line of greatest slope. Prove that the tension in the string is
T=[(3+4sinθ)Mmg3M+8m]

View SolutionFrom a point on the side of a hill two bodies are projected in the vertical plane through the line of greatest slope with same velocity, but in directions at right angles to each other. The difference of their ranges is independent of the angles of projection.
View SolutionA ball is projected form a point A on a smooth inclined plane which makes an angle a to the horizontal. The velocity of projection makes an angle θ with the plane upwards. If on the second bounce the ball is moving perpendicular to the plane, find e in terms of α and θ. Here e is the coefficient of restitution between the ball and the plane.
View SolutionA wedge of mass M and angle α rests on a smooth horizontal plane. A smooth sphere of mass m strickes it in a direction perpendicular to its inclined face and rebounds. If the coefficient of restitution is e, find the ratio of the speed of the sphere just before and just after the impact.
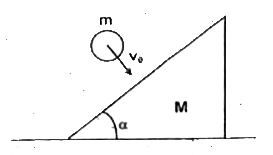
View Solution
A particle is projected from surface of the inclined plane with speed u and at an angle θ with the horizontal. After some time the particle collides elastically with the smooth fixed inclined plane for the first time and subsequently moves in vertical direction. Starting from projection, find the time taken by the particle to reach maximum height. (Neglect time of collision).
View Solution