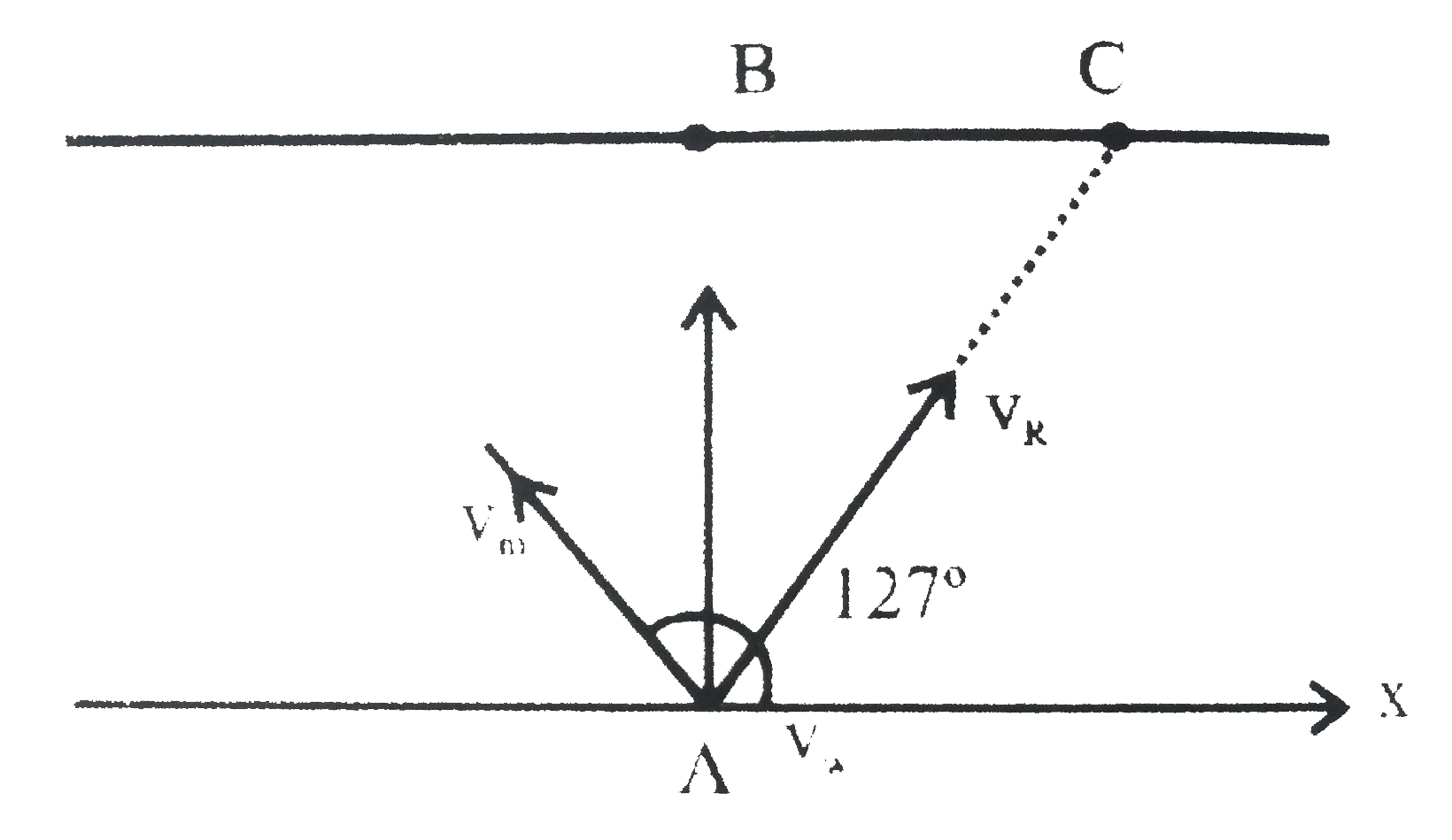
A swimmer swims in still water at a speed =5km/hr. He enters a 200m wide river, having river flow speed =4km/hr at point A and proceeds to swim at an angle of 127∘(sin37∘=0.6) with the river flow direction. Another point B is located directly across A on the other side. the swimmer lands on the other bank at a point C, form which he walks the distance CB with a speed =3km/hr. The total time in which he reaches from A to B is
5minutes
4minutes
3minutes
None
The correct Answer is:B
VRY=Vmy+Vwy
=5sin127∘
=5cos37∘
=9×0.8
4km/H
=4×510m/s
time taken to cross river tAB=200×184×5sec
t=180sec=3min
VR(X)=Vmx+Vmx⇒VR(X)=5cos127∘+4
VR(X)=5(−sin37∘)+4⇒VR(X)=−3+4
⇒VR(X)=1km/h=518m/s
Horizontal drag BC
=VRx×t=518ms×180sec=50m
Time taken to reach form B to C
tBC=distancespeed⇒tBC=503×518m/s
=60sec=1min
total time =4min.
Similar Questions
A swimmer can swim in still water with a speed of 2.5 m/s. What is the shortest time taken by him to swim across the river?
View SolutionA man can swim at a speed of 5km/h in the still water. He wants to cross a 1600m wide river flowing at 4km/h. He keeps himself at an angle 127∘ with the river flow while swimming. (a) Find the time he takes to cross the river. (b) Find the distance traveled by him along the flow.
View Solution
Knowledge Check
A person can swim in still water with speed =5km/hr. He enters a 200m. Wide river at a point A on one of the banks. The river flow velocity is uniform and equal to 6km/hr. A point B is located directly across. A, on the other bank. What is the closest possible distance from B where the swimmer can land on the other bank ?
A120mB40√11mC30√10mDNone of theseA man can swim at a speed of 3kmh−1 in still water. He wants to cross a 500−m wide river flowing at 2kmh−1. He keeps himself always at an angle to 120∘ with the river flow while swimming.
The time taken to cross the river is.A32hB16hC13√3hDnoneA swimmer crosses a river of width d flowing at velocity v. While swimming, he keeps himself always at an angle of 120∘ with the river flow and on reaching the other end. He finds a drift of d/2 in the direction of flow of river. The speed of the swimmer with respect to the river is :
A(2−√3)vB2(2−√3)vC4(2−√3)vD(2+√3)v
A man can swim at a speed of 3 km/h in still water. He wants t cross a 500 m wide river flowing at 2 km/h. He flow at an angle of 120 with the river flow while swimming. A. Find the time he takes to cross the river. b.At what point on the opposite bank will he arrive?
View SolutionA person is swimming with a speed of 10 m/s at an angle of 120° with the flow and reaches to a point directly opposite on the other side of the river. The speed of the flow is 'x m/s.
The value of 'x to the nearest integer is_________.
View SolutionA man can swim in still water ast a speed of 3 km/h. He wants to cross a river that flows at 2 km/h and reach the point directly oposite to his starting point. A. In which diretionshoeld he try to swim (that is, find the angle his body makes wilth the river flow)? b. How much time will he take to cross the river if the river is 500 m wide?
View SolutionA boat man can rown with a speed of 10kmh−1 in still water. If the river flows steadily at 5km/h, in which direction showld the boatman row in order to reach a point on the other bank directly opposite to the point from wher he stared ? The width of the river is 2km.
View SolutionA man can swim at a speed of 5 km/h W.r.t water. He wants to cross a 1.5 km wide river flowing at 3 km/h. He keeps himself always at an angle of 60° with the flow of direction while swimming, The time taken by him to cross the river will be
View Solution
