A particle is projected form a horizontal plane (x−z plane) such that its velocity vector at time t is gives by →V=aˆi+(b−ct)ˆj. Its range on the horizontal plane is given by
bac
2bac
3bac
None
The correct Answer is:B
To find the range of the particle projected from the horizontal plane (the x-z plane) with the given velocity vector →V=a^i+(b−ct)^j, we can follow these steps:
Step 1: Identify the components of the velocity vector
The velocity vector is given as:
→V=a^i+(b−ct)^j
From this, we can identify the horizontal and vertical components of the velocity:
- Horizontal component (Vx): a
- Vertical component (Vy): b−ct
Step 2: Determine the time of flight
The vertical motion is affected by the downward acceleration due to gravity. In this case, the downward acceleration is represented by −c. The vertical velocity can be expressed as:
Vy=b−ct
To find the time of flight, we need to determine when the particle returns to the horizontal plane (i.e., when y=0). The vertical position y can be found by integrating the vertical velocity:
y(t)=∫(b−ct)dt=bt−12ct2+y0
Assuming the particle starts from the horizontal plane (y0=0), we set y(t)=0 to find the time of flight:
0=bt−12ct2
Factoring out t:
t(bt−12ct)=0
This gives us two solutions:
1. t=0 (initial time)
2. bt−12ct=0⇒t=2bc
Step 3: Calculate the horizontal range
The horizontal range R can be calculated using the horizontal component of the velocity and the total time of flight:
R=Vx⋅ttotal
Substituting the values:
R=a⋅2bc
Thus, the range R is given by:
R=2abc
Final Answer
The range on the horizontal plane is:
R=2abc
---
The velocity vector is given as:
→V=a^i+(b−ct)^j
From this, we can identify the horizontal and vertical components of the velocity:
- Horizontal component (Vx): a
- Vertical component (Vy): b−ct
The vertical motion is affected by the downward acceleration due to gravity. In this case, the downward acceleration is represented by −c. The vertical velocity can be expressed as:
Vy=b−ct
To find the time of flight, we need to determine when the particle returns to the horizontal plane (i.e., when y=0). The vertical position y can be found by integrating the vertical velocity:
y(t)=∫(b−ct)dt=bt−12ct2+y0
Assuming the particle starts from the horizontal plane (y0=0), we set y(t)=0 to find the time of flight:
0=bt−12ct2
Factoring out t:
t(bt−12ct)=0
This gives us two solutions:
1. t=0 (initial time)
2. bt−12ct=0⇒t=2bc
The horizontal range R can be calculated using the horizontal component of the velocity and the total time of flight:
R=Vx⋅ttotal
Substituting the values:
R=a⋅2bc
Thus, the range R is given by:
R=2abc
The range on the horizontal plane is:
R=2abc
Similar Questions
A particle is projected from origin in xy-plane and its equation ,of trajectory is given by y=ax−bx2. The only acceleration ,in the motion is' f' which is constant and in −ve direction of, y-axis.
(a) Find the velocity of projection and the angle of projection.
(b) Point of projection is considered as origin and x-axis along the horizontal ground. Find the horizontal range: and maximum height of projectile. Projectile completes its flight in horizonal plane of projection.
View SolutionA particle is projected up an inclines plane. Plane is inclined at an angle θ with horizontal and particle is projected at an angle α with horizontal. If particle strikes the plane horizontally prove that tanα=2tanθ
View Solution
Knowledge Check
The velocity at the maximum height of a projectile is half of its velocity of projection u. Its range on the horizontal plane is
A3u2gB√3u22gC3u2g2Du23g
A particle is projected from the horizontal x-z plane, in vertical x-y plane where x-axis is horizontal and positive y-axis vertically upwards. The graph of y coordinate of the particle v/s time is as shown . The range of the particle is √3. Then the speed of the projected particle is:A√3msB√4034msC2√5msD√28msA particle is projected from a horizontal plane with a velocity of 8√2ms−1 ms at an angle θ. At highest point its velocity is found to be 8ms−1 Its range will be (g=10ms−2)
A3.2 mB4.6 mC6.4 mD12.8 m
A particle is projected with initial velocity u making an angle α with the horizontal, its time of flight will be given by
View SolutionA particle is projected with a velocity v such that its range on the horizontal plane is twice the greatest height attained by it. The range of the projectile is (where g is acceleration due to gravity)
View SolutionA ball is projected horizontally from an inclined plane with a velocity V, as shown in the figure. It will strike the plane after a time

View SolutionA particle projected from origin moves in x-y plane with a velocity →v=3ˆi+6xˆj, where ˆi and ˆj are the unit vectors along x and y axis. Find the equation of path followed by the particle :-
View SolutionA particle is to be projected horizontally with velocity v from a point P, which is 60m above the foot of a plane inclined at angle 45∘ with horizontal as shown in figure. The particle hits the plane perpendicularly at A. After rebound from inlined plane it again hits at B. If coefficient of restitution between particles and plane is 1√2 then,
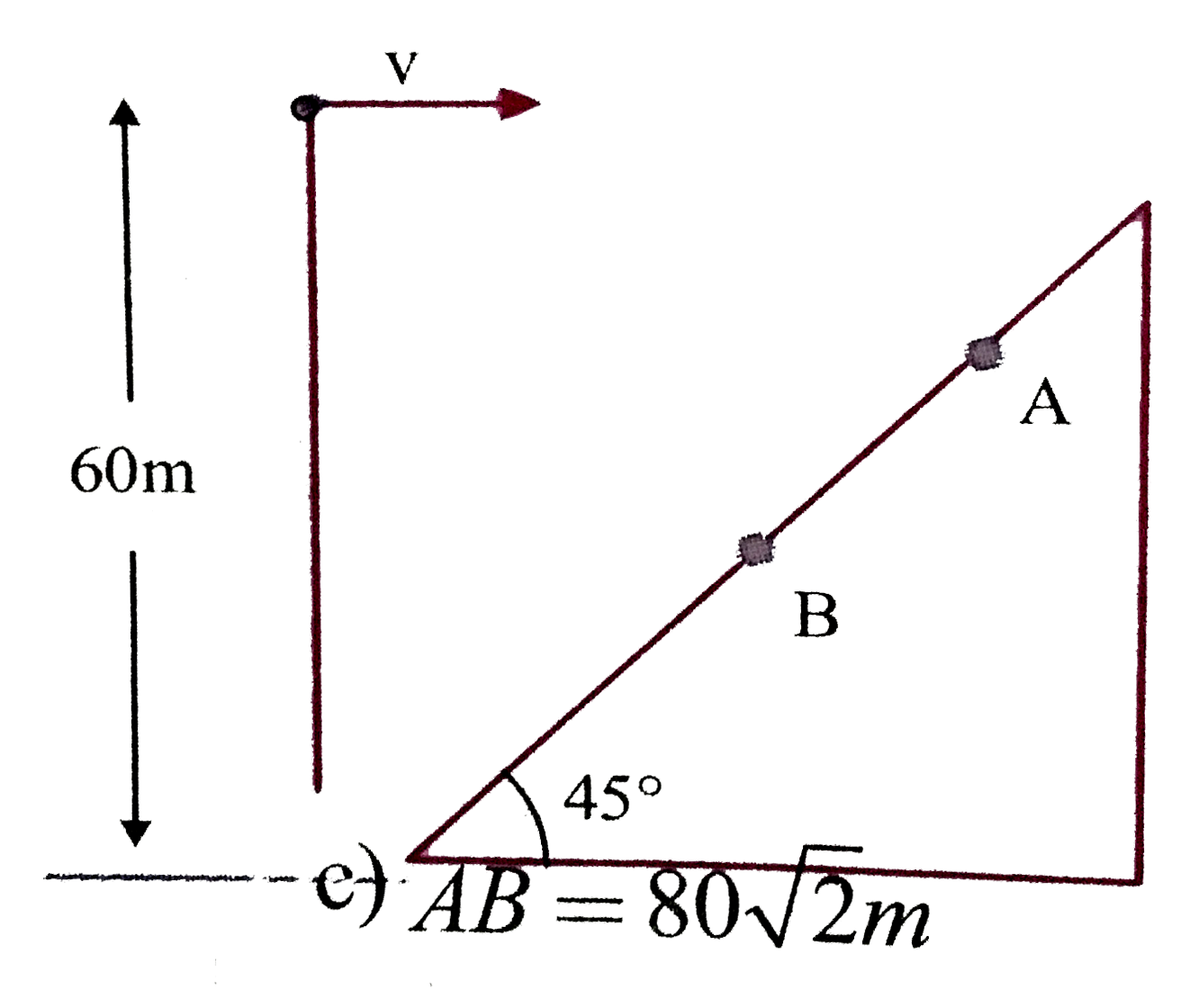
View Solution
