Calculate the capacitance of a parallel plate capacitor, with plate area A and distance between the plates d, when filled with a dielectric whose permittivity varies as
∈(x)=∈0+kx(0<x<d2),∈(x)=∈0+k(d−x)(d2<x≤d).
The correct Answer is:A, B, D
1C1=∫1dC1=d/2∫0dx(∈0+βx)A
=1βA[ln(∈0+βx)]d/20
1C1=1βA[ln(∈0+βd2)−ln∈0]
=1βAln(2∈0+βd2∈0)
1C2=∫1dC2=1Ad∫d/2dx∈0+β(d−x)
=−1βA[ln{∈0+β(d−x)}]dd/2
1C1=1βA[ln{∈0+β(d−d)}]−ln[∈0+βd2]
=−1βA[ln∈0−ln2∈0+βd2]
1C2=−1βAln(2∈0)2∈0+βd
1C2=1βAln2∈0+βd2∈0
1C=1C1+1C2=1βA[2ln2∈0+βd2∈0]
C=βA/2ln2∈0+βd2∈0
Similar Questions
Calculate the capacitance of a parallel plate condenser, with plate area A and distance between plates d, when filled with a dielectric whose dielectric constant varies as,
K(x)=1+βx∈0 0<x<d2, K(x)=1+β∈0(d−x) d2<x<d.
For what value of β would the capacity of the condenser be twice that when it is without any dielectric?
View SolutionThe plates of a parallel plate capacitance 1.0 F are separated by a distance d =1 cm. Find the plate area .
View Solution
Knowledge Check
The capacitance of the capacitors of plate areas A1 and A2(A1<A2) at a distance d is
 Aε0A1dBε0A2dCε0(A1+A2)2dDε0√A1A2d
Aε0A1dBε0A2dCε0(A1+A2)2dDε0√A1A2dThe force between the plates of a parallel plate capacitor of capacitance C and distance of separation of the plates d with a potential difference V between the plates, is.
ACV22dBC2V22d2CC2V2d2DV2dC
A parallel plate capacitor with plate area 'A' and distance of separation 'd' is filled with a dielectric. What is the capacity of the capacitor when permittivity of the dielectric varies as : ε(x)=ε0+kx, for (0<x≤d2)
ε(x)=e0+k(d−x), for (d2≤x≤d)
View SolutionThe distance between the plates fo a parallel plate capacitor is d. A metal plate of thickness d/2 is placed between the plates, what will be the new capacity ?
View SolutionIn a parallel plate capacitor distance between the plate is 'd'. If dielectric of variable permeability is filled as
ε(x)=ε0+kx,0<x≤d2
ε(x)=ε0+k(d−x),d2<x≤d
Find capacitance.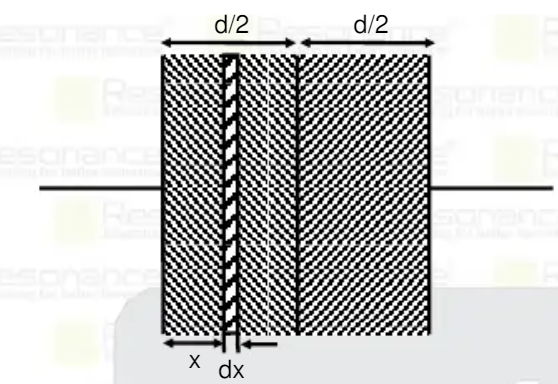
View SolutionThe capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.

View SolutionThe capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.

View SolutionThe' distance between the plates of a parallel plate capacitor is d. A metal plate of thickness d/2 is placed between the plates. What will e its effect on the capacitance.
View Solution