Three charges Q, +q and +q are placed at the vertices of a right-angled isosceles triangle as shown. The net electrostatic energy of the configuration is zero if Q is equal to
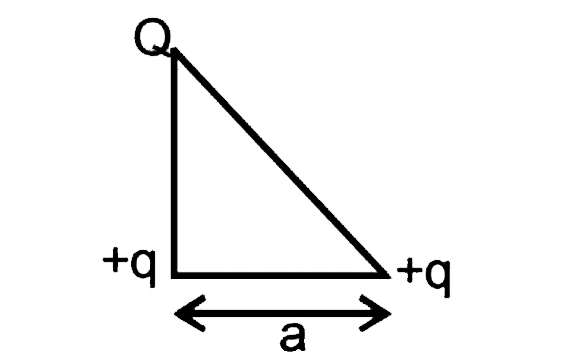
−q1+√2
−2q2+√2
−2q
+q
(b) The net eelctrostatic enrgy is
U=KQqa=KQq√2a+Kqqa=0
Q+Q√2+q=0
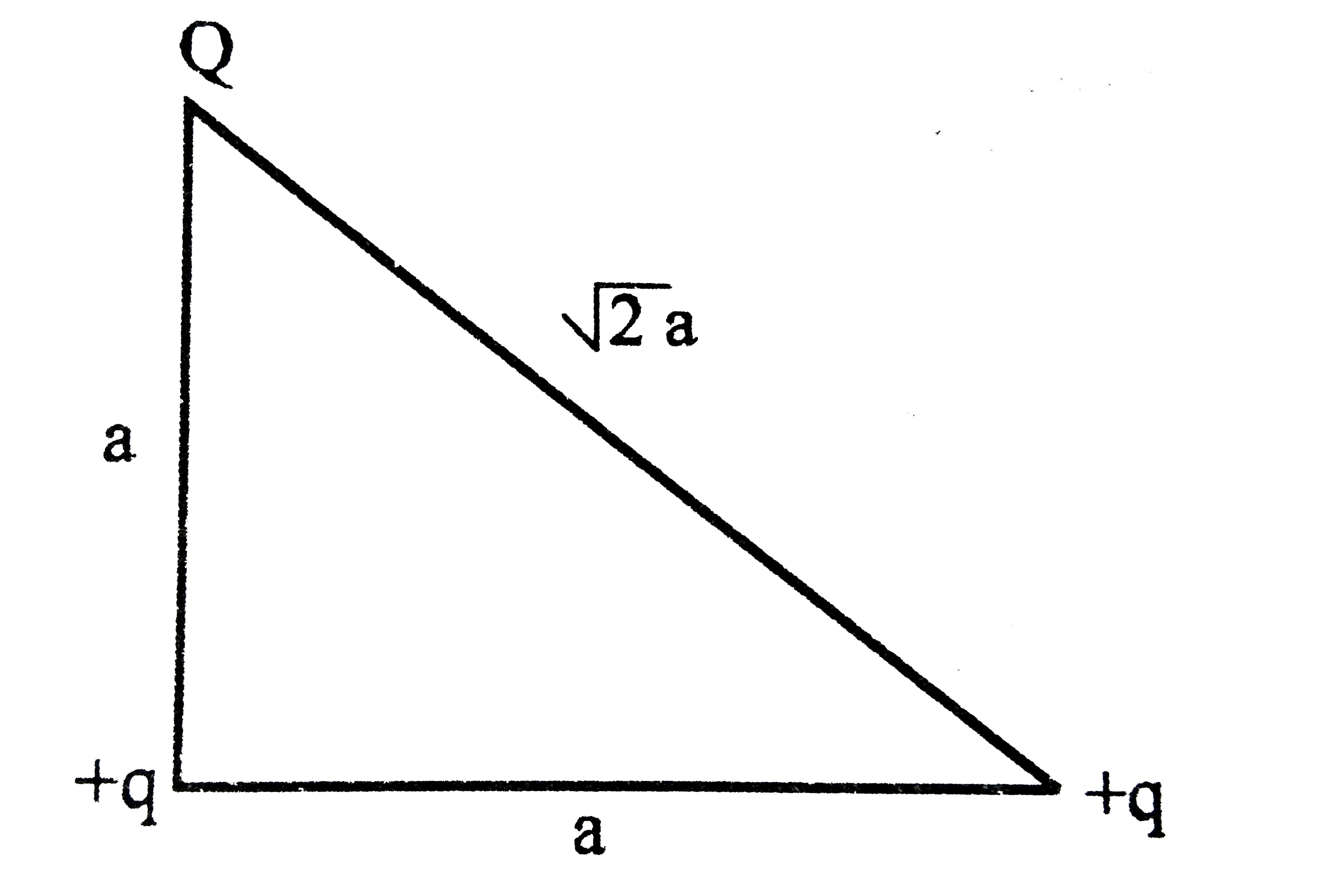
which gives Q=−q(√2√2+1=−2q2+√2
(c ) 
E1 is field due to 8μC and 8μC at P will be in the direction of OP while →E2 due to −1μC and −1μC will be in the direcition of PO For Ep=0 at P(OP=x)
2E1csα=2E2cosθ
2K×8×10−6(√273/22+x2)×x((√3/2)2+x2)1/2
x=−+√52
For OP>x,Ep will be towards OP and for OP<x,Ep will be tward OP for Ep=O From cosnervation of energy
(i) For least value of V to cross origing
Loss of K.e.=Gain of P.E.
12mv20=qVp ....(1)
v+p = 2 xx 9 xx10^9 [(8 xx 10^(-4))/(sqrt ((sqrt (27)/2)^2 + (sqrt 5/2)^2) sqrt) - (1 xx 1-^(-6))/(sqrt ((sqrt 3/2)^2) +( sqt 5/2))^2]
Vp=27000 volt ...(2)
Form (1) and (2)
12×6×10−4×v20=0.−6×2700
v20=9
v0=3m/s
(ii) For KE at origin
Potential at origin v0=10−7×2×9×109
[8×10−6√27/2−1×10−6√3/2]=2.4×104 volt
KE at origin=q(V0−Vp)=−0.1×10−6
(24000−27000)=3×10−4J.
Similar Questions
Three charges Q, +q and +q are placed at the vertices of a right-angle isosceles triangle as shown in Fig. The net electrostatic energy of the configuration is zero if Q is equal to :-

View SolutionThree charges Q+q and + q are placed at the vertices of a right -angle isosceles triangle as shown below. The net eletrostatic energy of the configuration is zero if the value of Q is :
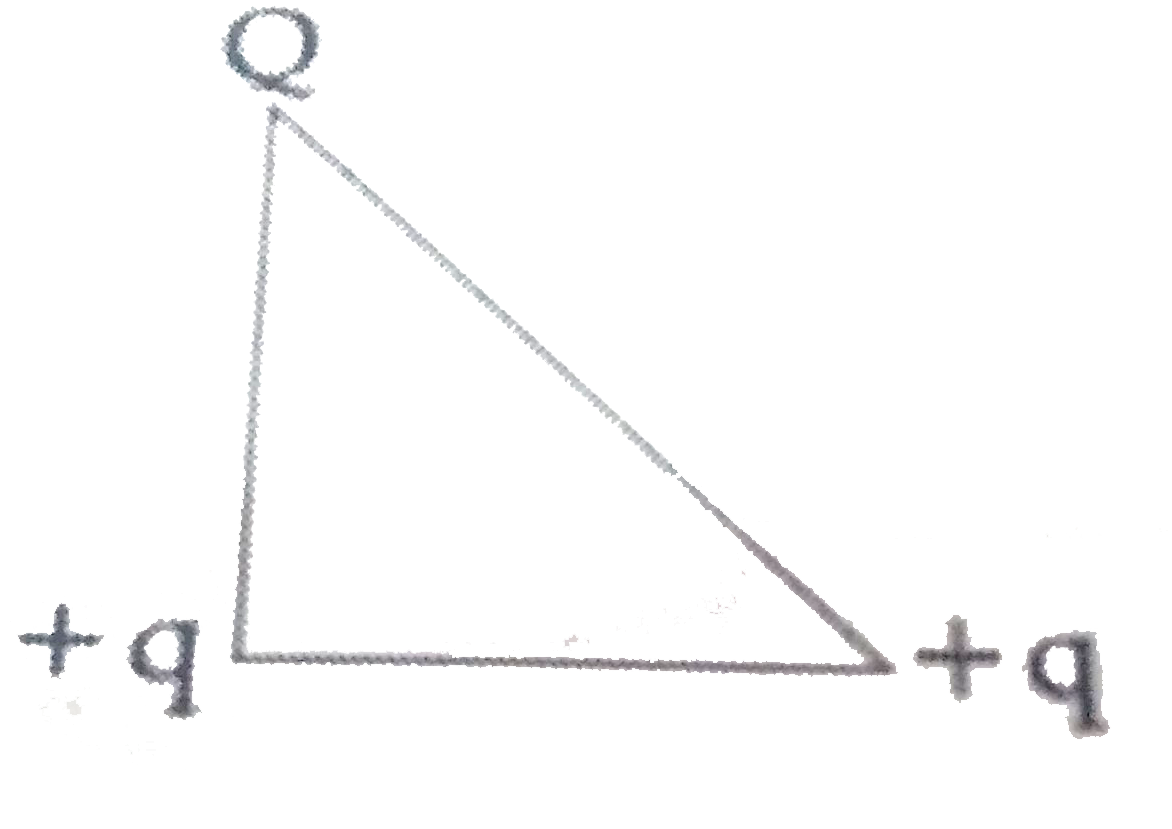
View Solution
Knowledge Check
Three charges Q, +q and +q are placed at the vertices of a right angle triangle (isoscles triangle) as shown. The net electrostatic energy of the configuration is zero, if Q is equal to :
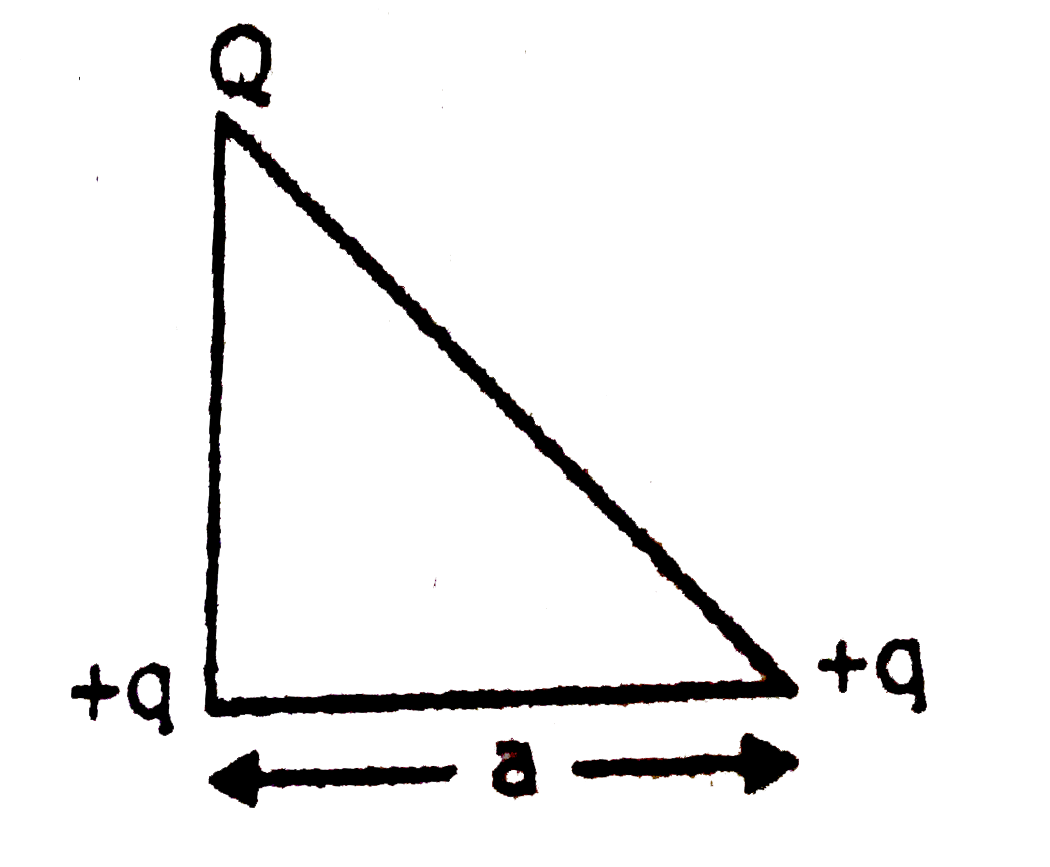 A−q1+√2B−2q2+√2C−2qD+q
A−q1+√2B−2q2+√2C−2qD+qThree charge +q,−q, and +2q are placed at the vertices of a right angled triangle (isosceles triangle)as shown. The net electrostatic energy of the configuration is:
 A−kq2a(√2+1)BKq2a(√2+1)C−Kq2a(√2−1)DNone of these
A−kq2a(√2+1)BKq2a(√2+1)C−Kq2a(√2−1)DNone of theseThree charges Q0,−q and −q are placed at the vertices of an isosceles right angle triangle as in the figure. The net electrostatic potential energy is zero if Q 0 is equal to :
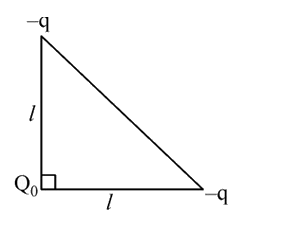 Aq4Bq2√2C√2qD+q
Aq4Bq2√2C√2qD+q
Three charges Q0 - q and q are placed at the vertices of an isosceles right angle triangle as in the future. The net electrostatic potential energy is zero if Q0 is equal to
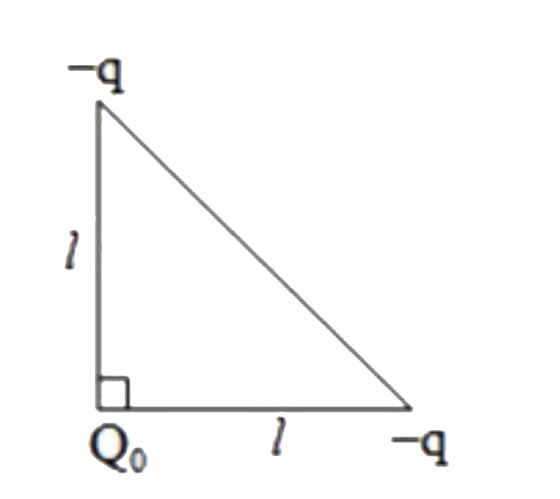
View SolutionThree charges are placed at the vertex of an equilateral triangle as shown in figure. The value of Q, for which the electrostatic potential energy of the system is zero, is
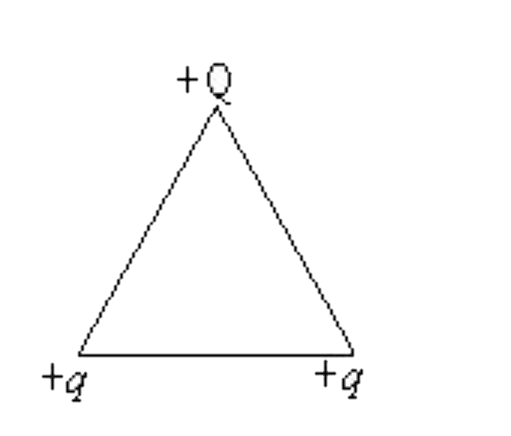
View SolutionThree charges Q,(+q) and (+q) are placed at the vertices of an equilateral triangle of side l as shown in the figure. It the net electrostatic energy of the system is zero, then Q is equal to

View SolutionThree charges +q, +q and -2q are placed at the vertices of an equilareral triagle. What is the dipole moment of the system?
View SolutionThree charges 2q,−q,and−q are located at the vertices of an equilateral triangle. At the center of the triangle,
View Solution