Three charges +q, +q and -2q are placed at the vertices of an equilareral triagle. What is the dipole moment of the system?
√3qa
√3qa2
√2qa
qa2
The correct Answer is:A
To find the dipole moment of the system with charges +q, +q, and -2q placed at the vertices of an equilateral triangle, we can follow these steps:
1. Identify the Configuration:
- Let the vertices of the equilateral triangle be labeled as A, B, and C.
- Place charge +q at vertex A, +q at vertex B, and -2q at vertex C.
2. Consider the Dipole Moment:
- The dipole moment →p is given by the formula:
→p=q⋅→d
where q is the charge and →d is the displacement vector from the negative charge to the positive charge.
3. Calculate Individual Dipole Moments:
- We can treat the -2q charge at C as two -q charges for the purpose of calculating dipole moments:
- From A to C, the dipole moment →p1 can be calculated as:
→p1=q⋅→dAC(from A to C)
- From B to C, the dipole moment →p2 can be calculated as:
→p2=q⋅→dBC(from B to C)
4. Determine the Length of the Sides:
- Let the length of each side of the triangle be L.
5. Calculate the Magnitudes of the Dipole Moments:
- The magnitude of the dipole moment for each charge configuration is:
p1=q⋅L(for charge at A)
p2=q⋅L(for charge at B)
6. Combine the Dipole Moments:
- The dipole moments →p1 and →p2 are at an angle of 60 degrees to each other (since they are from the same vertex to the opposite vertex in an equilateral triangle).
- The resultant dipole moment →Pnet can be calculated using the formula for the resultant of two vectors:
Pnet=√p21+p22+2p1p2cos(60∘)
- Substituting p1=p2=qL:
Pnet=√(qL)2+(qL)2+2(qL)(qL)⋅12
=√(qL)2+(qL)2+(qL)2=√3(qL)2=qL√3
7. Final Result:
- The net dipole moment of the system is:
Pnet=qL√3
- Let the vertices of the equilateral triangle be labeled as A, B, and C.
- Place charge +q at vertex A, +q at vertex B, and -2q at vertex C.
- The dipole moment →p is given by the formula:
→p=q⋅→d
where q is the charge and →d is the displacement vector from the negative charge to the positive charge.
- We can treat the -2q charge at C as two -q charges for the purpose of calculating dipole moments:
- From A to C, the dipole moment →p1 can be calculated as:
→p1=q⋅→dAC(from A to C)
- From B to C, the dipole moment →p2 can be calculated as:
→p2=q⋅→dBC(from B to C)
- Let the length of each side of the triangle be L.
- The magnitude of the dipole moment for each charge configuration is:
p1=q⋅L(for charge at A)
p2=q⋅L(for charge at B)
- The dipole moments →p1 and →p2 are at an angle of 60 degrees to each other (since they are from the same vertex to the opposite vertex in an equilateral triangle).
- The resultant dipole moment →Pnet can be calculated using the formula for the resultant of two vectors:
Pnet=√p21+p22+2p1p2cos(60∘)
- Substituting p1=p2=qL:
Pnet=√(qL)2+(qL)2+2(qL)(qL)⋅12
=√(qL)2+(qL)2+(qL)2=√3(qL)2=qL√3
- The net dipole moment of the system is:
Pnet=qL√3
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Solved examples
Explore 10 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Exercises
Explore 58 Videos
- COMMUNICATION SYSTEMBook:CENGAGE PHYSICSChapter:COMMUNICATION SYSTEMExercise:QUESTION BANK
Explore 19 Videos
- Current ElectricityBook:CENGAGE PHYSICSChapter:Current ElectricityExercise:QUESTION BANK
Explore 40 Videos
Similar Questions
Consider the charges q,q and -q placed at the vertices of an equilateral triangle of each side l. What is the force on each charge ?
View SolutionThree point charges +q, +2q and Q are placed at the three vertices of an equilateral triangle. Find the value of charge Q (in terms of q), so that electric potential energy of the system is zero.
View Solution
Knowledge Check
Three charges 2q,−q,and−q are located at the vertices of an equilateral triangle. At the center of the triangle,
Athe field is zero but potential is nonzero.Bthe field is nonzero but potential is zero.Cboth field and potential are zero.Dboth field and potential are nonzero.Three charges Q,(+q) and (+q) are placed at the vertices of an equilateral triangle of side l as shown in the figure. It the net electrostatic energy of the system is zero, then Q is equal to
 A(−q2)B(−q)C(+q)DZero
A(−q2)B(−q)C(+q)DZeroThree positive charges of equal magnitude q are placed at the vertices of and equilateral triangle of side l. How can the system of charges be placed in equilibrium?
Aby placing a charge Q=−q/√3 at the centroid of the triangleBby placing a charge Q=q/√3 at the centroid of the triangleCby placing a charge Q=q at the centroid of the triangleDby placing a charge Q=−q at the centroid of the triangle
Three point charges q,−4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the Fig. Obtain the experssion for the magnitude of the resultant electric force acting on the charge q.
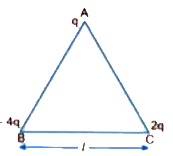
View Solution(a) Three point charges q,-4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q.
(b) Find out the amount of the work done to separate the charges at infinite distance.

View Solution(a) Three point charges q,-4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q.
(b) Find out the amount of the work 4one to separate the charges at infinite distance.

View SolutionThree charge +Q,+Q and −Q are placed at the corners of an equilateral triangle. The ratio of the force on a positive charge to the force on the negative charge will be equal to
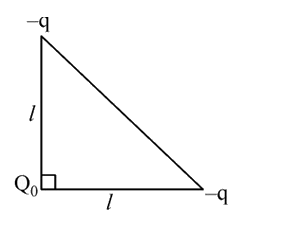
View SolutionThree charges Q0,−q and −q are placed at the vertices of an isosceles right angle triangle as in the figure. The net electrostatic potential energy is zero if Q 0 is equal to :
View Solution

