A small particle of mass m and charge-q is placed at point P on the axis of uniformly chrarged ring and releases. If R>>x, the particle will undergo oscillations along the axis of symmetry with an angurlar frequency that isequal to-
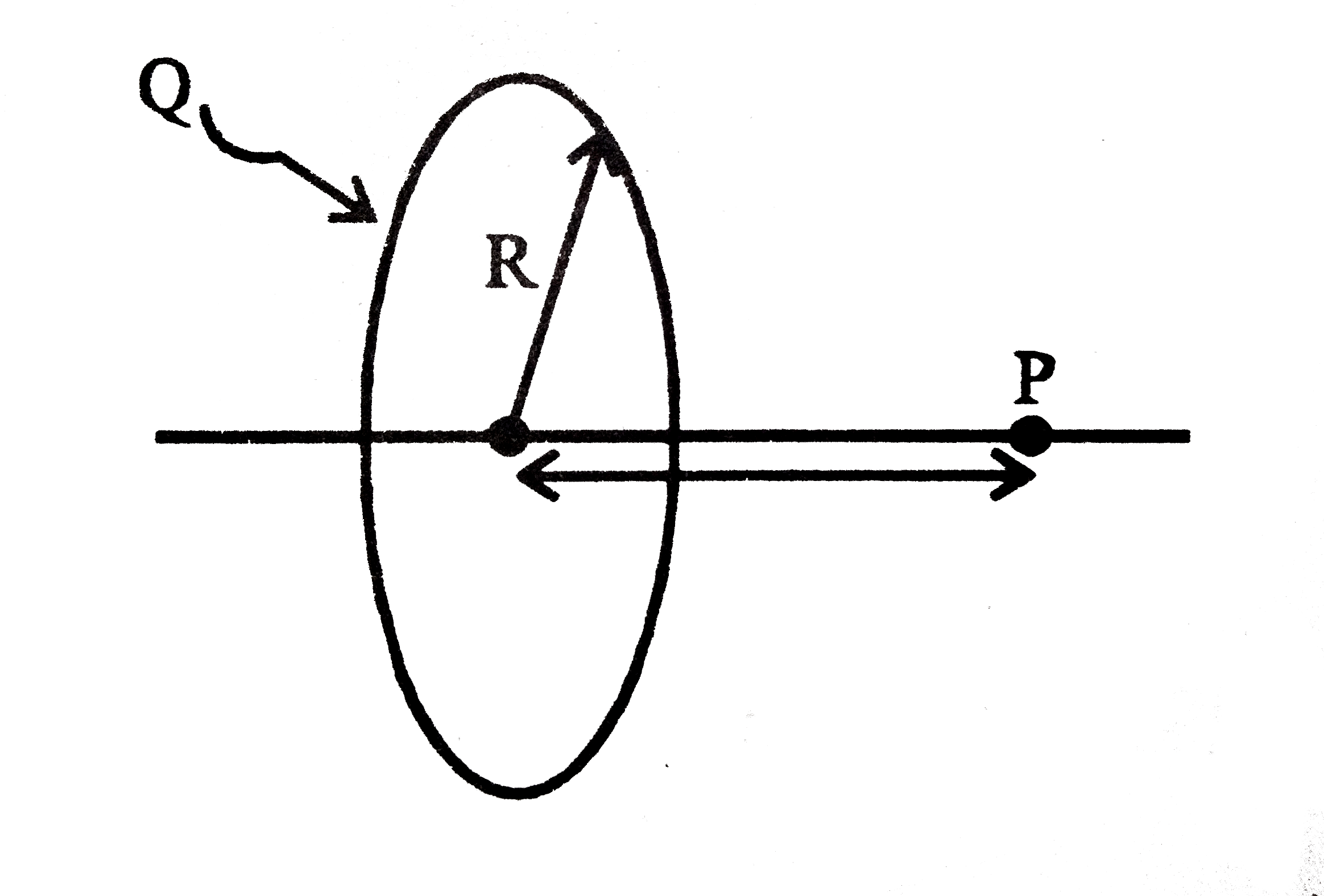 .
.
√qQ4πɛ0mR3
√qQ4πɛ0mR4
√qQ4πɛ0mR3
√qQ4πɛ0mR4
The correct Answer is:A
Ep=KQx(R2+x2)3/2
FR=−qE=−14π∈0Qqx(R2+x2)3/2

since R>.X so F−R=−14π∈0QqR3.x
Compare with F+R=−Kx,K=Qq4π∈0R3
ω=√Km⇒ω=√Qq4π∈0mR3.
Similar Questions
A particle of mass m and charge +q approaches from a very large distance towards a uniformly charged ring ofradius Rand charge, mass same as that of particle, with initial velocity v0 along the axis of the ring as shown in the figure-1.420. What is the closest distance of approach between the ring and the particle? Assume the space to be gravity free and frictionless :

View SolutionThe maximum electric field intensity on the axis of a uniformly charged ring of charge q and radius R is at a distance x from the centre of the ring.The value of x is
View Solution
Knowledge Check
A particle of mass m and charge q is placed at rest in a uniform electric field E and then released, the kinetic energy attained by the particle after moving a distance y will be
Aq2EyBqEyCaE2yDqEy2The maximum electric field intensity on the axis of a uniformly charged ring of charge q and radius R will be
A14πε0q3√3R2B14πε02q3R2C14πε02q3√3R2D14πε03q2√2R2A charged particle of charge q moving with the velocity v, enters along the axis of a solenoid carrying a current. If B is the magnetic induction along the axis of the solenoid then the force acting on the charged particle will be
AqvBBless then qvBCzeroDmore than qvB
A charge particle of mass m and charge q is projected with velocity v along y-axis at t=0.

Find the velocity vector and position vector of the particle →v(t)and→r(t) in relation with time.
View SolutionA particle of mass m and charge −Q is constrained to move along the axis of a ring of radius a. The ring carries a uniform charge density +λ along its length. Initially, the particle is in the centre of the ring where the force on it is zero. Show that the period of oscillation of the particle when it is displaced slightly from its equilibrium position is given by
T=2πsq√2ε0ma2λQ
View SolutionPositive charge Q is distributed uniformly over a circular ring of radius R. A particle having a mass m and a negative charge q, is placed on its axis at a distance x from the centre. Find the force on the particle. Assuming x ltltR, find the time period of oscillation of the particle if it is released from there.
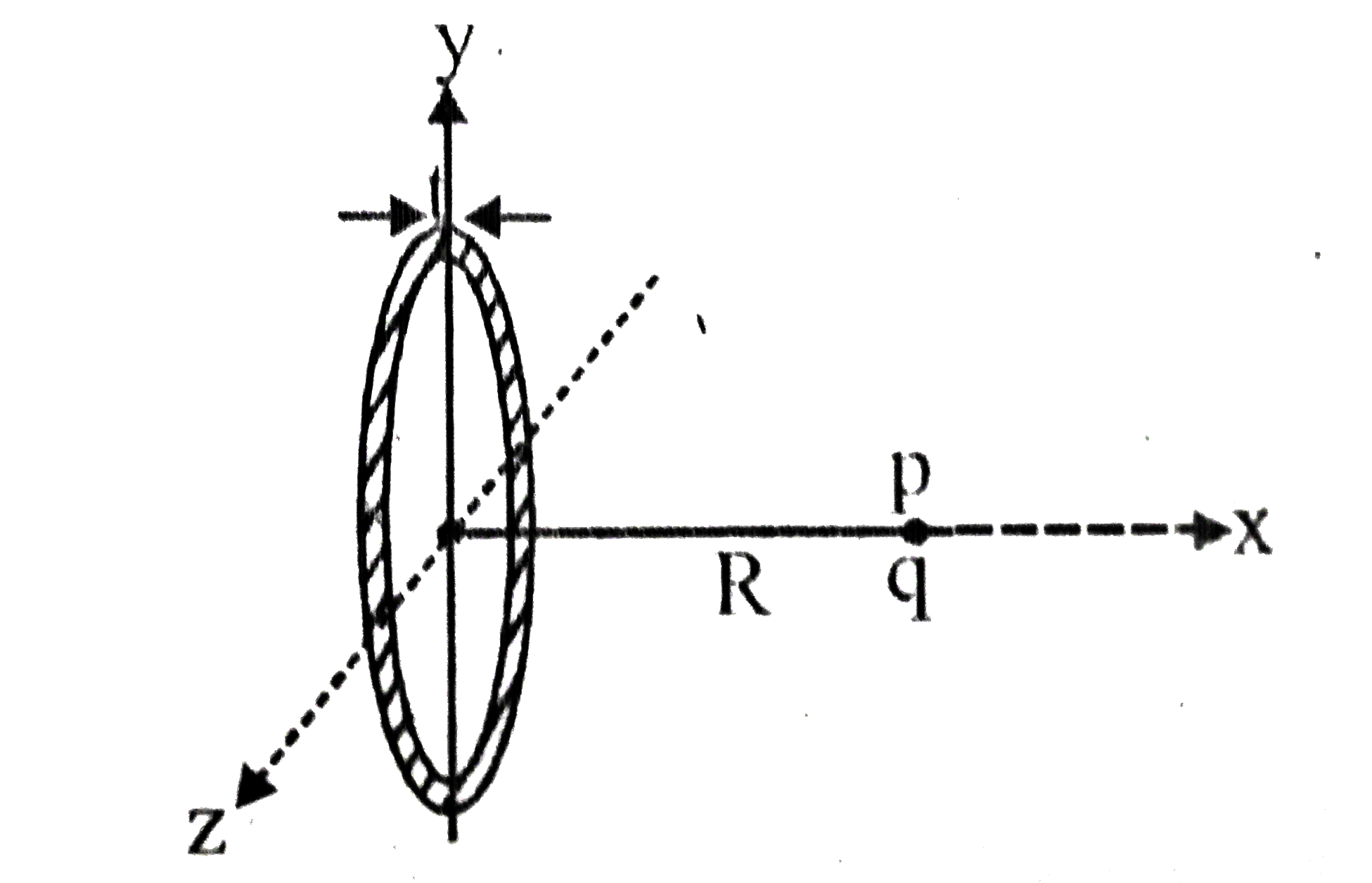
View SolutionA charge q is placed at the point P as shown in figure on the axis of the ring of elemental thickness 't' and radius R then flux through the ring is :-
View SolutionWhich statement is true :-
(i) A ring of radius R carries a uniformly distributed charge +Q. A point charge -q is placed on the axis of the ring at a distance 2R from the centre of the ring and released from rest. The particle executes a smiple harmonic motion along the axis of the ring.
(ii) Electrons move from a region of higher potential to that of lower potential
View Solution
