A cell of e.m.f. 2V and internal resistance 0.5Ω is connected across a resistor R. The current that flows is same as that, when a cell of e.m.f. 1.5V and internal resistance 0.3Ω is connected across the same resistor. Then
R=0.3Ω
R=0.6Ω
R=0.5Ω
R=0.75Ω
The correct Answer is:A
To solve the problem step by step, we will use Ohm's law and the concept of equivalent resistance in series circuits.
Step 1: Identify the components of the first circuit
We have a cell with an e.m.f. E1=2V and internal resistance r1=0.5Ω connected across a resistor R. The current I flowing through the circuit can be expressed using Ohm's law:
I=E1R+r1
Substituting the values:
I=2R+0.5
Step 2: Identify the components of the second circuit
In the second circuit, we have a cell with an e.m.f. E2=1.5V and internal resistance r2=0.3Ω connected across the same resistor R. The current I flowing through this circuit is:
I=E2R+r2
Substituting the values:
I=1.5R+0.3
Step 3: Set the currents equal
Since the current I is the same in both circuits, we can set the two equations equal to each other:
2R+0.5=1.5R+0.3
Step 4: Cross-multiply to eliminate the fractions
Cross-multiplying gives us:
2(R+0.3)=1.5(R+0.5)
Step 5: Expand both sides
Expanding both sides results in:
2R+0.6=1.5R+0.75
Step 6: Rearrange the equation
Rearranging the equation to isolate R:
2R−1.5R=0.75−0.6
This simplifies to:
0.5R=0.15
Step 7: Solve for R
Now, divide both sides by 0.5 to find R:
R=0.150.5=0.3Ω
Conclusion
The value of the resistor R is 0.3Ω.
---
We have a cell with an e.m.f. E1=2V and internal resistance r1=0.5Ω connected across a resistor R. The current I flowing through the circuit can be expressed using Ohm's law:
In the second circuit, we have a cell with an e.m.f. E2=1.5V and internal resistance r2=0.3Ω connected across the same resistor R. The current I flowing through this circuit is:
Since the current I is the same in both circuits, we can set the two equations equal to each other:
Cross-multiplying gives us:
Expanding both sides results in:
Rearranging the equation to isolate R:
Now, divide both sides by 0.5 to find R:
The value of the resistor R is 0.3Ω.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - NIKITA PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Multiple Choice Questions
314 Videos
- COMMUNICATION SYSTEMSBOOK - NIKITA PUBLICATIONCHAPTER - COMMUNICATION SYSTEMSEXERCISE - Multiple Choice Questions (Examples for Practice)
8 Videos
- ELASTICITYBOOK - NIKITA PUBLICATIONCHAPTER - ELASTICITYEXERCISE - MCQ
314 Videos
Similar Questions
Knowledge Check
A cell of emf 2 V and internal resistance 0.1Ω is connected with a resistance of 3.9Ω The voltage across the cell terminal will be
A1.95VB1.90VC0.50VD2.00VA cell of emf 2.0 V and internal resistance 0.1 Ω is connected with a resistance of 3.9Ω. The voltage across the cell terminals will be
A0.50 VB1.90 VC1.95 VD2.0 VA battery having e.m.f. 5 V and internal resistance 0.5Ω is connected with a resistance of 4.5Ω then the voltage at the terminals of battery is
A4.5 VB4 VC0 VD2 V
A battery of emf 12V and internal resistance 2Ω is connected two a 4Ω resistor. Show that the a voltmeter when placed across cell and across the resistor in turn given the same reading
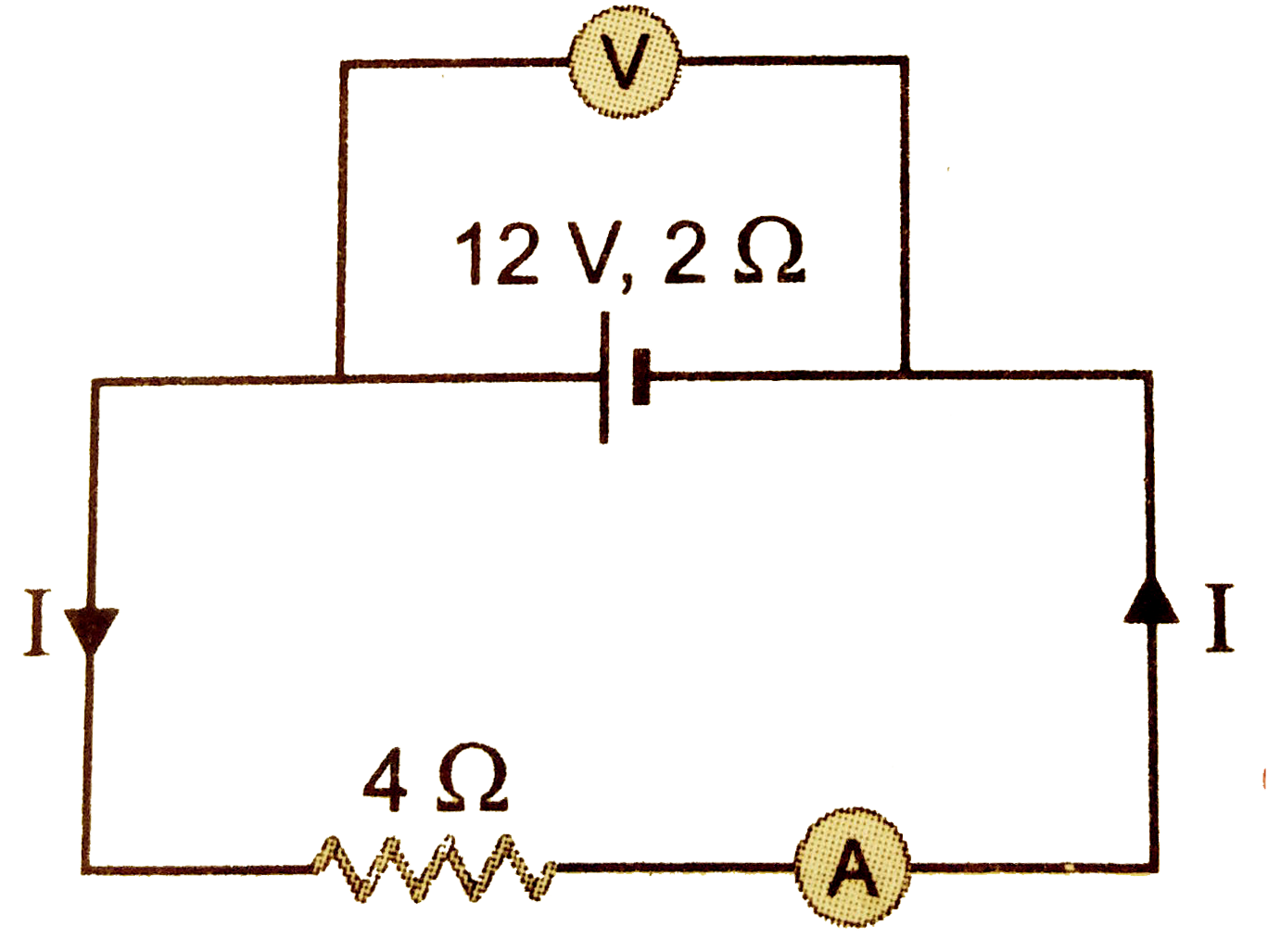
View SolutionA battery having e.m.f. 5 V and internal resistance 0.5Ω is connected with a resistance of 4.5Ω then the voltage at the terminals of battery is
View SolutionA battery of emf 10 V and internal resistance 3Ωis connected to a resistor. The current in the circuit is 0.5 A . The terminal voltage of the battery when the circuit is closed is
View SolutionA cell of e.m.f. 2 V and internal resistance 2Ω and an external resistance 18Ω forms closed circuit. The current through the circuit is
View Solution4 cells each of emf 2 V and internal resistance of 1Ω are connected in parallel to a load resistor of 2Ω. Then the current through the load resistor is
View Solution
