Two particles of masses 2 kg and 3 kg are separated by 5 m. Then moment of inertia of the system about an axis passing through the centre of mass of the system and perpendicular to the line joining them is
10kgm2
20kgm2
30kgm2
40kgm2
The correct Answer is:C
To find the moment of inertia of the system about an axis passing through the center of mass and perpendicular to the line joining the two particles, we can follow these steps:
Step 1: Identify the masses and the distance between them
We have two particles:
- Mass m1=2kg
- Mass m2=3kg
- Distance d=5m
Step 2: Calculate the position of the center of mass (CM)
The position of the center of mass xCM for two particles can be calculated using the formula:
xCM=m1x1+m2x2m1+m2
Assuming m1 is at position x1=0 and m2 is at position x2=5m:
xCM=(2kg⋅0)+(3kg⋅5m)2kg+3kg=15kg m5kg=3m
Step 3: Calculate the distances from the center of mass to each mass
Now, we need to find the distances from the center of mass to each mass:
- Distance from m1 to xCM:
r1=xCM−x1=3m−0m=3m
- Distance from m2 to xCM:
r2=x2−xCM=5m−3m=2m
Step 4: Use the formula for moment of inertia about the center of mass
The moment of inertia I about the center of mass is given by:
I=m1r21+m2r22
Substituting the values:
I=(2kg⋅(3m)2)+(3kg⋅(2m)2)
Calculating each term:
I=(2kg⋅9m2)+(3kg⋅4m2)
I=18kg m2+12kg m2=30kg m2
Final Answer
The moment of inertia of the system about the axis passing through the center of mass and perpendicular to the line joining them is:
30kg m2
We have two particles:
- Mass m1=2kg
- Mass m2=3kg
- Distance d=5m
The position of the center of mass xCM for two particles can be calculated using the formula:
xCM=m1x1+m2x2m1+m2
Assuming m1 is at position x1=0 and m2 is at position x2=5m:
xCM=(2kg⋅0)+(3kg⋅5m)2kg+3kg=15kg m5kg=3m
Now, we need to find the distances from the center of mass to each mass:
- Distance from m1 to xCM:
r1=xCM−x1=3m−0m=3m
- Distance from m2 to xCM:
r2=x2−xCM=5m−3m=2m
The moment of inertia I about the center of mass is given by:
I=m1r21+m2r22
Substituting the values:
I=(2kg⋅(3m)2)+(3kg⋅(2m)2)
Calculating each term:
I=(2kg⋅9m2)+(3kg⋅4m2)
I=18kg m2+12kg m2=30kg m2
The moment of inertia of the system about the axis passing through the center of mass and perpendicular to the line joining them is:
30kg m2
Topper's Solved these Questions
Similar Questions
Three identical spheres each of mass M and radius R are arranged in a row touching each other and their centres collinear.The moment of inertia of the system about an axis passing through the centre of the middle sphere and perpendicular to the line joining their centres is "
View Solutionfind moment of inertia about an axis yy which passes through the centre of mass of the two particle system as shown
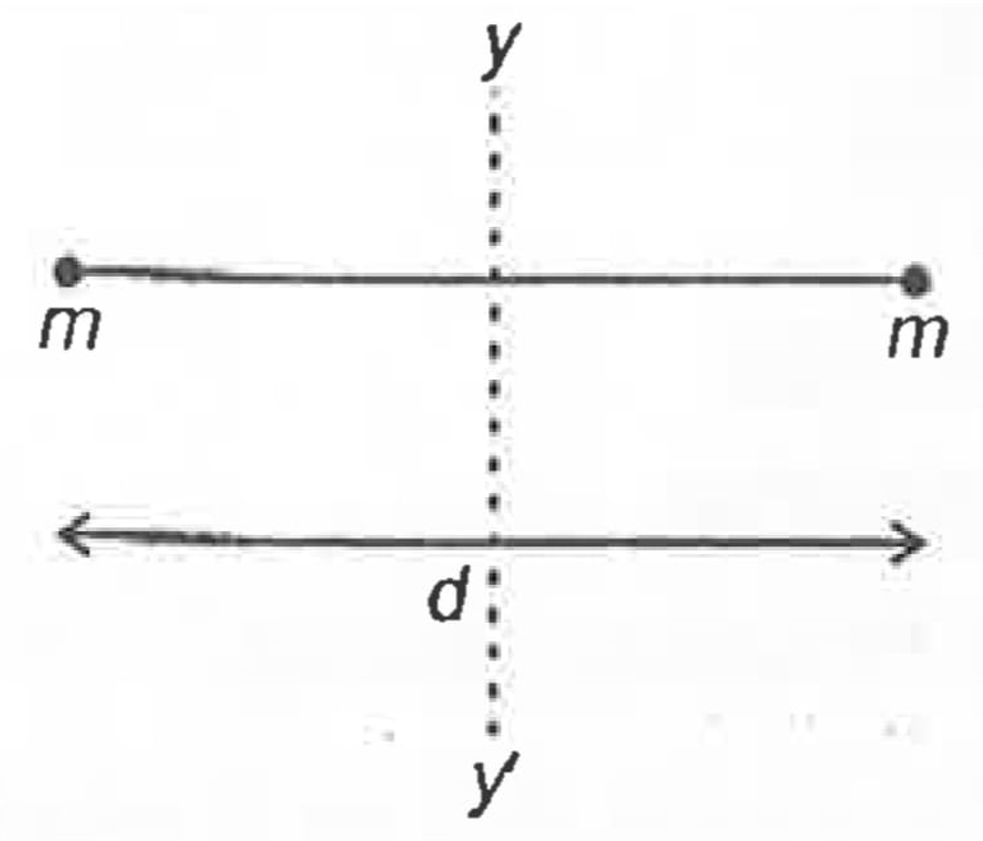
View Solution
Knowledge Check
Two particles of masses m1 and m2 are separated by a distance 'd'. Then moment of inertia of the system about an axis passing through centre of mass and perpendicular the line joining them is
A(m1m2m1+m2)d22B(m1m2m1+m2)dC(m1m2m1+m2)d2D(2m1m2m1+m2)d2Two point masses m and 3m are placed at distance r. The moment of inertia of the system about an axis passing through the centre of mass of system and perpendicular to the joining the point masses is
A35mr2B34mr2C32mr2D67mr2Two partcles of masses 1 kg and 2 kg are placed at a distance of 3 m. Moment of inertia of the particles about an axis passing through their centre of mass and perpedicular to the line joining them is (in kg−m2)
A6B9C8D12
The moment of inertia of a square plate of mass 4kg and side 1m about an axis passing through its centre and perpendicular to its plane is
View SolutionDoes centre of mass of a system of two particles lie on the line joining the particles ?
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionTwo spheres each mass M and radius R are connected with massless rod of length 2R . Then moment of inertia of the system about an axis passing through the centre of one of sphere and perpendicular to the rod will be
View SolutionTwo rods each of mass m and length l are joined at the centre to form a cross. The moment of inertia of this cross about an axis passing through the common centre of the rods and perpendicular to the plane formed by them is :
View Solution
