Question

ऐम्पियर का परिपथीय नियम क्या है ? लिखिए तथा सिद्धांत दीजिए ।

Explanation

इस नियम के अनुसार , निर्वात में किसी बंद परिपथ के लिये चुंबकीय क्षेत्र `vec(B)` का रेखीय समाकलन उस पथ से घिरी कुल धारा का `mu_(0)`गुना होता है । गणितीय रूप में इसे निम्न समीकरण द्वारा व्यक्त किया जाता है -
` oint vec(B) . vec(dl) = mu_(0)I`
जहाँ `mu_(0)`हवा या निर्वात की चुंबकशीलता है ।
व्युत्पत्ति - चित्र के अनुसार माना कि MN एक लम्बा ऋजुरेखीय चालक है जिसमे M से N कि दिशा में धारा I प्रवाहित हो रही है । अतः इस चालक के चारों ओर चुंबकीय क्षेत्र उत्पन्न हो जायेगा । इस क्षेत्र की डीसी लंबवत तल में ( चालक के) चुंबकीय बल रेखाएँ सकेंद्रीय वृतों के रूप में होगी जिनका केंद्र चालक पर स्थित होगा ।

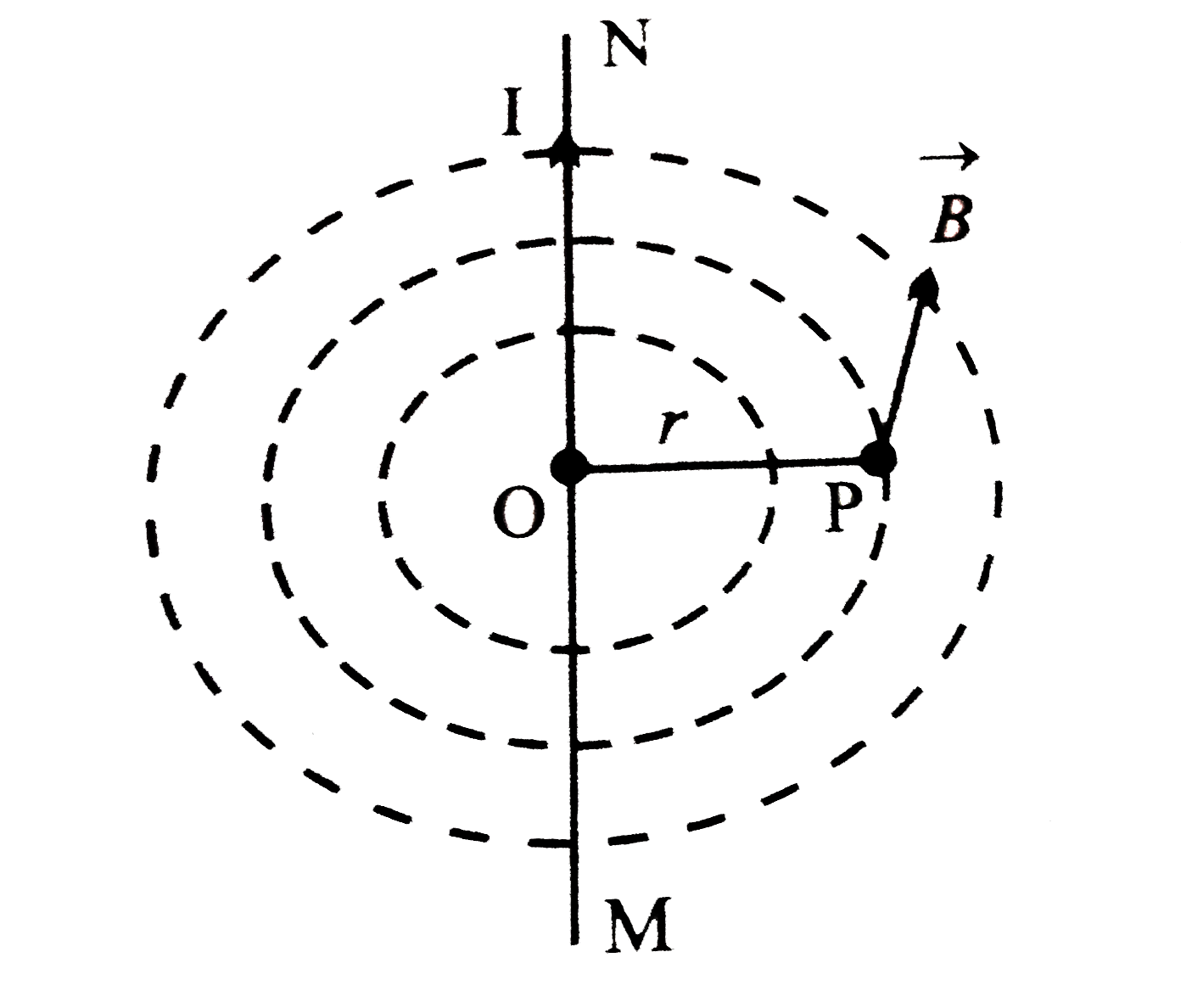
अब यदि चालक से r दूरी पर स्थित किसी बिंदु P पर उत्पन्न चुंबकीय क्षेत्र B हो , तो
`B = mu_(0)/(4pi) (2I)/r ` ....(1)
इस क्षेत्र की दिशा बिंदु P से वृत्त पर खींची गई स्पर्श रेखा के अनुदिश होगी । बिंदु P पर एक अवयव `vec(dl)`लिया अतः `vec(B)"और "vec(dl)`एक ही दिशा में होंगे । अतः सम्पूर्ण बंद वक्र ( वृत्त ) के लिये चुंबकीय क्षेत्र `vec(B)` का रेखीय समाकलन
`oint vec(B) .vec(dl) = oint Bdl cos 0^(@) = oint Bdl`
` = B oint dl = B * 2 pi r` ....(2)
क्योंकि `= oint dl = 2 pi r ` होता है । अतः समीकरण (1) और(2) से ,
`oint vec(B) .vec(dl) = mu_(0)/(4pi) * (2l)/r 2 pi r`
या ` oint vec(B) . vec(dl) = mu_(0) I` ....(3)
यही ऐम्पियर का परिपथीय नियम है ।