Question

किस वृत्ताकार धारावाही कुंडली कि अक्ष पर स्थित किसी बिंदु पर चुम्बकीय क्षेत्र की तीव्रता का व्यंजक ज्ञात कीजिए ।

Explanation

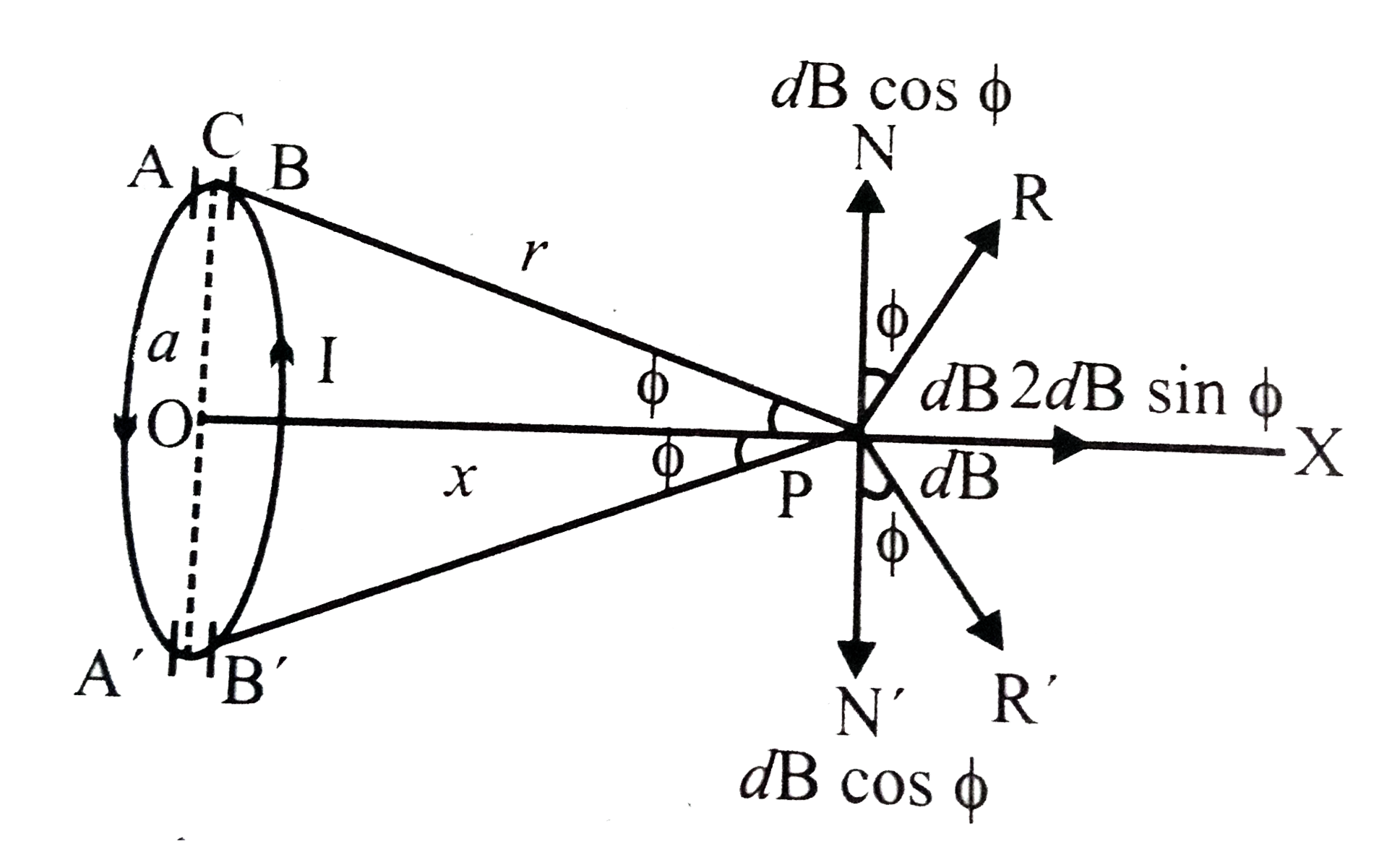
चित्र के अनुसार , माना कि a त्रिज्या की एक कुंडली है , जिसमे I धारा तीर की दिशा में प्रवाहित हो रही है । कुंडली के केंद्र O से xदूरी पर स्थित बिंदु P पर चुम्बकीय क्षेत्र ज्ञात करना है । माना की कुंडली का तल कागज के तल के लंबवत तथा उसका अक्ष OP कागज के तल पर स्थित है । कुंडली को अनेक अल्पांशों में विभक्त किया । माना कि कुंडली के ठीक ऊपरी सिरे पर dl लम्बाई का एक अल्पांश AB है । इस अल्पांश से बिंदु P कि दूरीr है ।अतः इस अल्पांश के कारण बिंदु P पर चुंबकीय क्षेत्र
`dB = mu_(0)/(4pi) (Idl sin theta)/r^(2)`

जहाँ `theta`अल्पांश तथा अल्पांश को बिंदु P से मिलाने वाली रेखा के बीच कोण है , अतः `theta = 90^(@)` होगा । अतः उपरोक्त समीकरण से ,
`dB = mu_(0)/(4pi) (Idl sin 90^(@))/r^(2)`
` = mu_(0)/(4pi) (Idl)/r^(2) ` ...(1)
इस क्षेत्र dB कि दिशा अल्पांश AB और अल्पांश को P से मिलाने वाली रेखा के तल के लंबवत PR दिशा में होगी । इसी प्रकार कुंडली के ठीक नीचे सिरे पर उतनी ही लम्बाई dlका एक दूसरा अल्पांश A'B' लें तो इस अल्पांश के कारण बिंदु P पर चुम्बकीय क्षेत्र निम्न होगा -
` dB = mu_(0)/(4pi) (Idl)/r^(2)`
इन दोनों अल्पांशों के कारण चुंबकीय क्षेत्र के अक्ष के लंबवत दिशा में अवयव `dB cos phi ` एक - दूसरे के विपरीत दिशा (PN व PN')में होने के कारण एक - दूसरे को नष्ट करेंगे , जबकि क्षैतिज अवयव अक्ष OP कि दिशा में होने के कारण जुड़ जायेंगे अर्थात अल्पांशों AB एवं A'B' के कारण बिंदु P पर परिणामी तीव्रता `dB sin phi + dB sin phi` होगी ।
अतः स्पष्ट है कि वृत्तीय कुंडली के सभी अल्पांशों के कारण OP के लंबवत दिशा में चुंबकीय क्षेत्र के घटक सम्मुख अल्पांशों द्वारा नष्ट हो जायेंगे , जबकि OP दिशा के अवयव जुड़ जायेंगे । अतः सम्पूर्ण धारावाही कुंडली के कारण बिंदु पर परिणामी तीव्रता
`B = SigmadB sin phi = oint d B sin phi`
` = oint mu_(0)/(4pi) (Idl)/r^(2) sin phi` ...(2)
परन्तु `Delta OAP" में, "sin phi = a/r ` अतः समीकरण (2) से ,
`B = oint mu_(0)/(4pi) (Idla)/r^(2) * bar(r) = oint mu_(0)/(4pi) (Ia)/r^(3) oint dl `
परन्तु `ont dl = 2 pi a`
= कुंडली की परिधि
` B = mu_(0)/(4pi) * (Ia)/r^(3) 2 pi a `
` = mu_(0)/( 4pi) * ( 2 pi I a^(2))/r^(3) ` ...(3)
अब समकोण `Delta COP` में ,
`r^(2) = a^(2) + x^(2) " या " = (a^(2) + x^(2))^(1//2) `
` r^(3) = (a^(2) + x^(2))^(3//2)`
अतः समीकरण (3) में `r^(3)`के मान को रखने पर ,
` B = mu_(0)/(4pi) * (2 pi I a^(2))/((a^(2) + x^(2))^(3//2))`
अब यदि वृत्तीय धारावाही कुंडली में चक्करों की संख्या n हो , तो
` B = mu_(0)/(4pi) . (2pinIa^(2))/((a^(2) + x^(2))^(3//2))`
` = 10^(-7) . ( 2 pi n I a^(2)) /((a^(2) + x^(2))^(3//2))`
यदि धारावाही वृत्तीय कुंडली की अक्ष पर स्थित किसी बिंदु पर चुम्बकीय क्षेत्र का सूत्र है ।