The Q value of a nuclear reaction
A+b=C+d is defined by Q=[mA+mb−mC−md]c2 where the masses refer to the respective nuclei. Determine form the given data the Q value of the following reactions and state whether the reactions are exothermic of endothermic.
(i) .1H1+.1H3→.1H2+.1H2
(ii) .6C12+.6C12→.10Ne20+.2He4
Atomic masses are given to be
m(.1H2)=2.014102u,m(.1H3)=3.016049u,m(.6C12)=12.000000u,m(.10Ne20)=19.992439u
To determine the Q value for the given nuclear reactions and classify them as exothermic or endothermic, we will follow the formula provided:
Q=(mA+mb−mC−md)c2
Where:
- mA and mb are the masses of the reactants,
- mC and md are the masses of the products,
- c is the speed of light (but we will use the mass-energy equivalence in MeV).
1. Identify the masses:
- mA=m(1H1)=1.007825u
- mb=m(1H3)=3.016049u
- mC=m(1H2)=2.014102u (two 1H2 nuclei)
- Therefore, total mass of products = 2×m(1H2)=2×2.014102u=4.028204u
2. Calculate the Q value:
Q=(mA+mb−2×mC)c2
Q=(1.007825+3.016049−4.028204)c2
Q=(4.023874−4.028204)c2
Q=−0.004330u⋅c2
3. Convert to MeV:
Using the conversion 1u⋅c2≈931.5MeV:
Q=−0.004330×931.5MeV≈−4.03MeV
4. Determine the nature of the reaction:
Since Q<0, the reaction is endothermic (energy is absorbed).
---
(ii) Reaction: 6C12+6C12→10Ne20+2He4
1. Identify the masses:
- mA=m(6C12)=12.000000u (two 6C12 nuclei)
- Therefore, total mass of reactants = 2×m(6C12)=2×12.000000u=24.000000u
- mC=m(10Ne20)=19.992439u
- md=m(2He4)=4.002603u
2. Calculate the Q value:
Q=(2×mA−mC−md)c2
Q=(24.000000−19.992439−4.002603)c2
Q=(24.000000−23.995042)c2
Q=0.004958u⋅c2
3. Convert to MeV:
Q=0.004958×931.5MeV≈4.61MeV
4. Determine the nature of the reaction:
Since Q>0, the reaction is exothermic (energy is released).
Summary of Results:
- For reaction (i): Q≈−4.03MeV (endothermic)
- For reaction (ii): Q≈4.61MeV (exothermic)
---
- mA and mb are the masses of the reactants,
- mC and md are the masses of the products,
- c is the speed of light (but we will use the mass-energy equivalence in MeV).
- mA=m(1H1)=1.007825u
- mb=m(1H3)=3.016049u
- mC=m(1H2)=2.014102u (two 1H2 nuclei)
- Therefore, total mass of products = 2×m(1H2)=2×2.014102u=4.028204u
Q=(mA+mb−2×mC)c2
Q=(1.007825+3.016049−4.028204)c2
Q=(4.023874−4.028204)c2
Q=−0.004330u⋅c2
Using the conversion 1u⋅c2≈931.5MeV:
Q=−0.004330×931.5MeV≈−4.03MeV
Since Q<0, the reaction is endothermic (energy is absorbed).
- mA=m(6C12)=12.000000u (two 6C12 nuclei)
- Therefore, total mass of reactants = 2×m(6C12)=2×12.000000u=24.000000u
- mC=m(10Ne20)=19.992439u
- md=m(2He4)=4.002603u
Q=(2×mA−mC−md)c2
Q=(24.000000−19.992439−4.002603)c2
Q=(24.000000−23.995042)c2
Q=0.004958u⋅c2
Q=0.004958×931.5MeV≈4.61MeV
Since Q>0, the reaction is exothermic (energy is released).
- For reaction (i): Q≈−4.03MeV (endothermic)
- For reaction (ii): Q≈4.61MeV (exothermic)
Topper's Solved these Questions
- ATOMS AND NUCLEIBOOK - PRADEEPCHAPTER - ATOMS AND NUCLEIEXERCISE - (II) very short answer 16
1 Videos
- ATOMS AND NUCLEIBOOK - PRADEEPCHAPTER - ATOMS AND NUCLEIEXERCISE - (I) Short Answer questions 1
1 Videos
- COMMUNICATION SYSTEMSBOOK - PRADEEPCHAPTER - COMMUNICATION SYSTEMSEXERCISE - MODEL TEST PAPER-2
9 Videos
Similar Questions
The Q-value of a nuclear reaction A + b → C + d is defined by Q=[mA+mb−mC−md]c2
where the masses refer to the respective nuclei. Determine from the given data the Q-value of following reactions and state whether the reactions are exothermic or endothermic.
(i) 11H+ 31H(→) 21H+ 21H (ii) 126C+ 126C(→) 2010Ne+ 42He
Atomic masses are given to be m( 21H)=2.014102u, m( 31H)=3.016049u, m( 126C)=12.000000u, m( 2010Ne)=19.992439u.
View SolutionCalculate the Q-values of the following fusion reactions:
(a)_1^2H+_12H→_1^3H+_11H.
_1^2H+_12H→_2^3(He)+n<br>_12H+_1^3H rarr _24(He)+n.
Atomic masses are m(_1^2H)=2.014102 u, m(_13H)=3.016049u,m(_2^3(He))=3.016029 u, m(_24(He))=4.002603u.
View Solution
Knowledge Check
The cell reaction for the given cell is spontaneous if:
Pt,H2(P1atm)∣∣H+(1M)∣∣H2(P2atm),PtAP1>P2BP1<P2CP1=P2DP2=1atmGiven the reactions and data below, what is the K value for this electrochemical cell?
Cu|CuNO(3)(1.0M)|∣∣I−(1.0M),I2(1.0M)∣∣Pt at 25∘C.
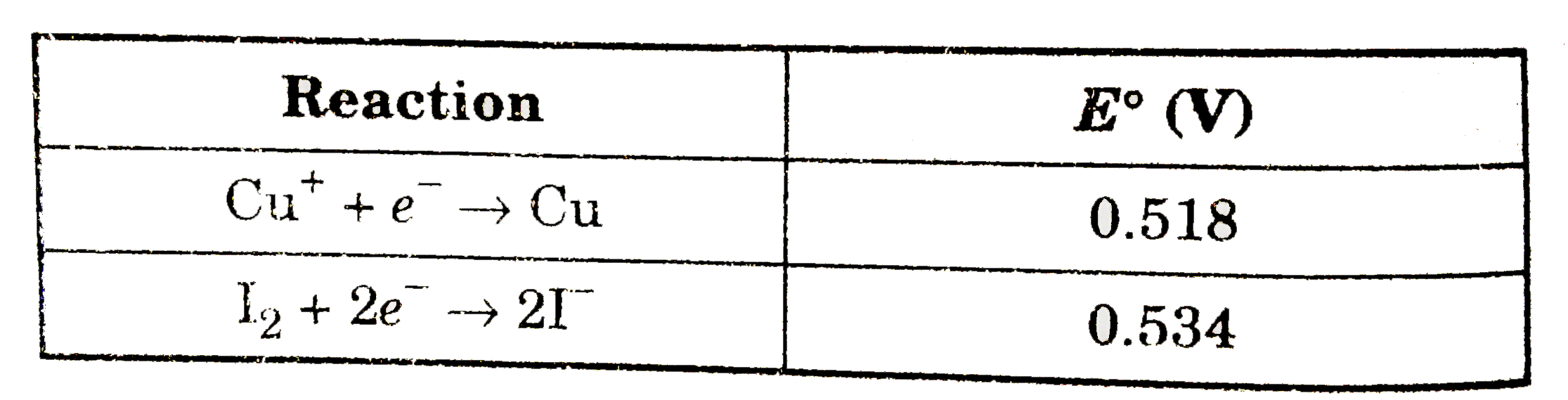 A0.288B1.86C2.23D3.48
A0.288B1.86C2.23D3.48
Calculate the energy of the following nuclear reaction:
.1H2+.1H3→.2He4+.0n1+Q
Given: m(.1H2)=2.014102u,m(.1H3)=3.016049u,m(.2He4)=4.002603u,m(.0n1)=1.008665u
View SolutionCalculate the energy released in the given reaction:
6C12+6C12→10Ne20+2He4
Given atomic masses are as follows:
MHe=4.002603u,MNe=19.992439u,
Mc=12.0000u
View SolutionFind the Q value of the reaction P+.7Li→.4He+.4He. Determine whether the reaction is exothermic or endothermic. The atomic masses of .1H,.4He and .7Li are 1.007825u,4.002603u, and 7.016004u, respectively.
View SolutionCalculate the Q - value of the reaction
.1H2+.1H2→.1H3+.1H1
m(.1H2)=2.014103amum(.1H3)=3.016049amum(.1H1=1.007825 amu
View SolutionDistinguish between nuclear fission and fusion. Show how in both these processes energy is …… Calculate the energy release in MeV in the deuteriumtritium fusion reaction:
.21H+.31H→.31He+n
Using the data.
m(.21H)=2.014102um(.31H)=3.016049um(.31He)=4.002603umn=1.008665ulu=931.5MeV/c2
View Solution(a) Distinguish between nuclear fission and fusion. Show how in both these processes energy is released.
(b) Calculate the energy release in MeV in the deuterium-tritium fusion reaction :
21H+ 31H→ 42He+n
Using the data: m( 21H)=2.014102u,m( 31H)=3.016049u,m( 42He)=4.002603u,mn=1.008665u and 1u=931.5MeVc2.
View Solution
