A jar of height h is filled wih a transparent liquid of refractive index , Fig. At the centre of the jar on the botom surface is a dot. Find the minimum diameter of a disc, such that when placed on the top surface symmetrically about the centre, the dot is invisible.
 .
.
In Fig. is a on dot the bottom surface of a jar of height , filled with a transparent liquid of refraactive index . is diameter of a disc such that when placed on the top surface, symmetrically about the centre, the dot is invisible. This would happen when rays suffer total internal reflection.
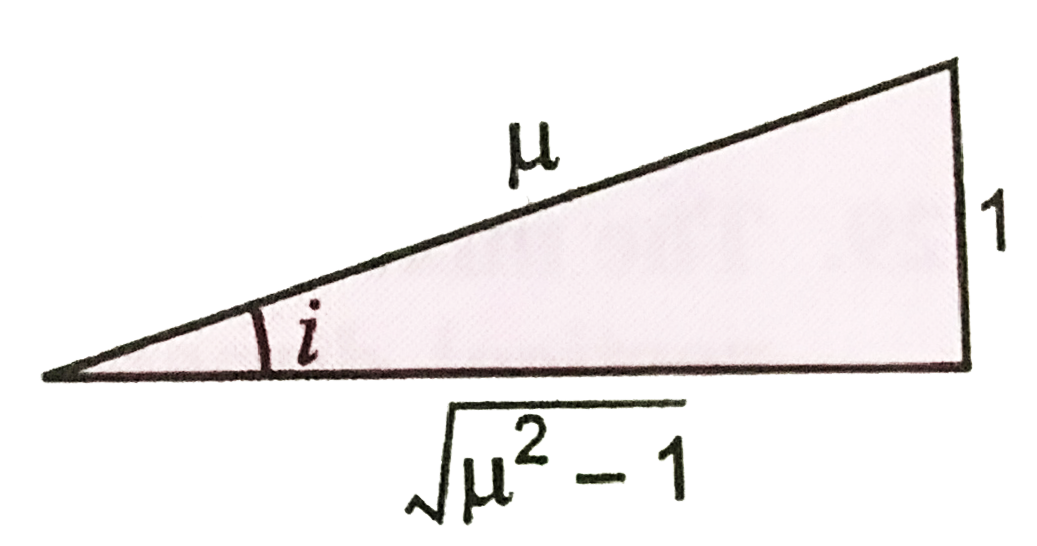
If ,
then ...(i) For total internal reflection, ,
when , Fig. ...(ii)
From (i) and (ii),
Topper's Solved these Questions
- OPTICSBook:PRADEEPChapter:OPTICSExercise:Very short answer question
Explore 5 Videos
- OPTICSBook:PRADEEPChapter:OPTICSExercise:very short answer questions
Explore 1 Video
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Competition Focus (Multiple Choice Questions)
Explore 2 Videos
Similar Questions
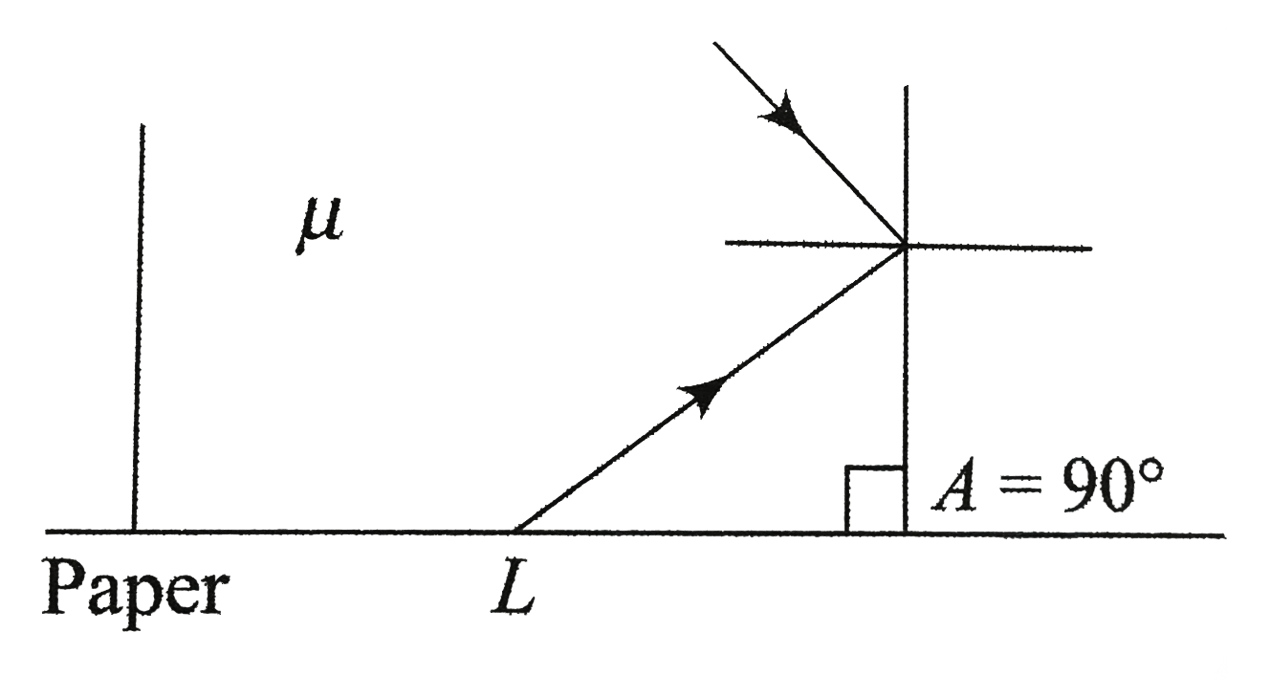
A rectangulat block of refractive index μ is placed on a printed page lying on a horizontal surface as shown in Fig. , Find the minimum value of μ so that the letter L on the page is not visible from any of the vertical sides.
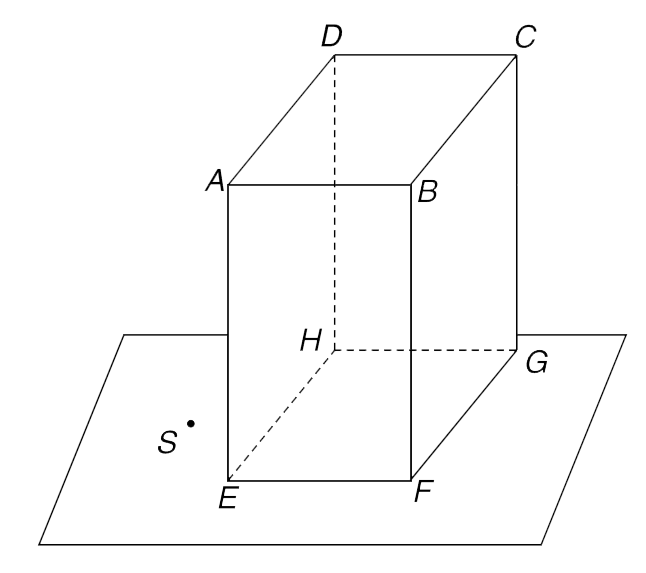
View SolutionA large rectangular glass block of refractive index μ is lying on a horizontal surface as shown in Figure. Find the minimum value of μ so that the spot S on the surface cannot be seen through top plane ‘ABCD’ of the block.
View Solution
Knowledge Check
A small source of light is 4m below the surface of a liquid of refractive index 5/3.In order to cut off all the light comingout of liquid surface,minimum diameter of the disc placed on the surface of liquid is
A3mB4mC6mD∞
A disc is placed on the surface of pond filled with liquid of refractive index 53. A source of light is placed 4m below the surface of liquid. Calculate the minimum area of the disc so that light does not come out of liquid.
View SolutionA jar 15cm long is filled with a transparent liquid. When viewed from the top, its bottom appears to be 12cm below. What is the refractive index of the liquid ?
View SolutionA transparent solid cube of side 'a' has refractive index 3/2. A point source of light is embedded in it at its centre. Find the minimum area of the surface of the cube which must be painted black so that the source is not visible from outside.
View SolutionIn a tank filled with a liquid of refractive index 5/3, a point source of light is placed 2m below the surface of water. To cut off all light coming out of water from the source, what should be the minimum diameter of a disc, which should be placed over the source on the surface of water ?
View SolutionA point source of light S is placed at the bottom of a vessel containg a liquid of refractive index 5/3. A person is viewing the source from above the surface. There is an opaque disc of radius 1cm floating on the surface. The centre of the disc lies vertically above the source S. The liquid from the vessel is gradually drained out through a tap. What is the maximum height of the liquid for which the source cannot at all be seen from above?
View SolutionA fish bowl of diameter 20 cm is filled with a liquid of refractive index 1.4. A letter O is written on the outer surface of the bowl. Determine the position of the image of the word formed when observed through the bowl from the opposite side.
View SolutionA small coin is placed at the bottom of a cylindrical vessel of radius R and height h. If a transparent liquid of refractive index μ completely filled into the cylinder, find the minimum fraction of the area that should be covered in order not to see the coin.
View Solution