A glass of refractive index 1.5 is coated with a thin layer of thickness t and refractive index 1.8 . Light of wavelength λ travelling in air is incident normally on the layer. It is partly reflected at the upper and the lower surfaces of the layer. It is partly reflected at the upper and the lower surfaces of the layer ant the two reflected rays interface . If λ=648nm, obtain the least value of t(in10−8m) which the rays interface constructively.
Here, refractive index of glass plate, μ=1.5, and refractive index of coating layer, μ'=1.8.
When rays of light are reflected from the glass surface and surface of coating layer, the optical path difference between the two rays.
Δx=2μ't, where t is thickness of coating layer.
As μ'>μ, therefore, rays of light suffering reflection from optically denser coating layer undergo a phase change of π or path diff. of λ/2. Therefore, net path difference =Δx'=Δx+λ/2
=2μ't=λ/2
For constructive interference
Δx'=nλ
∴2μ't+λ/2=nλ
2μ't=(n−12)λ
where n=1,2,3...........
The least value of thickness of coating layer corresponding to n=1
∴2μ'tmin=(1−12)λ=λ/2
tmin=λ4μ'
when λ=648nm,μ'=1.8
tmin=6484×1.8=90nm
Topper's Solved these Questions
- OPTICSBOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Very short answer question
5 Videos
- OPTICSBOOK - PRADEEPCHAPTER - OPTICSEXERCISE - very short answer questions
1 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Competition Focus (Multiple Choice Questions)
2 Videos
Similar Questions
A convex lens of focal length 15 cm and a concave mirror of focal length 30 cm are kept with their optic axis PQ and RS parallel but separated in vertical directiion by 0.6 cm as shown . The distance between the lens and mirror is 30 cm . An upright object AB of height 1.2 cm is placed on the optic axis PQ of the lens at a distance of 20 cm from the lens . if A'B' is the image after refraction from the lens and the reflectiion from the mirror , find the distance of A'B' from the pole of the mirror and obtain its magnification . Also locate positions of A' and B' with respect to the optic axis RS.
_E01_247_Q01.png)
View SolutionThe outer surface of a transparent glass slab of refractive index μS=1.5 is coated by a thin layer of transparent medium of refractive index μC=1.6. Orange light of wavelength 6400Å falls normally on the coating. The reflected light at the upper surface and at the lower surface of teh coat interfere destructively. If thickness of the coat is 5K×10−8m, calculate the minimum value of K.
View Solution
Knowledge Check
A wave travelling in air falls on a glass plate . It is partly reflected and partly refracted. What is the phase difference between the reflected and refracted waves ?
A2πBπCπ2DzeroWhite light is incident normally on a glass plate (in air) of thickness 500nm and refractive index of 1.5. The wavelength (in nm) in the visible region (400nm−700nm) that is strongly reflected by the plate is:
A450B600C400D500White light is incident normally on a glass plate (in air) of thickness 500nm and refractive index of 1.5. The wavelength (in nm) in the visible region (400nm−700nm) that is strongly reflected by the plate is:
A450B600C400D500
A ray of light incident from air on a glass plate of refractive index n is partly reflected and partly refracted at the two surfaces of the glass. The displacement y0 in the figure is

View SolutionACB is right-angled glass prism of refractive index 1.5 . ∠A ∠B and ∠C are 60∘ 30∘ and 90∘ respectively.A thin layer of liquid is on the AB. For a ray of light which is incident normally on AC to be totally reflected at AB the refractive index of the liquid on AB should be
View SolutionA ray incident at a point at an angle of incidence of 60∘ enters a glass sphere with refractive index √3 and it is reflected and refracted at the farther surface of the sphere. The angle between the reflected and refracted rays at this surface is:
View SolutionA ray of light incident from air on a glass plate of refractive index n is partly reflected and partly refracted at the two surfaces of the glass. The displacement y0 in the figure is
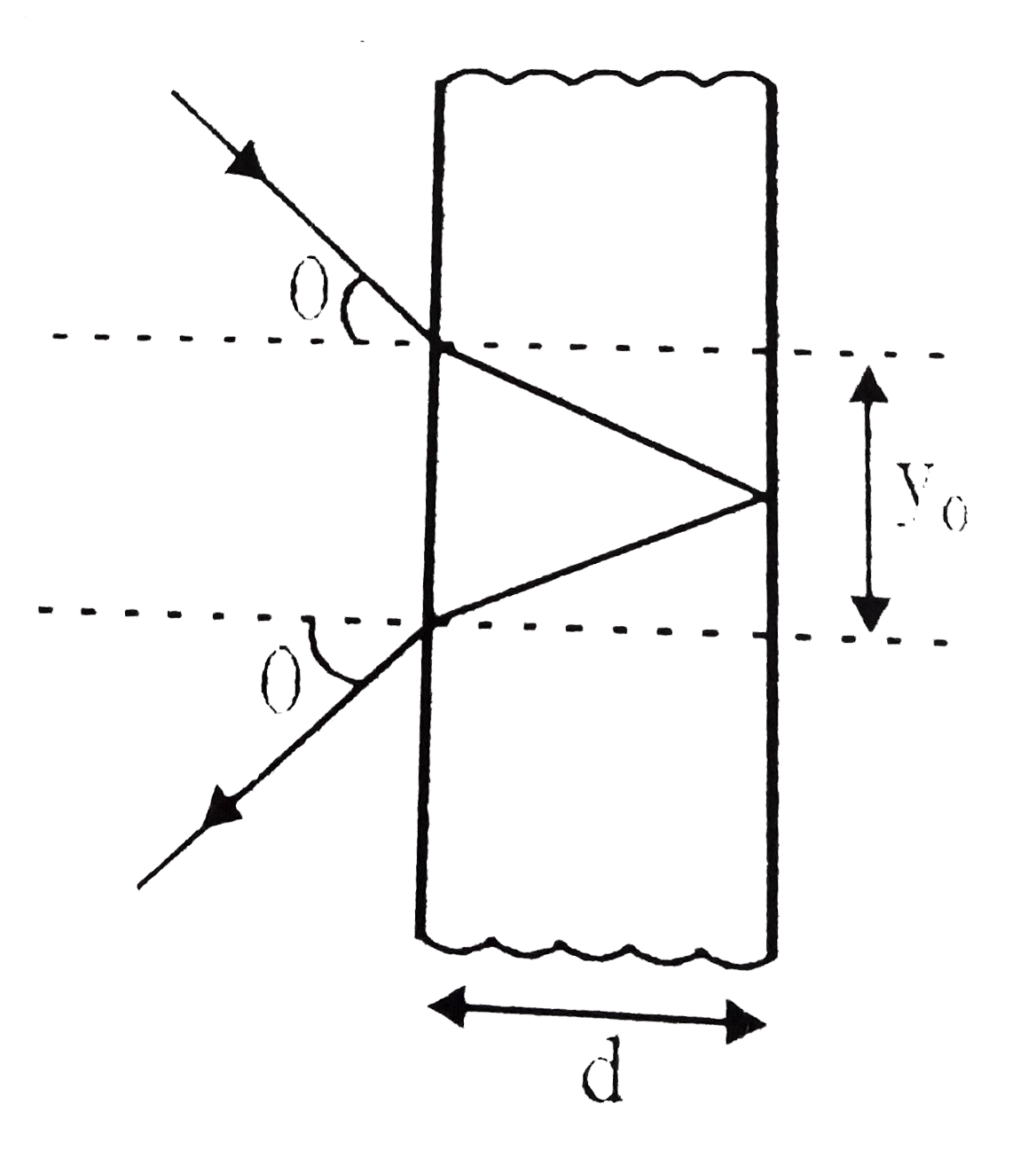
View SolutionPolarising angle for water is 53∘. If light is incident at polarising angle on the surface of water and is partly reflected, the angle of refraction will be
View Solution
