Determine the angular separation between central maximum and first order secondary maximum of the diffraction pattern due to a single slit of width when light of wavelength falls on it normally.
Here,
As is clear from Fig.,
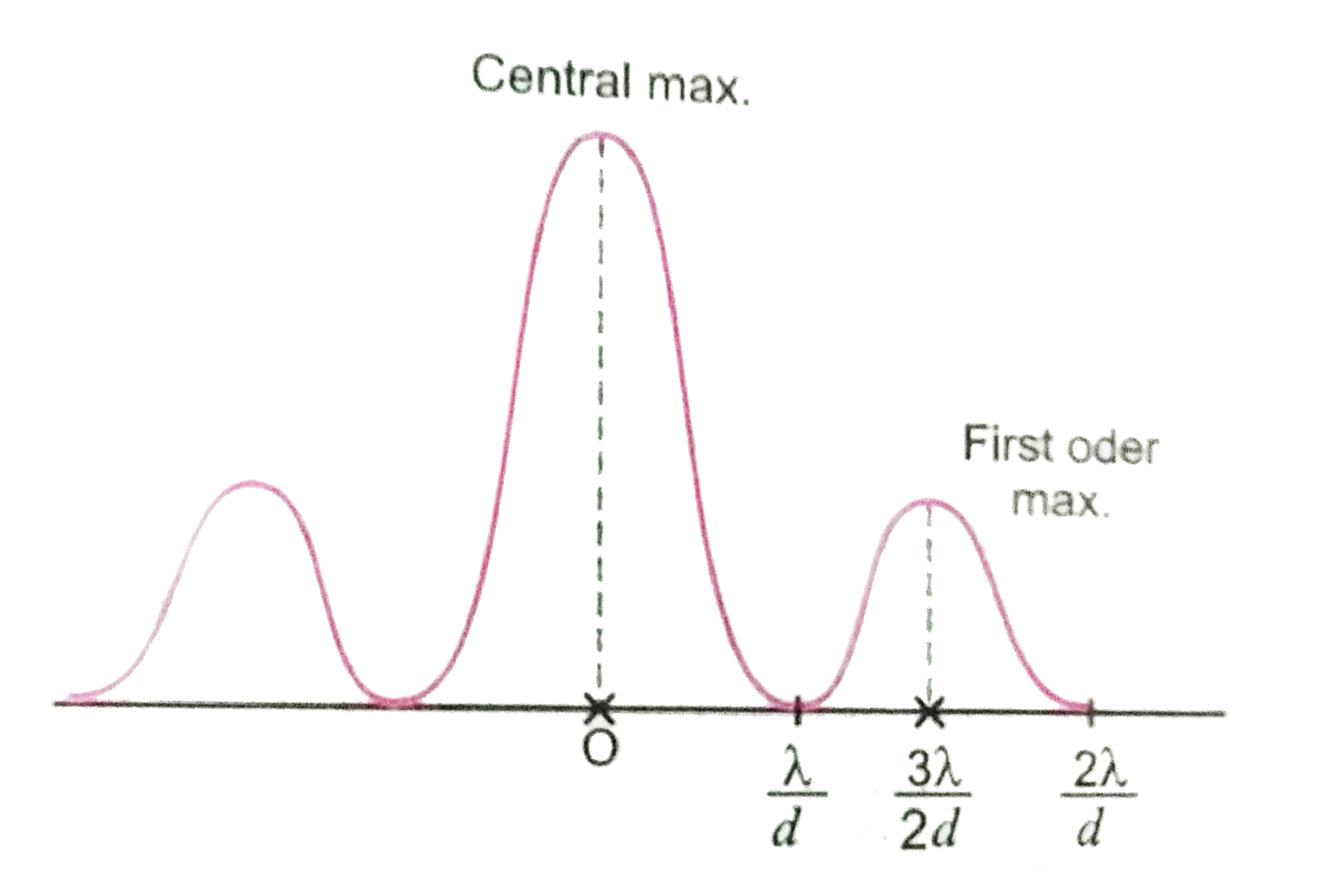
angular separation between central maximum and first order secondary maximum is
Topper's Solved these Questions
- OPTICSBook:PRADEEPChapter:OPTICSExercise:Very short answer question
Explore 5 Videos
- OPTICSBook:PRADEEPChapter:OPTICSExercise:very short answer questions
Explore 1 Video
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Competition Focus (Multiple Choice Questions)
Explore 2 Videos
Similar Questions
Determine the angular spread between central maximum and first order maximum of the diffraction pattern due to a single slit of width 0.25mm, when light of wavelength 5890Å is incident on it normally ?
View Solution(a) Write the factors by which the resolving power of a telescope can be increased.
(b) Estimate the angular separation between first-order maximum and third-order minimum of the diffraction pattern due to a single slit of width 1mm, when light of wavelength 600 nm is incident normal on it.
View Solution
Knowledge Check
What will be the angle of diffraction for the first secondary maximum due to diffraction at a single slit of width 0.5 mm and using light off 5000 Å?
A1.5×10−4 radianB1.5×10−3 radianC0.75×10−3 radianD0.001 radianThe angular width of the central maximum of the diffraction patternn in a single slit (of width a) experiment, with λ as the wavelenth of light, is
A3λ2aBλ2aC2λaDλaAngular width (β) of central maximum of a diffraction pattern on a single slit does not depend upon
A(a) Distance between slit and sourceB(b) Wavelength of the slitC(c) Width of the slitD(d) Frequency of light used
(a) Derive the relation asinθ=λ for the first minimum of the diffraction pattern produced due to a single-slit of width 'a' using light of wavelength λ.
(b) State with reason, how the linear width of central maximum will be affected if (i) monochromatic yellow light is replaced with red light, and (ii) distance between the slit and the screen is increased.
(c) using the monochromatic light of same wavelength in the experimental set-up of the diffraction pattern as well as in the interference pattern where the slit separation is 1mm, 10 interference fringes are found to be within the central maximum of the diffraction pattern. determine the width of the single-slit, if the screen is kept at the same distance from the slit in the two cases.
View Solution(a) Derive the relation a sinθ=λ for the first minimum of the diffraction pattern produced due to a single slit of width ‘a’ using light of wavelengthλ.
(b) State with reason, how the linear width of central maximum will be affected if
(i) monochromatic yellow light is replaced with red light, and
(ii) distance between the slit and the screen is increased.
(c) Using the monochromatic light of same wavelength in the experimental set-up of the diffraction pattern as well as in the interference pattern where the slit separation is 1 mm, 10 interference fringes are found to be within the central maximum of the diffraction pattern. Determine the width of the single slit, if the screen is kept at the same distance from the slit in the two cases.
View SolutionAngular width of central maximum in diffraction at a single slit is……………. .
View SolutionDirection of the first secondary maximum in the Fraunhofer diffraction pattern at a single slit is given by (a is the width of the slit)
View SolutionThe direction of the first secondary maximum in the fraunhoffer diffraction pattern at a single slit is given by (a is the width of the slit)
View Solution

