The ratio of for a travelling wave (where is the angular frequency and k is the angular wave number) is .........
The correct Answer is:speed
To solve the problem of finding the ratio of ωk for a traveling wave, we can follow these steps:
Step 1: Understand the Definitions
- The angular frequency ω is defined as:
ω=2πν
where ν is the frequency of the wave.
- The angular wave number k is defined as:
k=2πλ
where λ is the wavelength of the wave.
Step 2: Write the Ratio
We need to find the ratio ωk:
ωk=2πν2πλ
Step 3: Simplify the Expression
When we simplify the expression, we can multiply by the reciprocal of k:
ωk=2πν⋅λ2π
The 2π terms cancel out:
ωk=νλ
Step 4: Relate to Wave Speed
Now, we know that the wave speed v is given by the product of frequency and wavelength:
v=νλ
Thus, we can conclude:
ωk=v
Final Answer
The ratio ωk for a traveling wave is equal to the speed of the wave v.
---
- The angular frequency ω is defined as:
ω=2πν
where ν is the frequency of the wave.
k=2πλ
where λ is the wavelength of the wave.
We need to find the ratio ωk:
ωk=2πν2πλ
When we simplify the expression, we can multiply by the reciprocal of k:
ωk=2πν⋅λ2π
The 2π terms cancel out:
ωk=νλ
Now, we know that the wave speed v is given by the product of frequency and wavelength:
v=νλ
Thus, we can conclude:
ωk=v
The ratio ωk for a traveling wave is equal to the speed of the wave v.
Topper's Solved these Questions
- ELECTROMAGNETIC WAVESBook:PRADEEPChapter:ELECTROMAGNETIC WAVESExercise:(C) Problems for practice
Explore 1 Video
- ELECTROMAGNETIC WAVESBook:PRADEEPChapter:ELECTROMAGNETIC WAVESExercise:Multiple choice questions
Explore 1 Video
- ELECTROMAGNETIC WAVESBook:PRADEEPChapter:ELECTROMAGNETIC WAVESExercise:Value based questions
Explore 5 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBook:PRADEEPChapter:ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTExercise:Multiple Choice Questions
Explore 1 Video
- ELECTRONIC DEVICESBook:PRADEEPChapter:ELECTRONIC DEVICESExercise:Fill in the Blanks
Explore 1 Video
Similar Questions
Knowledge Check
The angular speed ω is given by
A2πnB2π/TC2π/nDboth 'a' and 'b'The graph between wave number (→v) and angular frequency (ω) is
A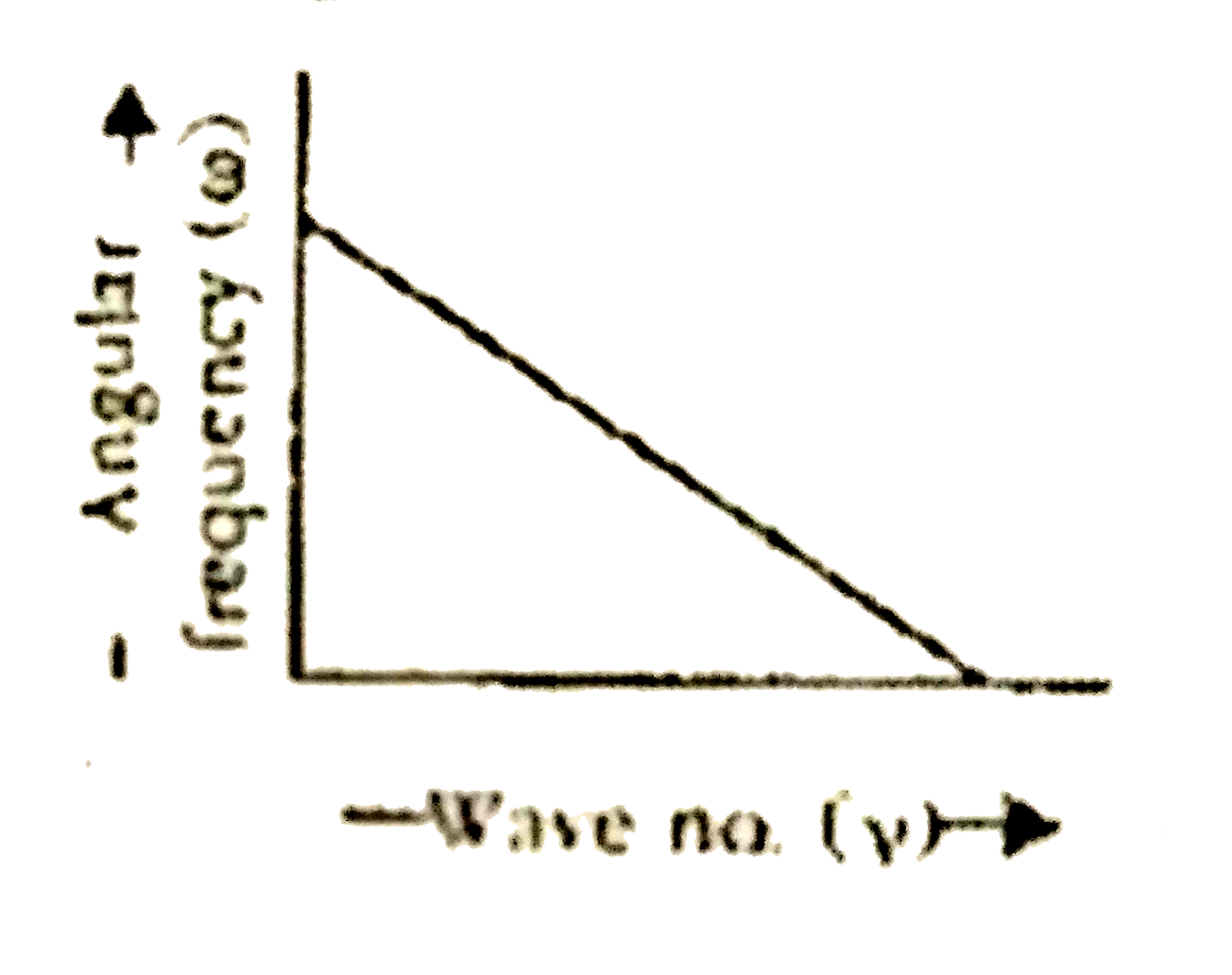 B
B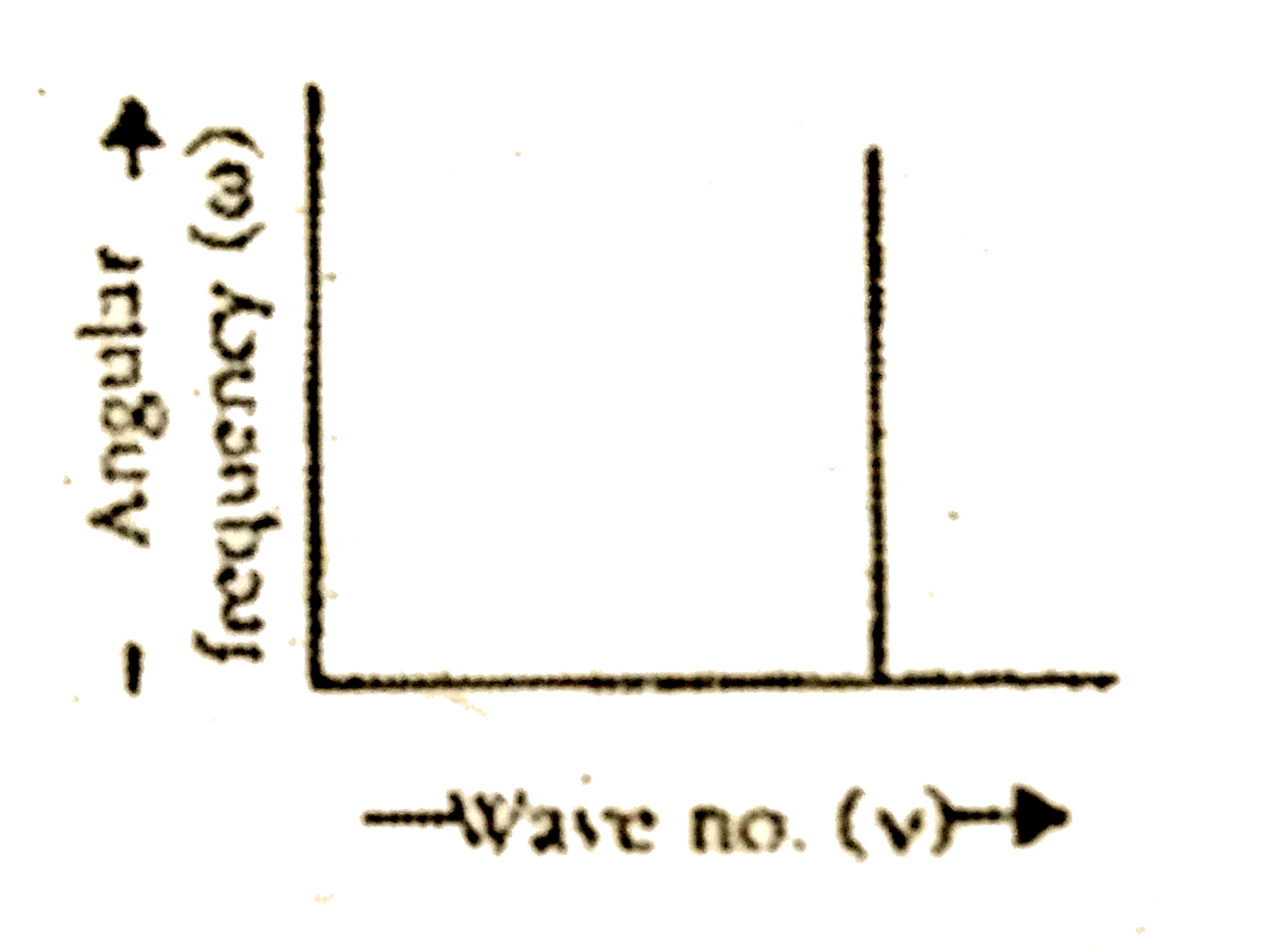 C
C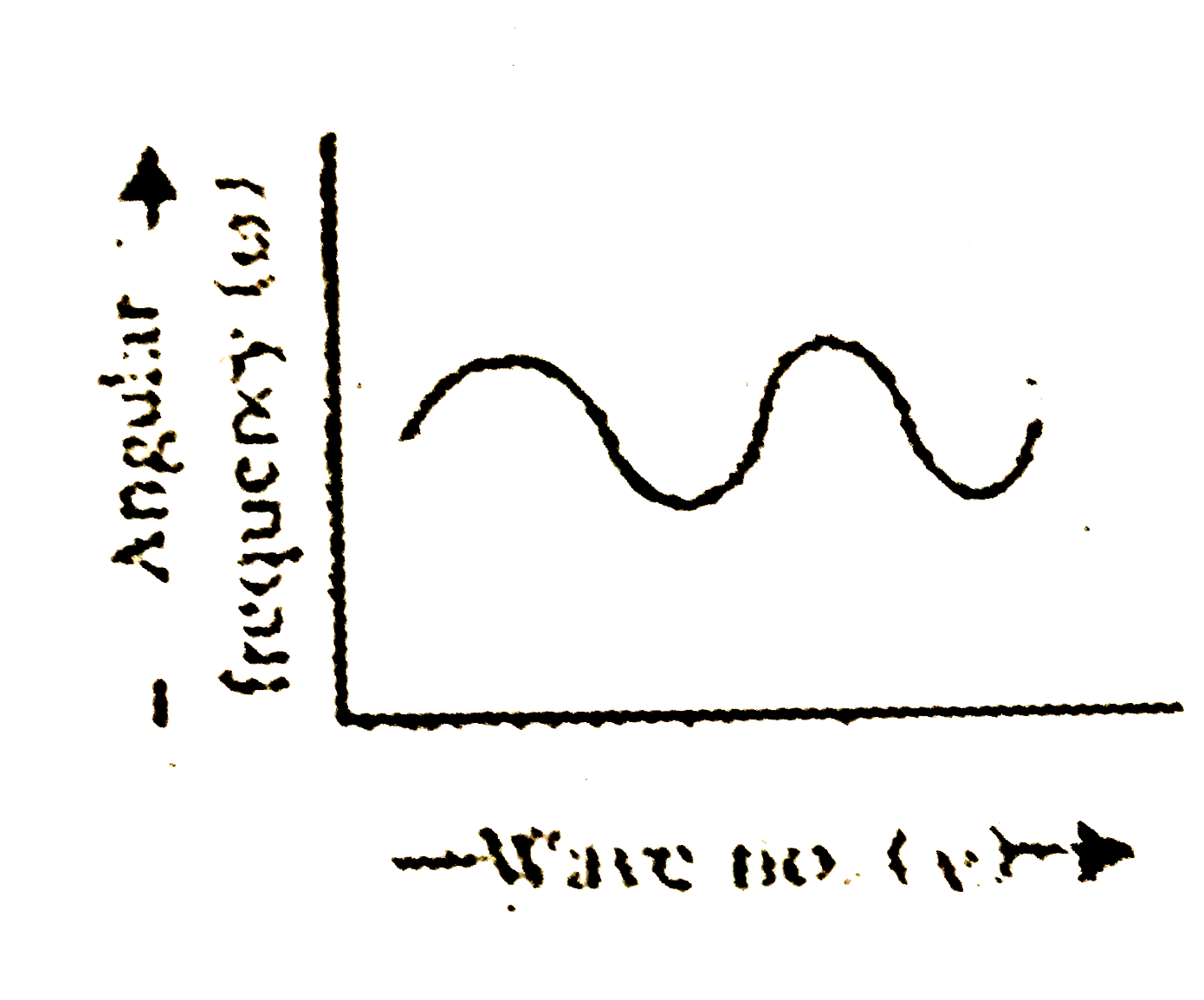 D
D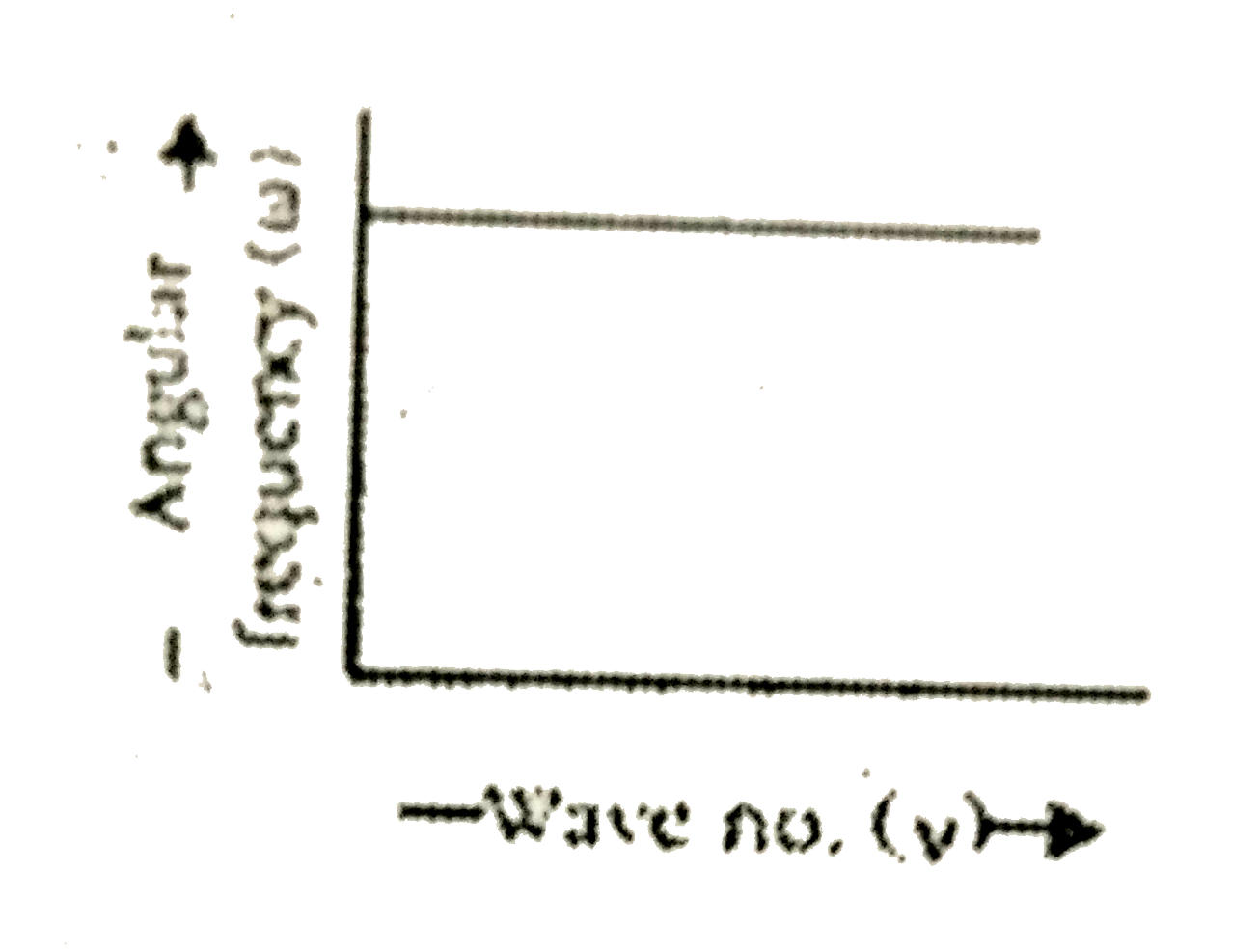
The equation of a wave is given by Y=Asinω(xv−k)
where ω is the angular velocity and v is the linear velocity. The dimension of k isA[LT]B[T]C[T−1]D[T2]
The equation of a wave is given by Y=Asinω(xv−k), where ω is the angular velocity and v is the linear velocity. Find the dimension of k.
View SolutionIf ω0=√k/m, angular frequency in SHM, then k refers to
View SolutionA longitudinal standing wave y=acoskxcosωt is maintained in a homogeneious medium of density ρ. Here ω is the angular speed and k , the wave number and a is the amplitude of the standing wave . This standing wave exists all over a given region of space.
The space density of the kinetic energy . KE=Ek(x,t) at the point (x,t) is given by
View SolutionA longitudinal standing wave y=acoskxcosωt is maintained in a homogeneious medium of density ρ. Here ω is the angular speed and k , the wave number and a is the amplitude of the standing wave . This standing wave exists all over a given region of space.
The space density of the potential energy PE=Ep(x,t) at a point (x,t) in this space is
View SolutionThe angular wave function depends upon quantum numbers.
View Solution

