An inductor , a resistor and a battery are connected in series. Find (a) the time constant, (b) the maximum current and (c ) the time elapsed before the current reaches 99% of the maximum value.
Here, .
Time constant,
Maximum current,
Using
.
Solve to get
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - JEE Mains Ad..(Multiple Choice Question)
1 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Multiple Choice Questions
1 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Value Based Questions
2 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise
191 Videos
- ELECTROMAGNETIC WAVESBOOK - PRADEEPCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - II Focus multiple choice question
5 Videos
Similar Questions
An L-R combination is connected to an ideal battery. If L=20mH,R=100Ω and ε=10V, find (i) the time constant (ii) the maximum current and (iii) the time elapsed before the current reaches 90% of the maximum value.
View SolutionAn inductor (L=20mH), a resistor (R=100Ω) and a battery (verepsilon = 10 V) are connected in series. After along time the circuit is short- circuited and then the battery is disconnected. Find the current in the cirucit 1ms after short- circuititig.
View Solution
Knowledge Check
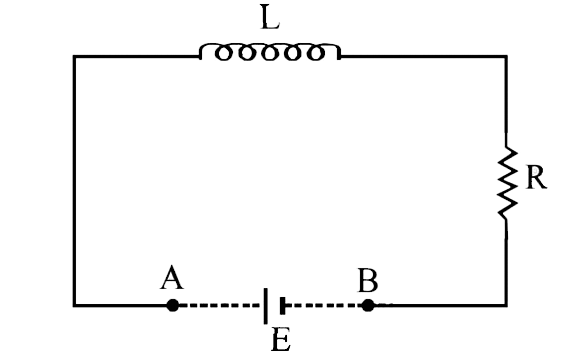
An inductor (L=100mH), a resistor (R=100Ω), and a battery (W=100V) are initially connected in series as shown by the figure. After a long time the battery is disconnected after short circuiting the points A and B. The currents in the circuit 1mm after the short circuit is
 A0.1AB1AC1eADeA
A0.1AB1AC1eADeAAn inductor (L=100mH), a resistor (R=100(Ω)) and a battery (E=100V) are initially connected in series as shown in the figure. After a long time the battery is disconnected after short circuiting the point A and B. The current in the circuit 1 ms after the short circuit is
 A1eABeAC0.1AD1A
A1eABeAC0.1AD1AAn inductor 20mH, a capacitor 100μF and a resistor 50Ω are connected in series across a source of emf, V=10sin314t. The power loss in the circuit is
A2.74WB1.13WC0.43WD0.79W
An inductor (L = 100 mH), a resistor (R=100Ω) and a battery (E = 100 V) are initially connected in series as shown in the figure. After a long time the battery is disconnected after short circuiting the points A and B. The current in the circuit 1 ms after the short circuit is
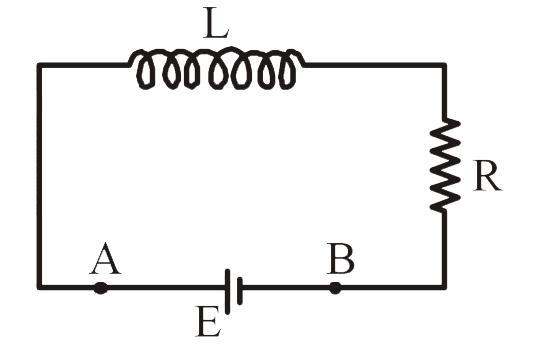
View SolutionHow many time constant will elapse before the power delivrered by the battery drops to half of its maximum value.
View SolutionA solenoid of inductance 50 mH and resistance 10 Omega is connected to a battery of 6V. Find the time elapsed before the current acquires half of its steady - stae value.
View SolutionA 100V battery, a 5.00Vresistor, and a 10.0H inductor are connected in series. After the current in th circuit has reached its maximum value.
View SolutionTwo resistors, one of 10Ω and the other of 20Ω , are conneted in series to a 6 V battery. The current in the circuit will be ____.
View Solution
