A capacitor of 1μF is placed in series with a resistor of 2 mega-ohm and a battery of emf 2 V. Calculate the time after which the charge will grow to 86.74% of its max value.
Here, C=1μF=10−6F,
R=2mega−ohm=2×106Ω,V=2volt
t=?qq0=86.47100
τ=RC=2×106×10−6=2s
From q=q0(1−e−t/τ)
qq0=1−e−t/τ
or e−t/τ=1−qq0=1=86.74100=13.53100
e−t/2=13.53100 or et/2=10013.53
t2=(loge100−loge13.53)
=2.303(2−1.1310)
t=2×2.303(0.8690)=4.0s
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBook:PRADEEPChapter:ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTExercise:JEE Mains Ad..(Multiple Choice Question)
Explore 1 Video
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBook:PRADEEPChapter:ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTExercise:Multiple Choice Questions
Explore 1 Video
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBook:PRADEEPChapter:ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTExercise:Value Based Questions
Explore 2 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:PRADEEPChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Exercise
Explore 191 Videos
- ELECTROMAGNETIC WAVESBook:PRADEEPChapter:ELECTROMAGNETIC WAVESExercise:II Focus multiple choice question
Explore 5 Videos
Similar Questions
A capacitor of 1.0μF is connected to series with a resistance of 104ohm, and a battery of 2.0 V. Find the maximum value of current and current after 0.02 s.
View SolutionA 20 mH coil is connected in series with a 2kΩ resistor and a 12 V battery.
Calcualte
(i) time constant of the circuit,
(ii) time during which current decrys to 10% of its maximum value.
View Solution
Knowledge Check
A capacitor C=100μF is connected to three resistor each of resistance 1kΩ and a battery of emf9V.
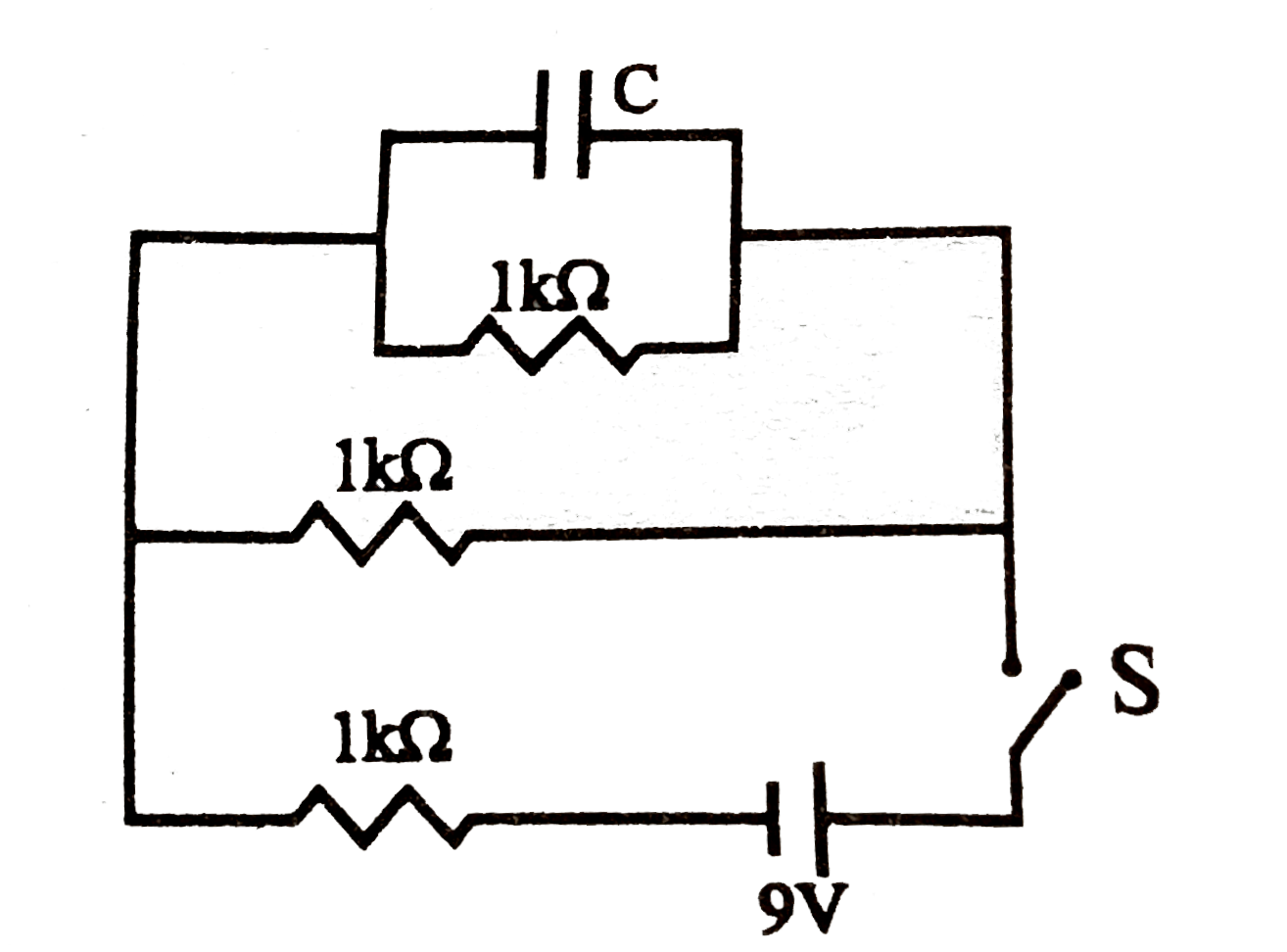
The switch S has been closed for long time so as to charge the capacitor. When switch S is opened, the capacitor discharges with time constantA33msB5msC3.3msD50msA capacitor of capacity 0.1μF connected in series to a resistor of 10MΩ is charged to a certain potential and then made to discharge through resistor. The time in which the potential will take to fall to half its original value is (Given, log102=0.3010)
A2sB0.693sC0.5sD1.0sThree capacitors of 3μF,2μFand6μF are connected in series. When a battery of 10V is connected to then combination then charge on capacitor will be
A5μCB10μCC15μCD20μC
A parallel plate capacitor with circular plates of radius 1m has a capacitor of 1nF. At t=0, it is connected for charging in series with a resistor R=1MΩ across a 2V battery. Calculate the magnetic field at a point P, halfway between the cnetre and the periphery of the plates, after t=10−3sec.
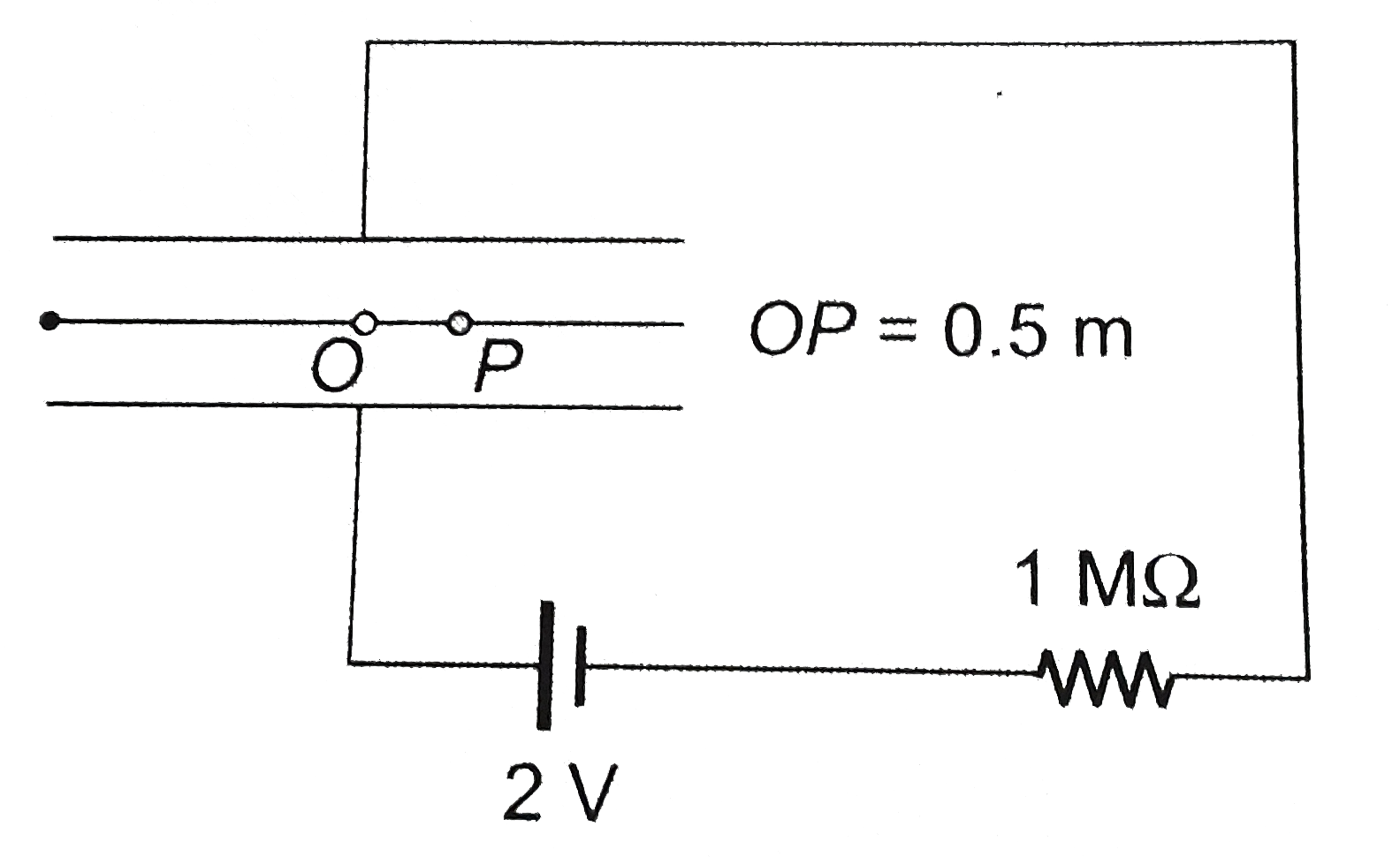
View SolutionA 50 mH inductor is in series with a 10 Ohm resistor and a battery with an emf of 25 V. At t = 0 the switch is closed. Find
Q: How long it takes the current to rise to 90% of its final value?
View SolutionA 3.00MΩ resistor and a 1.00μF capacitor are connected in series with an ideal battery of emf ε=4.00V. At 6.00 s after the connection is made, what is the rate at which (a) the charge of the capacitor is increasing, (b) energy is being stored in the capacitor, (c) thermal energy is appearing in the resistor, and (d) energy is being delivered by the battery?
View SolutionA battery of emf 2 V and internal resistance r is connected in series with a resistor of 10Ω through an ammeter of resistance 2Ω. The ammeter reads 50 mA. Draw the circuit diagram and calculate the value of r.
View SolutionA capacitor of 2μF is conneted to 10 V supply through 1 mega ohm resistance. How long will it take the capacitor to charge upto 63.2% of its final charge ? Also, calculate the maximum value of charge.
View Solution

