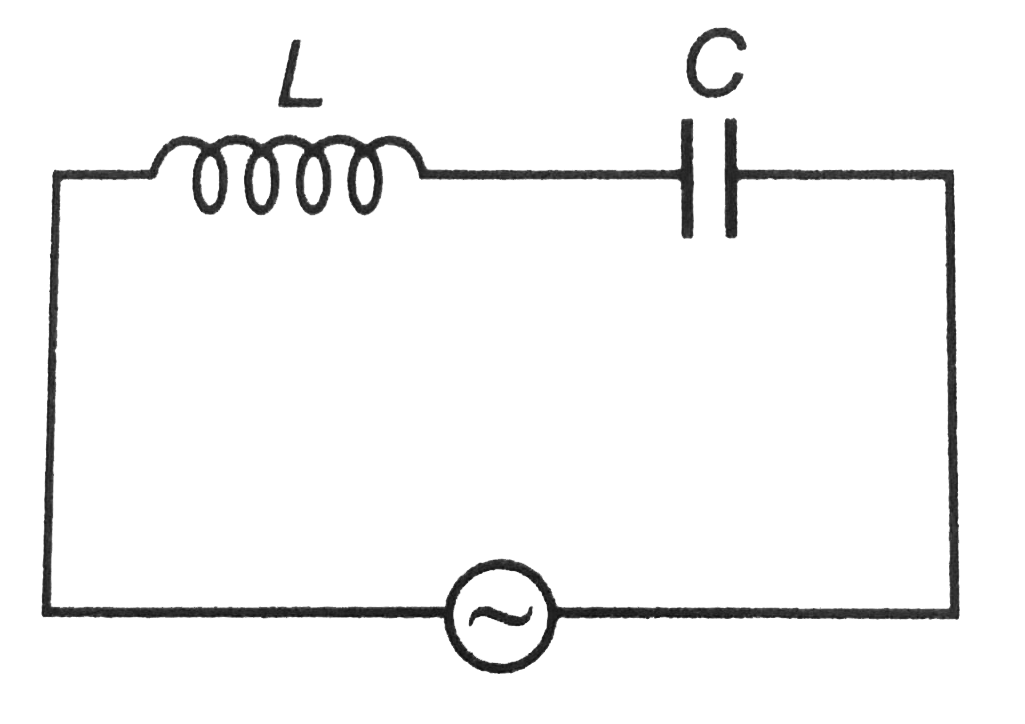
A series LCR circuit is connected to an a.c. source 200 V, 50 Hz. The voltages acorss the resistor, indcutor and capacitor are respectively 200 V, 250 V and 250 V. (i) The algerbriac sum of the three voltages is greater than the source voltage. How is the paradox resolved ?
(ii) If $R = 40 Ω$ , calculate the current in the circuit.

Video Solution

Text Solution

Verified by Experts

Here, $E_{v} = 200 V, v = 52 H z,$
$V_{R} = 200 V, V_{C} = 250 V, V_{L} = 250 V$
Now, $V_{R} + V_{C} + V_{L} = 200 + 250 + 250$
$= 700 V$ , which is greater than the source voltage 200 V. This is because voltages across C and L are in oppsoite phase and canel out. The sum continues to be 200 V, the source voltage.
$I_{v} = \frac{E_{v}}{Z} = \frac{E_{v}}{R} = \frac{200}{40} = A$

Updated on:21/07/2023

An LCR series circuit is connected to an oscillator (AC supply) having RMS voltage 200 V. If the RMS voltages across resistor, inductor and capacitor are equal, then RMS voltage across the resistor would be
A $100 V$
B $\frac{200 V}{\sqrt{2}}$
C $200 V$
D $\frac{100 V}{\sqrt{2}}$
In a series LCR circuit the rms voltage across the inductance , capacitance and resistance are respectively 4 V, 8 V and 5 V . The RMS voltage of the AC source in the circuit is
A17 V
B13 V
C5 V
D6.4 V
A resistance of $200 Ω$ and capacitor of $15 μ F$ are connected in series to a 220 V, 50 Hz AC source. The voltage (rms) across the resistor and capacitor is that
A151 V, 160.4 V
B150 V, 100.3 V
C220 V, 91.8 V
D145 V, 311.3 V