A series LCR circuit is connected to an a.c. source of 220 V - 50 hz. If the readings of voltmeters acorss resistor, capacitor and inductor are 65 V, 415 V and 204 volt respectively , and R=100Ω calculate (i) current in the circuit (ii) value of L (iii) valueo of C and (iv) capacitance required to produce resonance with the given inductor L.
To solve the problem step by step, we will calculate the required values for the series LCR circuit connected to an AC source.
Given Data:
- AC Voltage, Vrms=220V
- Frequency, f=50Hz
- Voltage across Resistor, VR=65V
- Voltage across Capacitor, VC=415V
- Voltage across Inductor, VL=204V
- Resistance, R=100Ω
Step 1: Calculate the Current in the Circuit (Irms)
Using Ohm's law for the resistor:
Irms=VRR
Substituting the values:
Irms=65V100Ω=0.65A
Step 2: Calculate the Inductive Reactance (XL)
Using the voltage across the inductor:
VL=Irms⋅XL
Rearranging gives:
XL=VLIrms
Substituting the values:
XL=204V0.65A≈313.85Ω
Step 3: Calculate the Inductance (L)
The inductive reactance is given by:
XL=ωLwhereω=2πf
Calculating ω:
ω=2π×50≈314.16rad/s
Now substituting for L:
L=XLω=313.85Ω314.16rad/s≈1.000H
Step 4: Calculate the Capacitive Reactance (XC)
Using the voltage across the capacitor:
VC=Irms⋅XC
Rearranging gives:
XC=VCIrms
Substituting the values:
XC=415V0.65A≈638.54Ω
Step 5: Calculate the Capacitance (C)
The capacitive reactance is given by:
XC=1ωC
Rearranging gives:
C=1ωXC
Substituting the values:
C=1314.16rad/s×638.54Ω≈4.99×10−6F≈4.99μF
Step 6: Calculate the Capacitance Required for Resonance (C′)
At resonance, XC=XL:
C′=1ω2L
Substituting the values:
C′=1(314.16rad/s)2×1.000H≈10.1×10−6F≈10.1μF
Summary of Results:
1. Current in the circuit, Irms=0.65A
2. Inductance, L≈1.000H
3. Capacitance, C≈4.99μF
4. Capacitance required for resonance, C′≈10.1μF
- AC Voltage, Vrms=220V
- Frequency, f=50Hz
- Voltage across Resistor, VR=65V
- Voltage across Capacitor, VC=415V
- Voltage across Inductor, VL=204V
- Resistance, R=100Ω
Using Ohm's law for the resistor:
Irms=VRR
Substituting the values:
Irms=65V100Ω=0.65A
Using the voltage across the inductor:
VL=Irms⋅XL
Rearranging gives:
XL=VLIrms
Substituting the values:
XL=204V0.65A≈313.85Ω
The inductive reactance is given by:
XL=ωLwhereω=2πf
Calculating ω:
ω=2π×50≈314.16rad/s
Now substituting for L:
L=XLω=313.85Ω314.16rad/s≈1.000H
Using the voltage across the capacitor:
VC=Irms⋅XC
Rearranging gives:
XC=VCIrms
Substituting the values:
XC=415V0.65A≈638.54Ω
The capacitive reactance is given by:
XC=1ωC
Rearranging gives:
C=1ωXC
Substituting the values:
C=1314.16rad/s×638.54Ω≈4.99×10−6F≈4.99μF
At resonance, XC=XL:
C′=1ω2L
Substituting the values:
C′=1(314.16rad/s)2×1.000H≈10.1×10−6F≈10.1μF
1. Current in the circuit, Irms=0.65A
2. Inductance, L≈1.000H
3. Capacitance, C≈4.99μF
4. Capacitance required for resonance, C′≈10.1μF
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Solved Examples (b)
1 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Short Answer Qusetions
2 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise
191 Videos
- ELECTROMAGNETIC WAVESBOOK - PRADEEPCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - II Focus multiple choice question
5 Videos
Similar Questions
A series LCR circuit is connected to an a.c. source 220 V - 50 Hz as shown in fig. If the reading of the three voltemeters V1,V2,V3 are 65 V, 415 V and 204 V respectively. Calculate (i) current in the circuit (ii) value of inductor L (ii) value of capacitor C (iv) value of C for same L required to produce resonance.
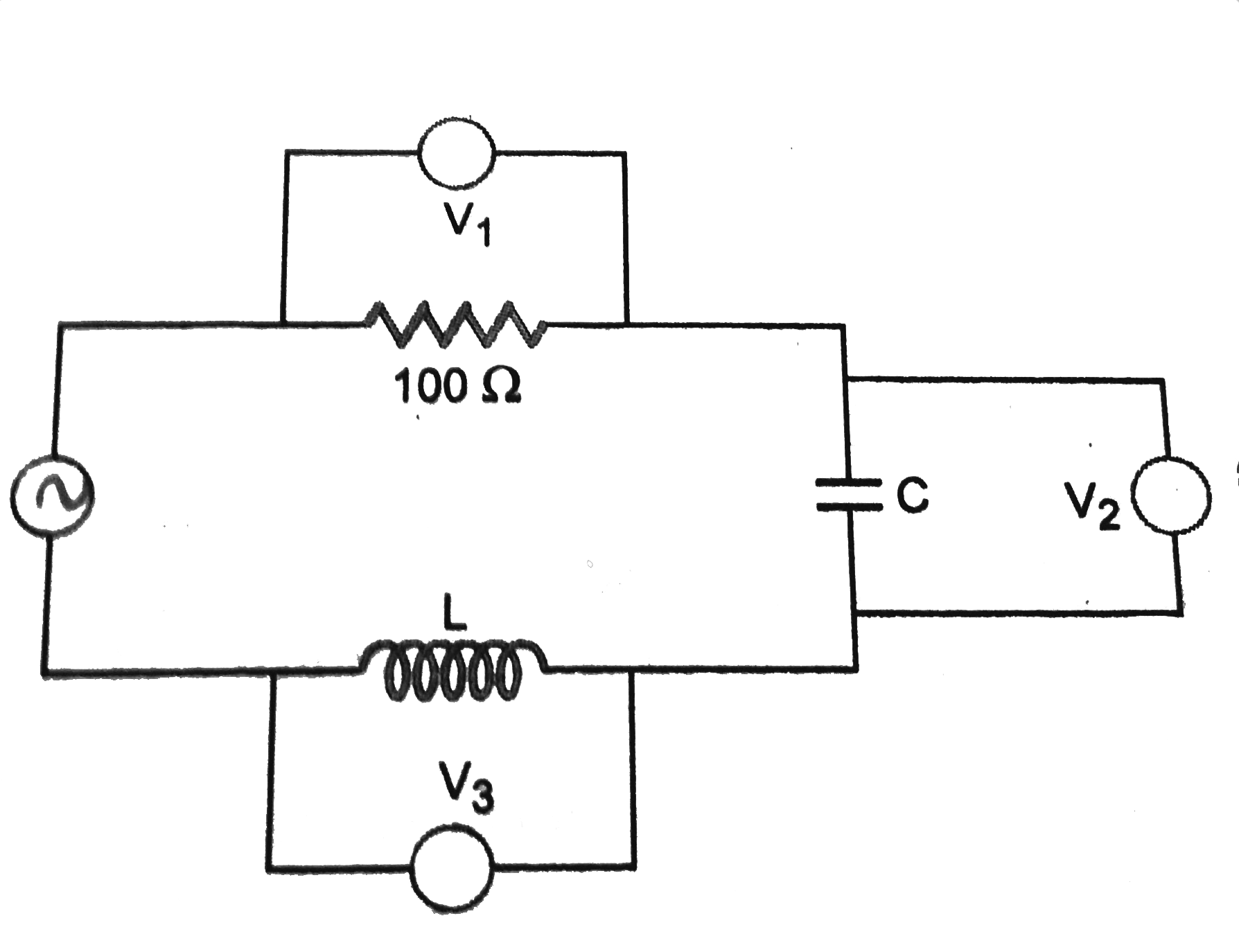
View SolutionIn a series RC circuit connected across an AC source of 220 V 50 Hz calculate the rms voltage across resistor and capacitor if values of R and C are 100 Ω and 20μF respectively .
View Solution
Knowledge Check
In an LCR circuit shown in the following figure, what will be the readings of the voltmeter across the resistor and ammeter if an a.c. Source of 220 V and 100Hz is connected to it as shown?
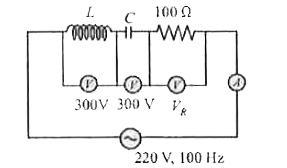 A800V, 8AB110 V, 1.1 AC300 V, 3AD220V, 2.2 A
A800V, 8AB110 V, 1.1 AC300 V, 3AD220V, 2.2 A
A series RLC circuit is connected to an AC supply 220 V, 50 Hz. The value of R is 10 Ω . The value of capacitive reactance of capacitor and incuctive reactance of inductor are 15 Ω and 20Ω respectively . Calculate the value of current in the circuit.
View SolutionA series LCR circuit is connected top an AC power source of 220 V , 50 Hz. The values of L and R are 0.41 H and 80Ω respectively. What is the value of C if current and voltage are in phase ?
View SolutionA 31.4Ω resistor and 0.1H inductor are connected in series to a 200V, 50Hz ac source. Calculate
(i) the current in the circuit
View SolutionAn inductor is connected in series with an capacitor and a resistor to an AC supply of V volts. The readings in voltmeters connected across inductor capacitor and resistor are 120 V, 50 V and 80 V respectively . Calculate the value of V and hence also find the power factor.
View SolutionA series LCR circuit is connected to an a.c. source 200 V, 50 Hz. The voltages acorss the resistor, indcutor and capacitor are respectively 200 V, 250 V and 250 V. (i) The algerbriac sum of the three voltages is greater than the source voltage. How is the paradox resolved ?
(ii) If R=40Ω, calculate the current in the circuit.
View SolutionA 50Ω resistor an inductor and a capacitor are connected to an AC source 220 V. The frequency of source is 50 Hz. Calculate the current in the circuit if voltage across resistor capacitor and inductor is 220 V, 260 V and 260 V, respectively.
View SolutionA 50 Ω resistor is connected in series to an inductor and a capacitor to an AC source 220 V , 50 Hz . Calculate the value of inductance and capacitance if voltages across resistor inductor and capacitor are 75 V , 210 V and 420 V respectively.
View Solution
