The current I ampere is flowing in an equilateral triangle of side a the magnetic field induction at the centroid will be
9μ0I2πa
5√2μ0I3πa
3μ0I2πa
μ0I3√3πa
The correct Answer is:A
To find the magnetic field induction at the centroid of an equilateral triangle with current I flowing through its sides, we can follow these steps:
1. Understand the Geometry:
- We have an equilateral triangle with each side of length a.
- The centroid of the triangle is the point where all three medians intersect.
2. Determine the Position of the Centroid:
- The centroid divides each median in the ratio 2:1. The distance from the centroid to any vertex is 23 of the median length.
- The length of the median m of an equilateral triangle can be calculated using the formula:
m=√32a
- Therefore, the distance R from the centroid to each vertex (which is also the perpendicular distance from the centroid to each side) is:
R=23m=23⋅√32a=√33a
3. Calculate the Magnetic Field Due to One Side:
- The magnetic field B0 at a distance R from a long straight conductor carrying current I is given by:
B0=μ0I2πR
- Substituting R:
B0=μ0I2π(√33a)=3μ0I2π√3a
4. Consider the Contributions from All Three Sides:
- The magnetic field contributions from each side of the triangle at the centroid will have the same magnitude but different directions.
- Using the right-hand rule, we find that the magnetic fields due to each side will add up vectorially.
- The angle between the magnetic field due to one side and the line connecting the centroid to the vertex is 30∘ (since the angles in an equilateral triangle are 60∘).
- Therefore, the total magnetic field B at the centroid is:
B=3B0sin(30∘)=3⋅3μ0I2π√3a⋅12=9μ0I4π√3a
5. Final Result:
- After simplifying, we find:
B=9μ0I2πa
Conclusion:
The magnetic field induction at the centroid of the equilateral triangle is given by:
B=9μ0I2πa
- We have an equilateral triangle with each side of length a.
- The centroid of the triangle is the point where all three medians intersect.
- The centroid divides each median in the ratio 2:1. The distance from the centroid to any vertex is 23 of the median length.
- The length of the median m of an equilateral triangle can be calculated using the formula:
m=√32a
- Therefore, the distance R from the centroid to each vertex (which is also the perpendicular distance from the centroid to each side) is:
R=23m=23⋅√32a=√33a
- The magnetic field B0 at a distance R from a long straight conductor carrying current I is given by:
B0=μ0I2πR
- Substituting R:
B0=μ0I2π(√33a)=3μ0I2π√3a
- The magnetic field contributions from each side of the triangle at the centroid will have the same magnitude but different directions.
- Using the right-hand rule, we find that the magnetic fields due to each side will add up vectorially.
- The angle between the magnetic field due to one side and the line connecting the centroid to the vertex is 30∘ (since the angles in an equilateral triangle are 60∘).
- Therefore, the total magnetic field B at the centroid is:
B=3B0sin(30∘)=3⋅3μ0I2π√3a⋅12=9μ0I4π√3a
- After simplifying, we find:
B=9μ0I2πa
The magnetic field induction at the centroid of the equilateral triangle is given by:
B=9μ0I2πa
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Test Your Grip (a)
Explore 1 Video
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Test Your Grip (c)
Explore 1 Video
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Value Based Questions
Explore 2 Videos
- ELECTROSTATICSBook:PRADEEPChapter:ELECTROSTATICSExercise:ASSERTION-REASON TYPE QUESTIONS
Explore 2 Videos
- OPTICSBook:PRADEEPChapter:OPTICSExercise:Multiple choice questions
Explore 1 Video
Similar Questions
A current of 1A is flowing in the sides of equilateral triangle of side 4.5×10−2m. The magnetic induction at centroid of the triangle:
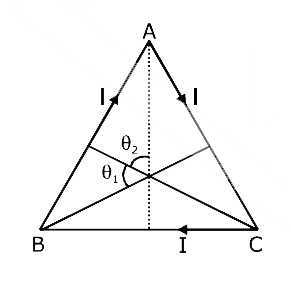
View SolutionA current of 1.0 ampere is flowing in the sides of an equilateral triangle of side 4.5×10−2 m. Find the magnetic field at the centroid of the triangle. (Permeability constant μ0=4π×10−7V−s/A−m)
View Solution
Knowledge Check
A current of 2A is flowing in the sides of an equilateral triangle of side 9 cm. The magnetic field at the centroid of the triangle is
A1.66×10−6TB1.22×10−4TC1.33×10−6TD1.44×10−4TA current I is flowing in a hexgonal coil of side a figure. The magnetic field induction at the centre O of the coil will be
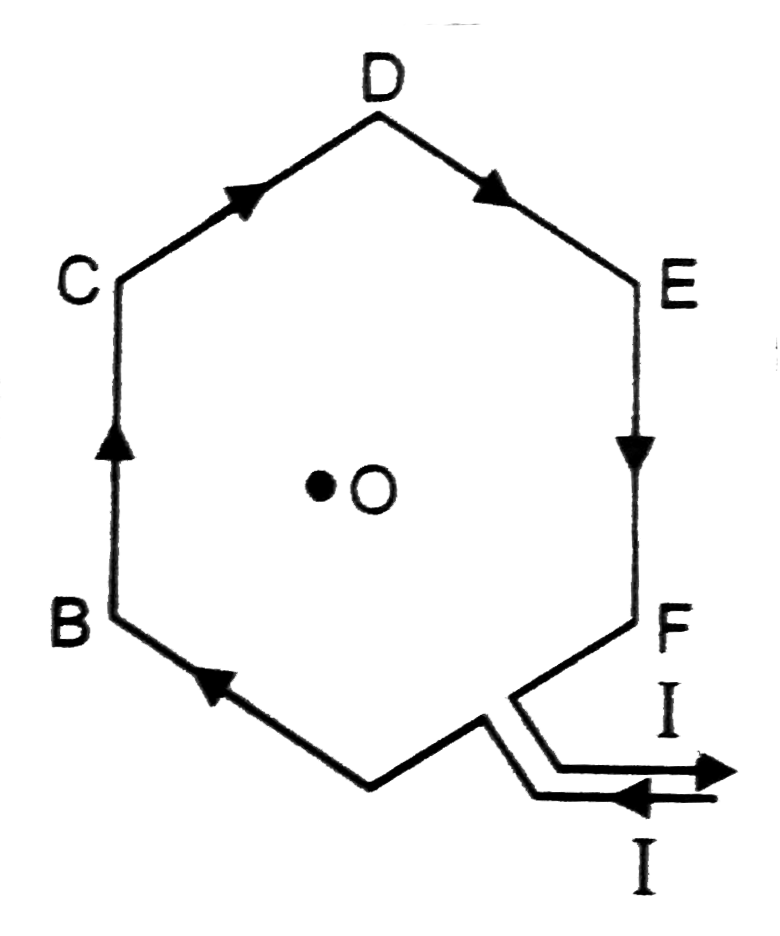 Aμ0I3√3πaB√3μ0IπaC3√3μ0IπaDμ0I√3πa
Aμ0I3√3πaB√3μ0IπaC3√3μ0IπaDμ0I√3πaA current I is flowing in an octagonal coil of side a figure. The magnetic field induction at the centre O of the coil will be
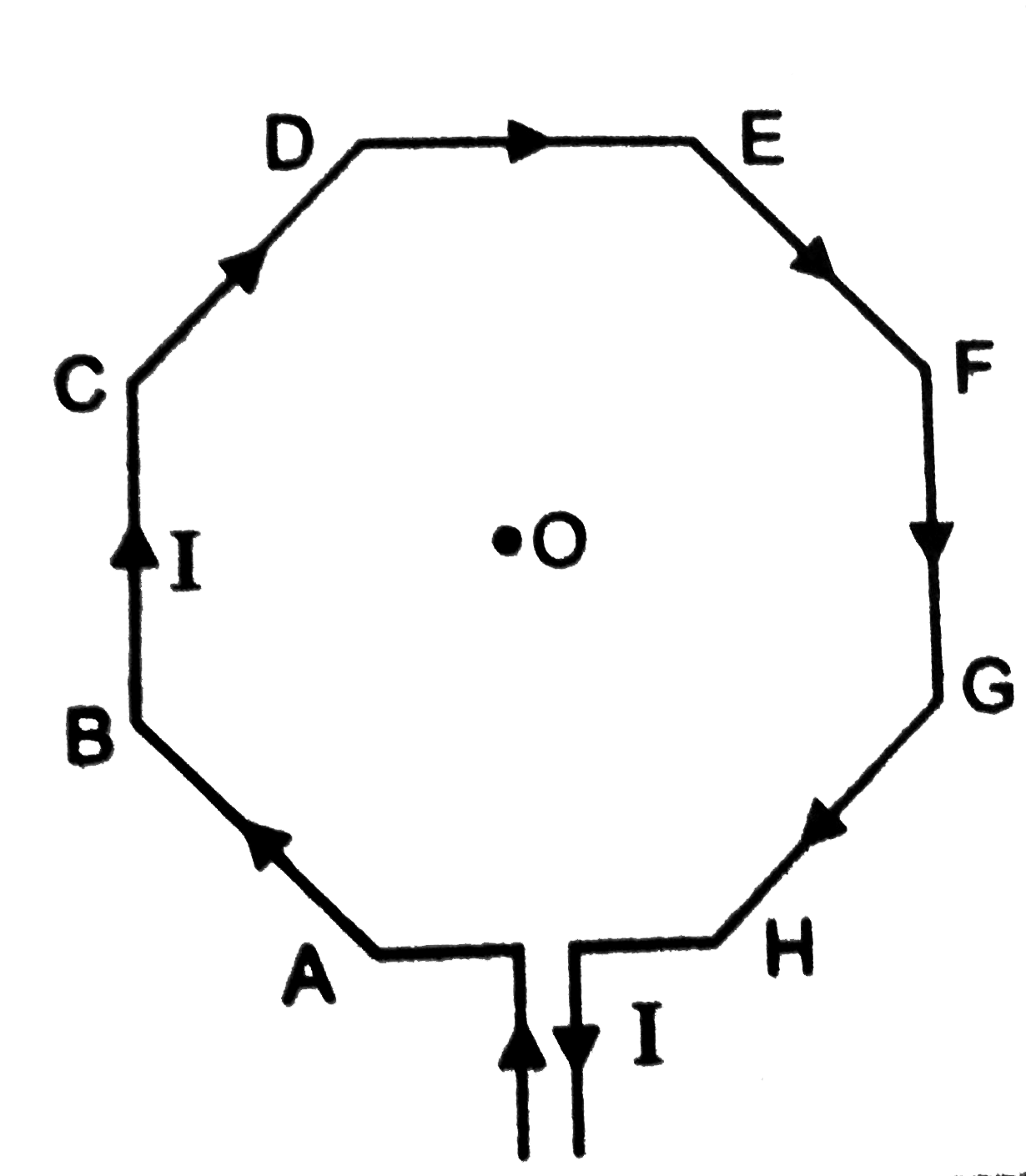 A√5μ0I2πaBμ0I√5πaC5√2μ0IπaD5μ0I4πa
A√5μ0I2πaBμ0I√5πaC5√2μ0IπaD5μ0I4πa
A current of 1⋅0A flowing in the sides of an equilateral triangle of side 4⋅5×10−2m. Find the magnetic fied at the centroid of the triangle.
View SolutionTwo charged particles of charges +0.1 μC and -0.1 μC are kept on the vertices of an equilateral triangle of side 10 cm. Calculate the electric field intensity at the centroid of the triangle.
View SolutionA current of 1.5 A is flowing through a triangle of side 9 cm each .The magnetic field at the centroid of the triangle is : (Assume that the current is flowing in the clockwise direction .)
View SolutionA current I is flowing in a hexgonal coil of side a figure. The magnetic field induction at the centre O of the coil will be

View SolutionA current of 10A is flowing in a equilateral triangle of side length l=1M as shown in figure. The magnetic field at center of triangle is:
_2019_CBT6_E01_040_Q01.png)
View Solution

