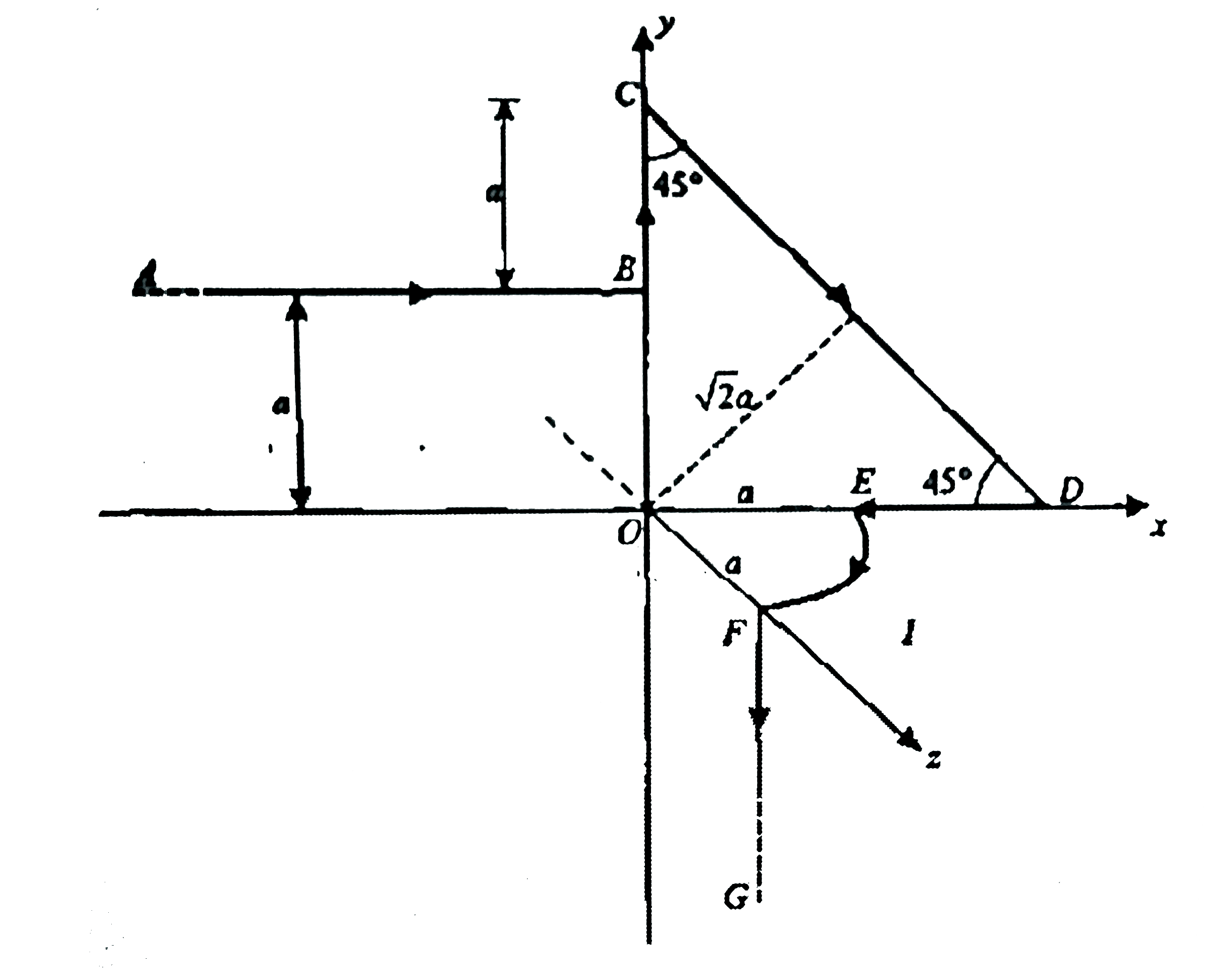
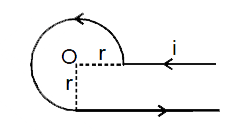
Find the total magnetic induction at point O due to current through curved portion and straight portion in the figure.
Video Solution
Text Solution
B0=BCFE+BCDE , BCFE=μ04πIr(2π−2ϕ)
and BCDE=μ04πIOD[sinϕ+sinϕ]=μ0I×2sinϕ4π×rcosϕ=μ0I4π2tanϕ [∵OD=rcosϕ]
∴B0=μ04πIr(2π−2ϕ)+μ0I4πr×2tanϕ=μ02πr[π−ϕ+tanϕ]
|
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Conceptual Problems (d)
Explore 2 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Very Short Answer Questions (a)
Explore 2 Videos
- ELECTROSTATICSBook:PRADEEPChapter:ELECTROSTATICSExercise:ASSERTION-REASON TYPE QUESTIONS
Explore 2 Videos
- OPTICSBook:PRADEEPChapter:OPTICSExercise:Multiple choice questions
Explore 1 Video
Similar Questions
Knowledge Check
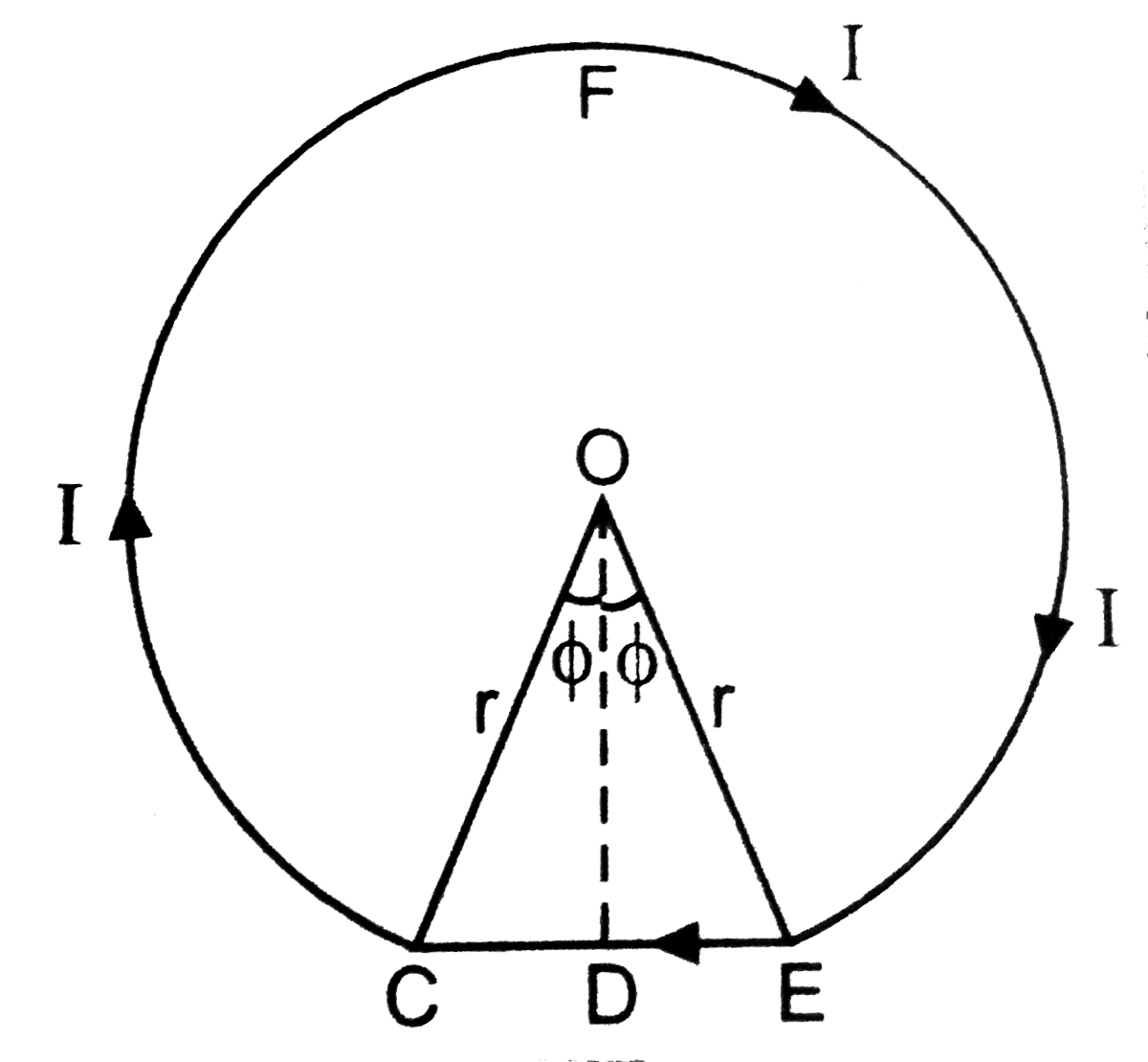
The total magnetic induction at point O due to curve portion and straight portion in the following figure, will be-
 Aμ0i2πr[π−ϕ+tanϕ]Bμ0i2πrC0Dμ0i2πr[π−ϕ+tanϕ]
Aμ0i2πr[π−ϕ+tanϕ]Bμ0i2πrC0Dμ0i2πr[π−ϕ+tanϕ]Find the magnetic induction at point O, if the current carrying wire is in the shape shown in the figure.
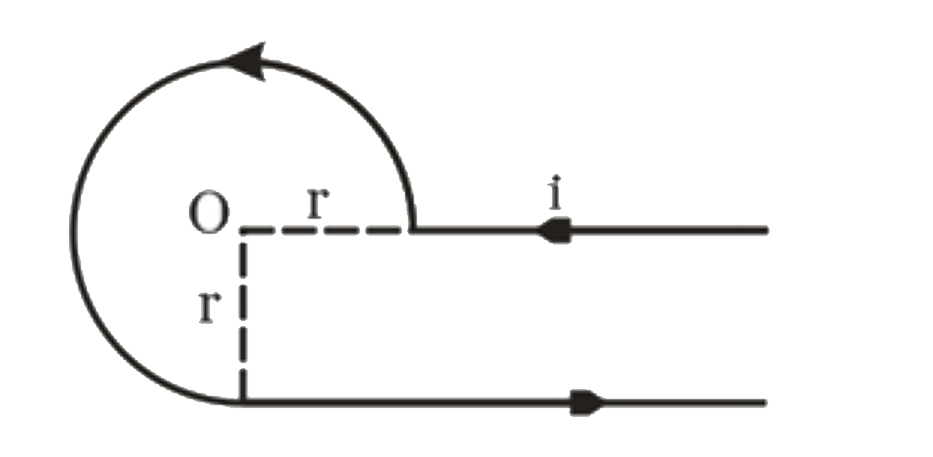 Aμ0l5πr[3π2+1]⊙Bμ0l3πr[3π4+1]⊙Cμ0l2πr[3π4+1]⊙Dμ0l4πr[3π2+1]⊙
Aμ0l5πr[3π2+1]⊙Bμ0l3πr[3π4+1]⊙Cμ0l2πr[3π4+1]⊙Dμ0l4πr[3π2+1]⊙Magnetic induction at the point O in the adjacent figure is
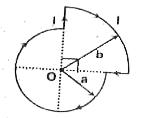 Aμ0i8(3a+1b)Bμ0i4(3a+1b)Cμ0i8π(3a+1b)Dnone of these
Aμ0i8(3a+1b)Bμ0i4(3a+1b)Cμ0i8π(3a+1b)Dnone of these
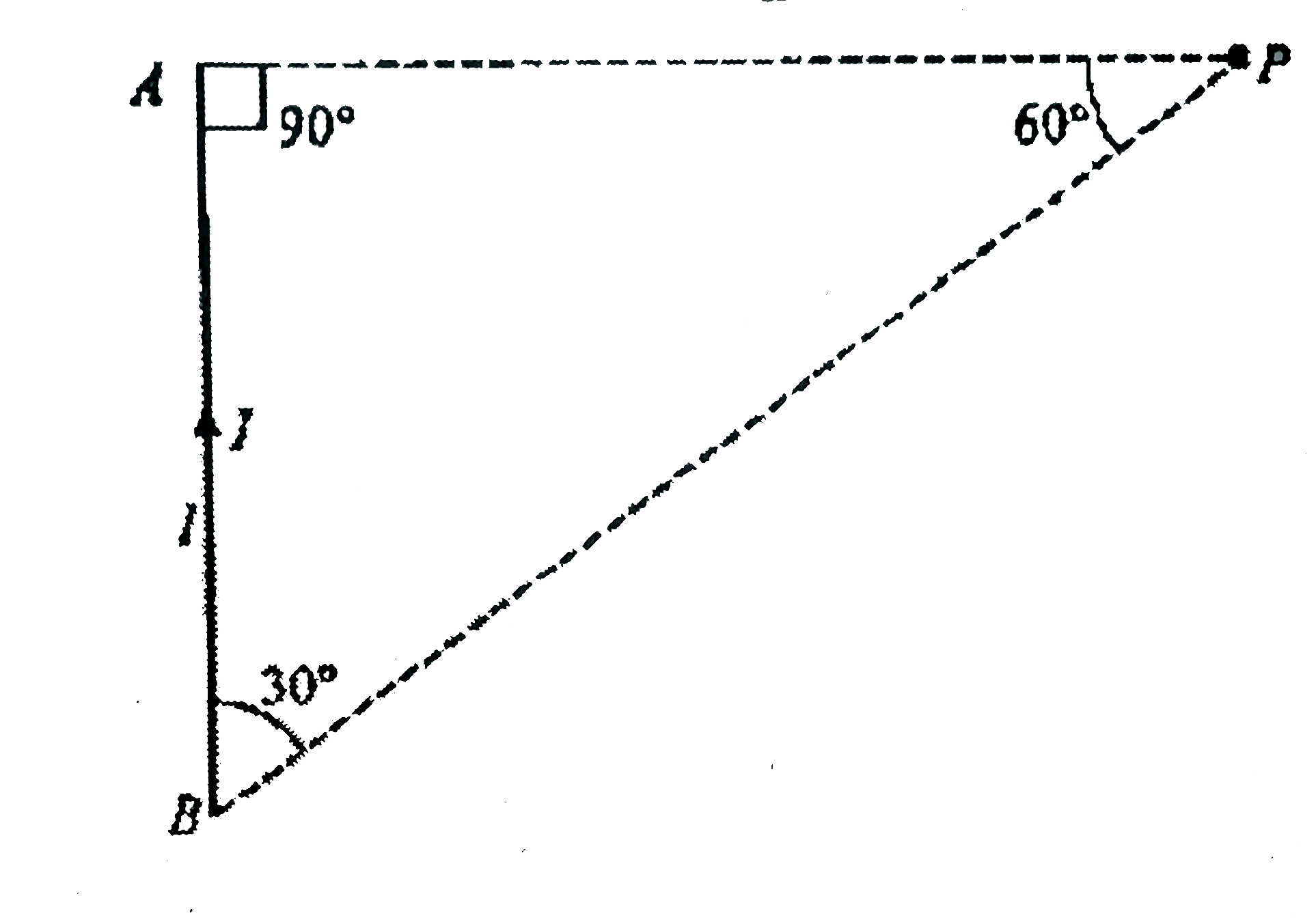
Find the magnetic induction at point P due to a current carrying wire AB as shown in figure-4.31
View SolutionFind the magnetic induction at point O, if the current carrying wire is in the shape shown in the figure
View SolutionMagnetic field at point O due to straight conductor PQ is
_PHY_E06_180_Q01.png)
View SolutionThe magnetic induction at any point due to a long straight wire carrying a current is
View SolutionThe magnetic induction at O due to a current in conductor shaped as shown in figure

View Solution


 .
.