Verify the Ampere's law for magnetic field of a point dipole moment $\to M = M ˆ k$ . Take C as the closed curve running clockwise along (i) z-axis from $z = a > 0$ to $z = R$ , (ii) along the quarter circle of radius R and centre at the origin, in the first quadrant of x-z plane, (iii) along the x-axis from $x = R$ to $x = a$ , and (iv) along the quarter circle of radius a and centre at the origin in the first quadrant of x-y plane.

Video Solution

Text Solution

Verified by Experts

From P to Q, every point on the z-axis lies at the axial line of magnetic dipole of moment $\to M$ . Magnetic field induction at a point distance z from the magnetic dipole of moment $\to M (= M ˆ k)$ is
$∣ ∣ \to B ∣ ∣ = \frac{μ_{0}}{4 π} \frac{2 ∣ ∣ \to M ∣ ∣}{z^{3}} = \frac{μ_{0} M}{2 π z^{3}}$

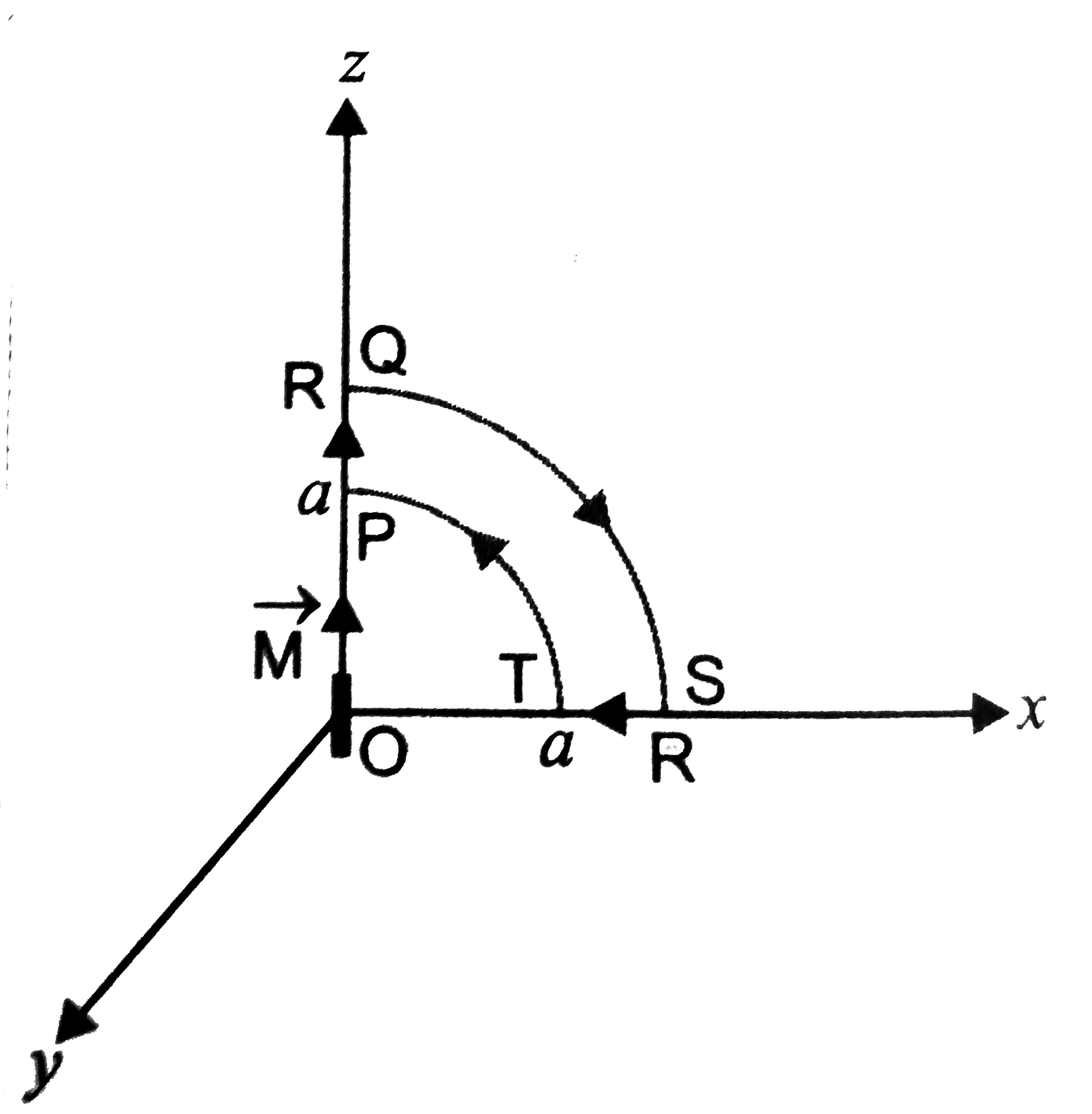
(i) Along z-axis from P to Q.
$\int_{P}^{Q} \to B . d \to l = \int_{P}^{Q} B d l {cos 0}^{\circ} = \int_{a}^{R} B d z$
$= \int_{a}^{R} \frac{μ_{0}}{2 π} \frac{M}{z^{3}} d z = \frac{μ_{0} M}{2 π} (- \frac{1}{2}) (\frac{1}{R^{2}} - \frac{1}{a^{2}}) = \frac{μ_{0} M}{4 π} (\frac{1}{a^{2}} - \frac{1}{R^{2}})$
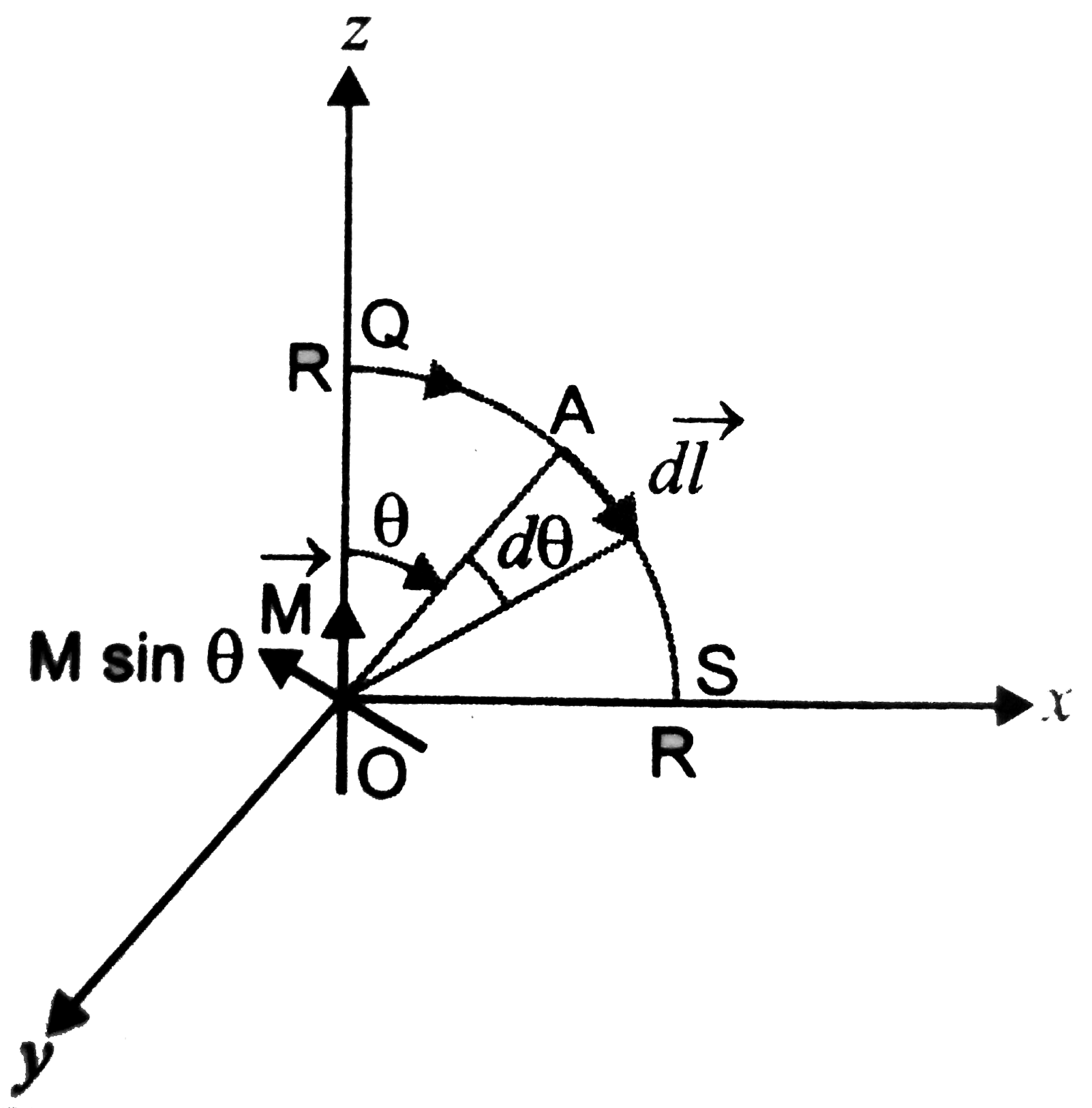
(ii) Along the quarter circle QS of radius R. point A lies on the equatorial line of the magnetic dipole of moment $M sin θ$
Magnetic field at point A on the circular arc is
$B = \frac{μ_{0}}{4 π} \frac{M sin θ}{R^{3}}, d l = R d θ$
$∴ \int_{circular arc Q S} \to B . d \to l = \int B d l cos 0 = \int_{0}^{π / 2} \frac{μ_{0}}{4 π} \frac{M sin θ}{R^{3}} R d θ$
$= \frac{μ_{0}}{4 π} \frac{M}{R^{2}} {(- cos θ)}_{0}^{π / 2} = \frac{μ_{0}}{4 π} \frac{M}{R^{2}}$

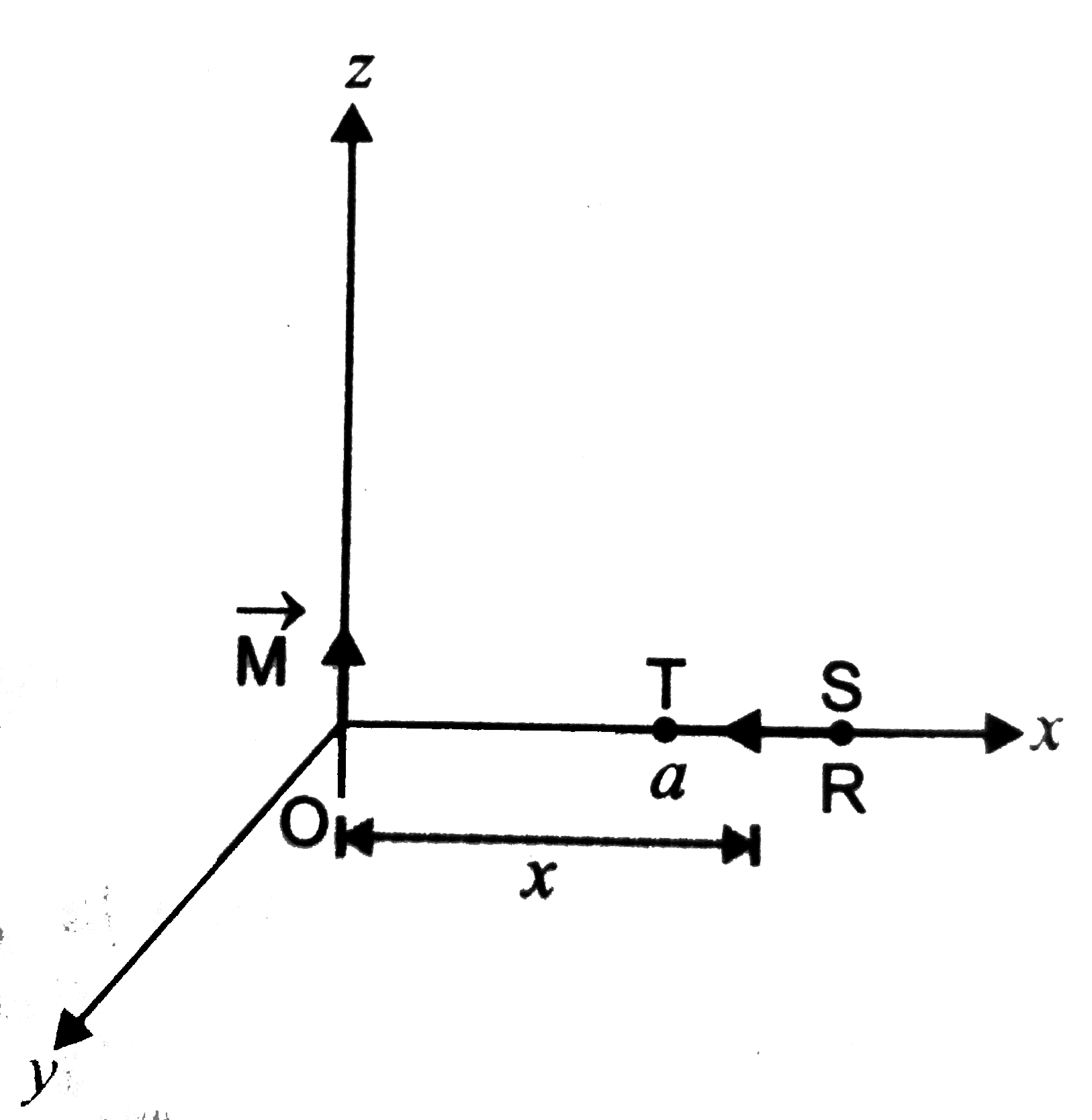
(iii) Along x-axis over the path ST. every point lies on the equatorial line of magnetic dipole. Magnetic field induction at a point distance x from the dipole is
$\to B = - \frac{μ_{0}}{4 π} \frac{\to M}{x^{3}}$
$∴ \int_{S}^{T} \to B . d \to l = \int_{R}^{a} - \frac{μ_{0} \to M}{4 π x^{3}} . d \to l = 0$
$[∵$ angle between $(- \to M)$ and $d \to l$ is $90^{\circ}$ ]

(iv) Along the quarter circle TP of radius a. (ii) Line integral of $\to B$ along the quarter circle TP of radius a is
$\int_{circular arc T P} \to B . d \to l = \int_{π / 2}^{0} \frac{μ_{0}}{4 π} \frac{M sin θ}{a^{3}} a d θ = \frac{μ_{0}}{4 π} (\frac{M}{a^{2}}) \int_{π / 2}^{0} sin t h η d θ$
$= \frac{μ_{0}}{4 π} \frac{M}{a^{2}} {[- cos θ]}_{π / 2}^{0} = - \frac{μ_{0}}{4 π} \frac{M}{a^{2}}$
$∴ \oint_{P Q S T} \to B . d \to l = \int_{P}^{Q} e c B . d \to l + \int_{Q}^{S} \to B . d \to l + \int_{S}^{T} t \to B . d \to l + \int_{T}^{P} \to B . d \to l$
$= \frac{μ_{0} M}{4 π} [\frac{1}{a^{2}} - \frac{1}{R^{2}}] + \frac{μ_{0}}{4 π} \frac{M}{R^{2}} + 0 + (- \frac{μ_{0}}{4 π} \frac{M}{a^{2}}) = 0$

Updated on:21/07/2023