A bar magnetic with poles $25 c m$ apart and pole strength $14 \cdot 4 A . m$ rests with its centre on a frictionless pivot. It is held in equilibrium at $60^{\circ}$ to a uniform magnetic field of induction $0 \cdot 25 T$ by applying a force F at right angles to its axis, $10 c m$ from the pivot. Calculate the value of F. What will happen if the force is removed?

Video Solution

Text Solution

Verified by Experts

Here, $2 l = 25 c m = 25 \times 10^{- 2} m$
$m = 14.4 A m, θ = 60^{\circ}$
$B = 0 \cdot 25 T, r = 10 c m = 0 \cdot 1 m$ , $F = ?$
In equilibrium, torque on the magnet due to magnetic field B is balanced by torque due to external force F applied at $r = 0 \cdot 1 m$ from the centre O.
i.e., $\to M \times \to B = \to r \times \to F$
$M B sin θ = r F {sin 90}^{\circ}$
$F = \frac{M B sin θ}{r} = \frac{(m \times 2 l) B sin θ}{r}$
$= \frac{14.4 \times 25 \times 10^{- 2} \times 0 \cdot 25 {sin 60}^{\circ}}{0 \cdot 1}$
$= \frac{14.4 \times 6.25}{0 \cdot 1} \frac{\sqrt{3}}{2} \times 10^{- 2} = 7 \cdot 794 N$

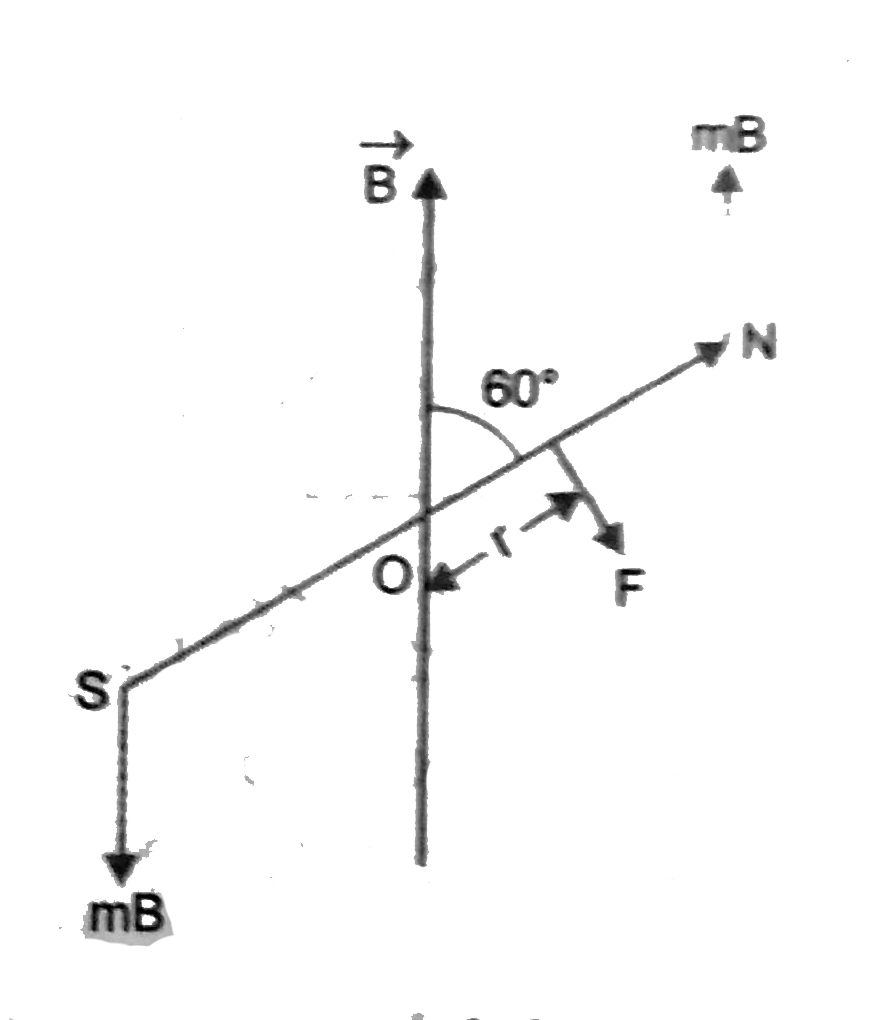
If force $\to F$ is removed, the torque $\to M \times \to B$ will become unbalnced. The magnet will execute oscillatory motion about the direction of $\to B$ , on its pivot O. Further, as $sin θ \neq θ$ , therefore oscillations of the magnet will not be simple harmonic.

Updated on:21/07/2023