Two straight parallel conductors are 50cm apart and carry oppositively directed currents, held perpendicular to the plane of paper as shown in figure. The current in first conductor, I1=20A and in the second conductor is I2=24A. A point P is separated from the first conductor by a distance of 40cm and the second conductor by 30cm. Calculate the magnetic field at point P.
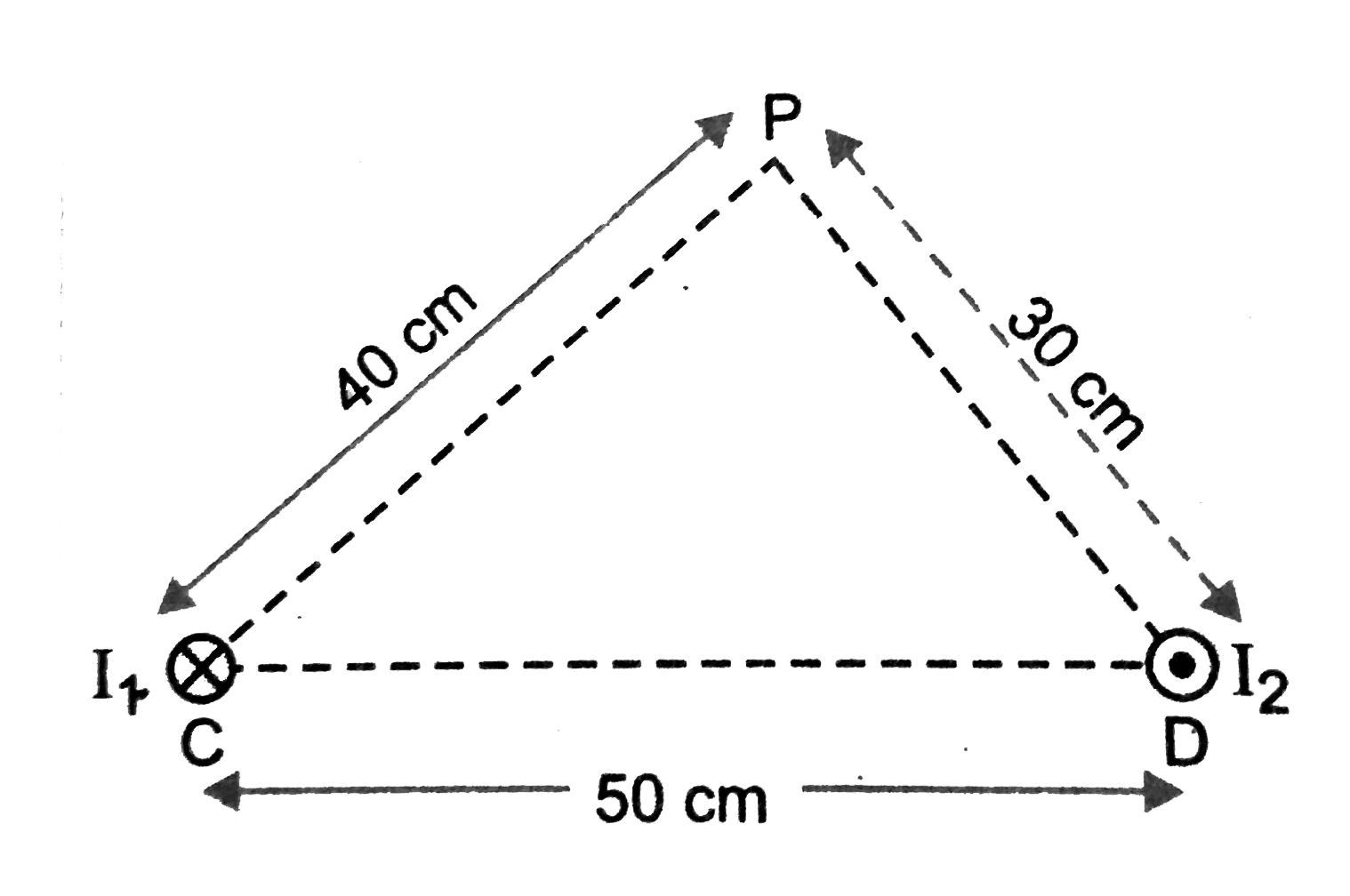
In, figure, CD=50cm, CP=40cm and DP=30cm
As CD2=CP2+DP2
i.e., 50∘=40∘+30∘, so ∠CPD=90∘
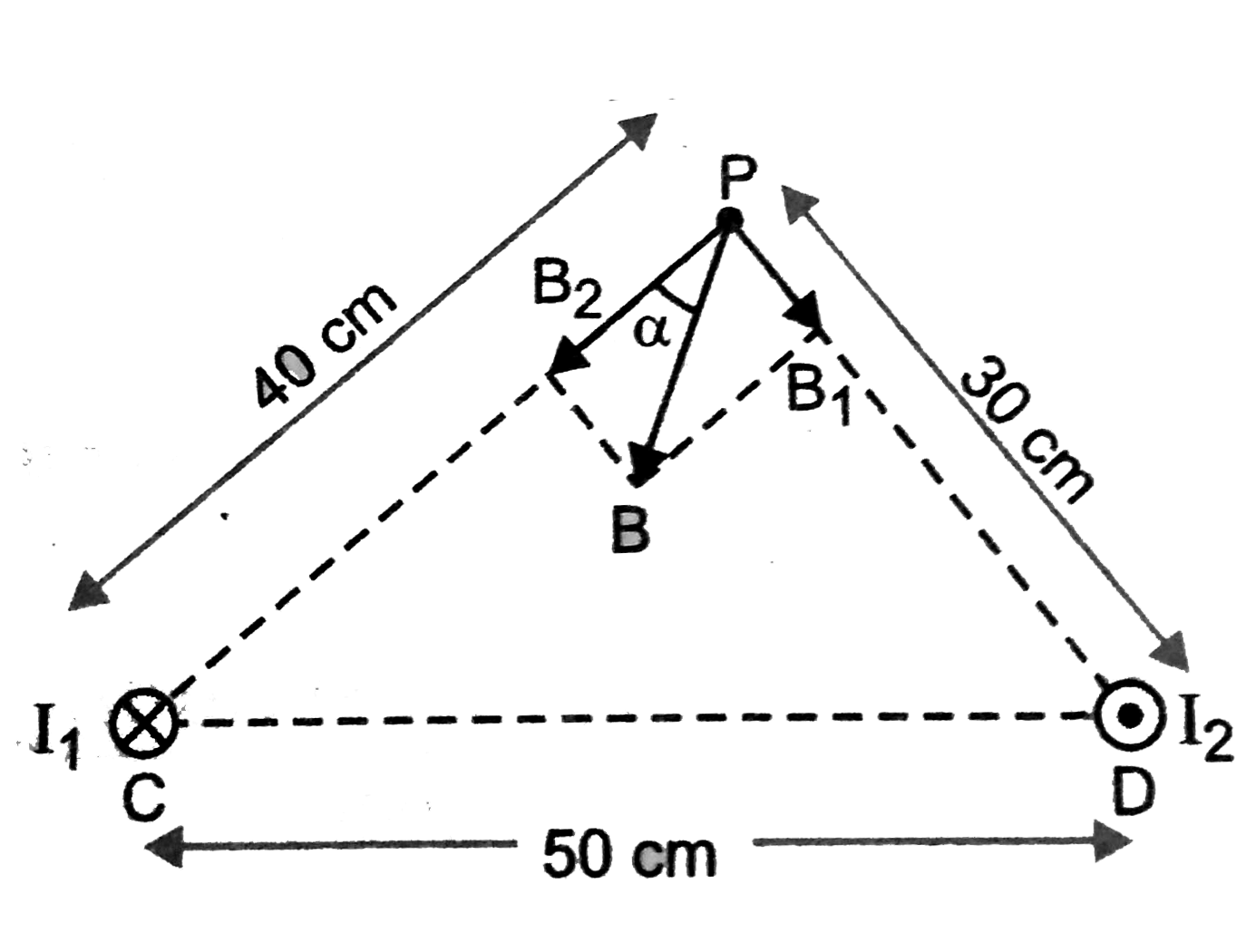
Magnetic field induction at P due to downward current I1 through wire C will be
B1=μ04π2I1r1=10−7×2×200⋅40
=10−5T along P.D.
Magnetic field induction at P due to upward current I2 through wire at D will be
B2=μ04π2I2r2=10−7×2×240⋅30
=1⋅6×10−5T along P.C.
Resultant magnetic field induction at P
B=√B21+B22=√(10−5)2+(1⋅6×10−5)2
=1⋅89×10−5T
Let α be the angle which the resultant magnetic field induction →B make with the direction of →B2, i.e., ∠BPC=α. Then
tanα=B1B2=10−51⋅6×10−5=1016=0⋅625=tan32∘
∴α=32∘, with the line joining the point P with the first conductor.
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Conceptual Problems (d)
2 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Very Short Answer Questions (a)
2 Videos
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - ASSERTION-REASON TYPE QUESTIONS
2 Videos
- OPTICSBOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Multiple choice questions
1 Video
Similar Questions
Knowledge Check
Shown in the figure is a conductor carrying a current i. the magnetic field at the origin is :
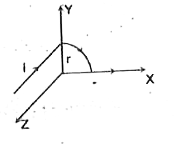 Aμ0i4r(ˆiπ+ˆj2)B−μ0i4r(ˆiπ+ˆk2)Cμ0i4r(ˆi2+ˆiπ)Dμ0i4r(2ˆiπ+ˆj)
Aμ0i4r(ˆiπ+ˆj2)B−μ0i4r(ˆiπ+ˆk2)Cμ0i4r(ˆi2+ˆiπ)Dμ0i4r(2ˆiπ+ˆj)The magnetic field at a perpendicular distance of 2cm from an infinite straight current carrying conductor is 2×10−6T. The current in the wire is
A0⋅1AB0⋅2AC0⋅4AD0⋅8AAB and CD are long straight conductor, distance d apart, carrying a current I. The magnetic field at the midpoint of BC is
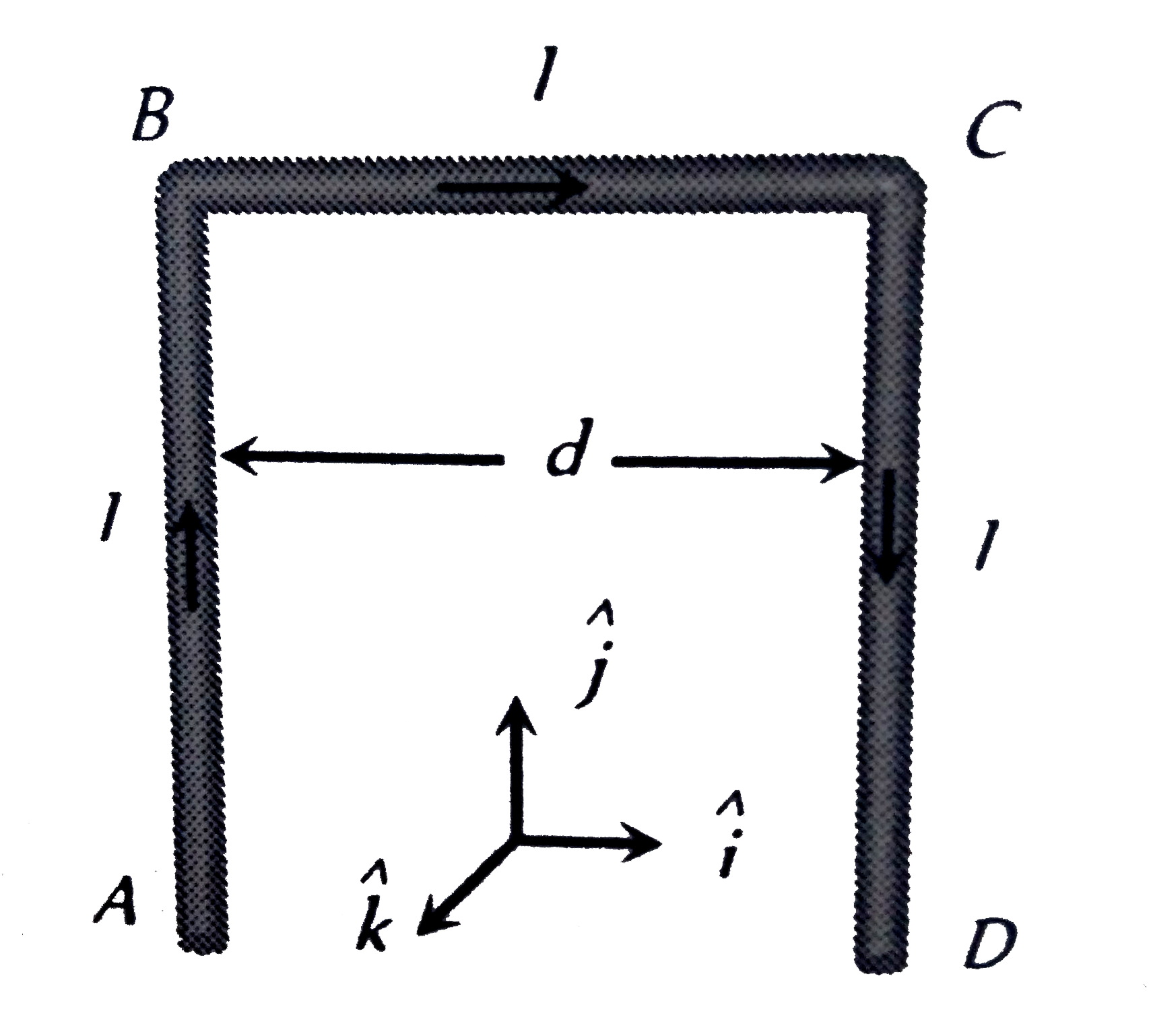 A−μ0I2πdˆkB−μ0IπdˆkC−μ0I4πdˆkD−μ0I8πdˆk
A−μ0I2πdˆkB−μ0IπdˆkC−μ0I4πdˆkD−μ0I8πdˆk
Three conductors carrying currents are perpcndicular to the plane of the drawing. They intersect the plane at three points that lie on a single straight line, wi th the distances from the middle conductor to the other two being equal. The currents in the outer conductors flow away from the reader, while the current in the middle conductor flows toward the reader. How is the magnetic Held vector directed at the point on the straight line that is perpendicular to the straight line passing through the three conductors in the plane of the drawing and is separated from the middle conductor by a distance equal to the distances between that conductor and the outer conductors? All three currents are equal in magnitude .
View SolutionIn a coaxial, straight cable, the central conductor and the outer conductor carry equal currents in opposite directions. The magnetic field is zero.
View SolutionTwo long parallel conductors carry currents i and 2I in the same direction. The magnetic induction at a point exactly mid way between them is B. If the current in the first conductor is reversed in direction, the magnetic induction at the same point will be
View SolutionA conductor AB of length L carrying a current I2, IS placed perpendicular to a long straight conductor XY carrying current I2, as shown in figure. The force on AB in magnitude is

View SolutionThe magnetic field at a perpendicular distance of 2 cm from an infinite straight current carrying conductor is 2×10−6 T. The current in the wire is
View Solution