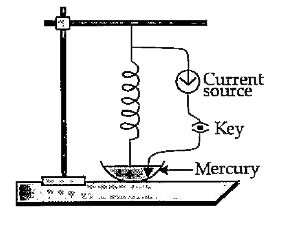
A loosely wound helix made of stiff metal wire is mounted vertically with the lower end just touching the mercury in a dish. When the current from a batter is started in the metal wire through the mercury, the wire executes oscillatory motion with the lower end jumping out of and into the mercury. Explain.
The windings of the metal helix carry currents in the same direction, therefore they experience attractive forces, pulling the lower end of metal wire out of mercury. When it happens, the circuit breaks, the current disappears and hence the force of attraction disappears. As a result of it, the wire helix regains its original position, completing the circuit again. The process is repeated time and again. Due to it, the oscillatory motion is set up.
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Conceptual Problems (d)
Explore 2 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Very Short Answer Questions (a)
Explore 2 Videos
- ELECTROSTATICSBook:PRADEEPChapter:ELECTROSTATICSExercise:ASSERTION-REASON TYPE QUESTIONS
Explore 2 Videos
- OPTICSBook:PRADEEPChapter:OPTICSExercise:Multiple choice questions
Explore 1 Video
Similar Questions
Attempt any 4 sub-parts out of 5. Each sub-part carries 1 mark.
Read the following text and answer the following questions on the basis of the same:
Roget's spiral:
Magnetic effects are generally smaller than electric effects. As a consequence, the force between currents is rather small, because of the smallness of the factor μ. Hence, it is difficult to demonstrate attraction or repulsion between currents. Thus, for 5 A current in each wire at a currents. Thus, for 5 A current in each wire at separation of 1 cm, the force per metre would be 5×10−4N, which is about 50 mg weight. It would be like pulling a wire by a string going over a pulley to which a 50 mg weight is attached. The displacement of the wire would be quite unnoticeable. With the use of a soft spring, we can increase the using mercury, we can make the displacement of even a few mm observable very dramatically. You will also need a constant-current supply giving a constant current of about 5 A. Take a soft spring whose natural period of oscillations is about 0.5-1s. Hang it vertically and attach a pointing tip to its lower end, as shown in the figure here. Take some mercury in a dish and adjust the spring such that the tip is just above the mercury surface. Take the DC current source, sonnect one of its terminals to the upper end of the spring and dip the other terminal in mercury. If the tip of the spring touches mercury, the circuit is completed through mercury. Let the DC source be put off to begin with. Let the tip be adjusted so that it just touches the mercury surface. Switch on the constant current supply and watch the fascinating outcome. The spring shrinks with a jerk, the tip comes out of mercury (just by a mm or so), the circuit is broken, the current stop, the spring relaxes and tries to comes back to its original position, the tip again touches mercury establishing a current in the circuit and the cycle continues with tick, tick, tick, ....
What else can be used instead of mercury in Roget's spiral?
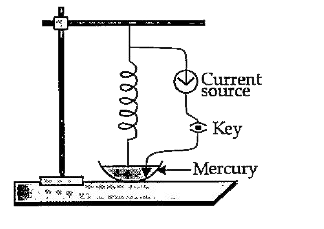
View SolutionAttempt any 4 sub-parts out of 5. Each sub-part carries 1 mark.
Read the following text and answer the following questions on the basis of the same:
Roget's spiral:
Magnetic effects are generally smaller than electric effects. As a consequence, the force between currents is rather small, because of the smallness of the factor μ. Hence, it is difficult to demonstrate attraction or repulsion between currents. Thus, for 5 A current in each wire at a currents. Thus, for 5 A current in each wire at separation of 1 cm, the force per metre would be 5×10−4N, which is about 50 mg weight. It would be like pulling a wire by a string going over a pulley to which a 50 mg weight is attached. The displacement of the wire would be quite unnoticeable. With the use of a soft spring, we can increase the using mercury, we can make the displacement of even a few mm observable very dramatically. You will also need a constant-current supply giving a constant current of about 5 A. Take a soft spring whose natural period of oscillations is about 0.5-1s. Hang it vertically and attach a pointing tip to its lower end, as shown in the figure here. Take some mercury in a dish and adjust the spring such that the tip is just above the mercury surface. Take the DC current source, sonnect one of its terminals to the upper end of the spring and dip the other terminal in mercury. If the tip of the spring touches mercury, the circuit is completed through mercury. Let the DC source be put off to begin with. Let the tip be adjusted so that it just touches the mercury surface. Switch on the constant current supply and watch the fascinating outcome. The spring shrinks with a jerk, the tip comes out of mercury (just by a mm or so), the circuit is broken, the current stop, the spring relaxes and tries to comes back to its original position, the tip again touches mercury establishing a current in the circuit and the cycle continues with tick, tick, tick, ....
Why the spring shrinks in Roget's spiral?
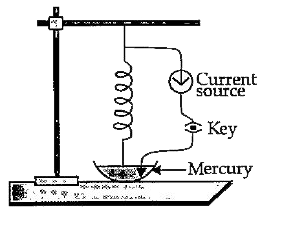
View Solution
Knowledge Check
A loosly wound helix made of stiff wire is mounted vertically with the lower end just touching a dish of mercury when a current from the battery is started in the coil through the mercury
Athe wire oscillatesBthe wire continues makes contactCthe wire breaks contact just when the current is passedDthe mercury will expand by heating due to passage of currentAssertion : A loosely round helix made of stiff wire is suspended vertically with the lower end just touching a dish of mercury. When a current is passed through the wire, the helical wire executes oscillatory motion with the lower end jumping out of and inside of mercury.
Reason : When electric current is passed through helix, a magnetic field is produced both inside and outside the helix.AIf both assertion and reason are true and the reason is the correct explanation of the assertion.BIf both assertion and reason are true but reason is not the correct explanation of the assertion.CIf assertion is true but reason is false.DIf the assertion and reason both are false.A metal wire of length L is suspended vertically from a rigid support. When a bob of mass M is attached to the lower end of wire, the elongation of the wire is l:
AThe loss in gravitational potential energy of mass M is Mgl.BThe elastic potential energy stored in the wire is MglCThe elastic potential energy stored in the wire is 12MglDHeat produced is loss of mechanical energy of system is 12Mgl
Attempt any 4 sub-parts out of 5. Each sub-part carries 1 mark.
Read the following text and answer the following questions on the basis of the same:
Roget's spiral:
Magnetic effects are generally smaller than electric effects. As a consequence, the force between currents is rather small, because of the smallness of the factor μ. Hence, it is difficult to demonstrate attraction or repulsion between currents. Thus, for 5 A current in each wire at a currents. Thus, for 5 A current in each wire at separation of 1 cm, the force per metre would be 5×10−4N, which is about 50 mg weight. It would be like pulling a wire by a string going over a pulley to which a 50 mg weight is attached. The displacement of the wire would be quite unnoticeable. With the use of a soft spring, we can increase the using mercury, we can make the displacement of even a few mm observable very dramatically. You will also need a constant-current supply giving a constant current of about 5 A. Take a soft spring whose natural period of oscillations is about 0.5-1s. Hang it vertically and attach a pointing tip to its lower end, as shown in the figure here. Take some mercury in a dish and adjust the spring such that the tip is just above the mercury surface. Take the DC current source, sonnect one of its terminals to the upper end of the spring and dip the other terminal in mercury. If the tip of the spring touches mercury, the circuit is completed through mercury. Let the DC source be put off to begin with. Let the tip be adjusted so that it just touches the mercury surface. Switch on the constant current supply and watch the fascinating outcome. The spring shrinks with a jerk, the tip comes out of mercury (just by a mm or so), the circuit is broken, the current stop, the spring relaxes and tries to comes back to its original position, the tip again touches mercury establishing a current in the circuit and the cycle continues with tick, tick, tick, ....
What are main 3 components in a Roget's spiral?
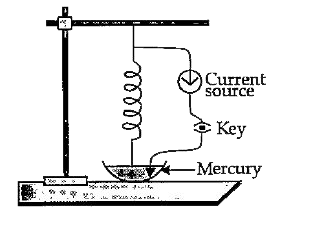
View SolutionAttempt any 4 sub-parts out of 5. Each sub-part carries 1 mark.
Read the following text and answer the following questions on the basis of the same:
Roget's spiral:
Magnetic effects are generally smaller than electric effects. As a consequence, the force between currents is rather small, because of the smallness of the factor μ. Hence, it is difficult to demonstrate attraction or repulsion between currents. Thus, for 5 A current in each wire at a currents. Thus, for 5 A current in each wire at separation of 1 cm, the force per metre would be 5×10−4N, which is about 50 mg weight. It would be like pulling a wire by a string going over a pulley to which a 50 mg weight is attached. The displacement of the wire would be quite unnoticeable. With the use of a soft spring, we can increase the using mercury, we can make the displacement of even a few mm observable very dramatically. You will also need a constant-current supply giving a constant current of about 5 A. Take a soft spring whose natural period of oscillations is about 0.5-1s. Hang it vertically and attach a pointing tip to its lower end, as shown in the figure here. Take some mercury in a dish and adjust the spring such that the tip is just above the mercury surface. Take the DC current source, sonnect one of its terminals to the upper end of the spring and dip the other terminal in mercury. If the tip of the spring touches mercury, the circuit is completed through mercury. Let the DC source be put off to begin with. Let the tip be adjusted so that it just touches the mercury surface. Switch on the constant current supply and watch the fascinating outcome. The spring shrinks with a jerk, the tip comes out of mercury (just by a mm or so), the circuit is broken, the current stop, the spring relaxes and tries to comes back to its original position, the tip again touches mercury establishing a current in the circuit and the cycle continues with tick, tick, tick, ....
Magnetic effects:
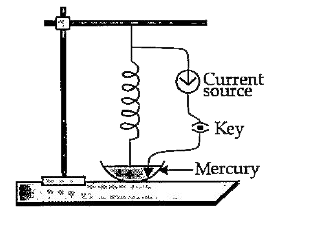
View SolutionAttempt any 4 sub-parts out of 5. Each sub-part carries 1 mark.
Read the following text and answer the following questions on the basis of the same:
Roget's spiral:
Magnetic effects are generally smaller than electric effects. As a consequence, the force between currents is rather small, because of the smallness of the factor μ. Hence, it is difficult to demonstrate attraction or repulsion between currents. Thus, for 5 A current in each wire at a currents. Thus, for 5 A current in each wire at separation of 1 cm, the force per metre would be 5×10−4N, which is about 50 mg weight. It would be like pulling a wire by a string going over a pulley to which a 50 mg weight is attached. The displacement of the wire would be quite unnoticeable. With the use of a soft spring, we can increase the using mercury, we can make the displacement of even a few mm observable very dramatically. You will also need a constant-current supply giving a constant current of about 5 A. Take a soft spring whose natural period of oscillations is about 0.5-1s. Hang it vertically and attach a pointing tip to its lower end, as shown in the figure here. Take some mercury in a dish and adjust the spring such that the tip is just above the mercury surface. Take the DC current source, sonnect one of its terminals to the upper end of the spring and dip the other terminal in mercury. If the tip of the spring touches mercury, the circuit is completed through mercury. Let the DC source be put off to begin with. Let the tip be adjusted so that it just touches the mercury surface. Switch on the constant current supply and watch the fascinating outcome. The spring shrinks with a jerk, the tip comes out of mercury (just by a mm or so), the circuit is broken, the current stop, the spring relaxes and tries to comes back to its original position, the tip again touches mercury establishing a current in the circuit and the cycle continues with tick, tick, tick, ....
The force 10−3 N, is equivalent to:
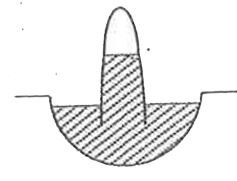
View SolutionTorricelli was the first do devise an experiment for measuring atmospheric pressure . He took calibrated hard glass tube , 1 m in lengt and of uniform cross section , closed at one end . He filled the whole tube with dry mercury taking care than no air or water droplets remain inside the tube , closed the opposite end of the tube tightly with thumb and inverted it . He put this inverted mercury tube into a mercury through , taking care that the end of the tube remains inside the mercury through , An interesting thing was noticed . Mercury in the tube fell down at first and then stopped at a particular position . The height was 76 cm above the free surface of mercury in the through . When the given tube was inclined or lowered in the mercury trough , the vertical haight of mercury level in the tube was always found constant .
Torricelli explained this by saying that the free surface of mercury in the trough . Hence , the hydrostatic pressure exerted by the trough measures the atmospheric pressure .
If this expriment uses water instead of mercury , then
View SolutionTorricelli was the first do devise an experiment for measuring atmospheric pressure . He took calibrated hard glass tube , 1 m in lengt and of uniform cross section , closed at one end . He filled the whole tube with dry mercury taking care than no air or water droplets remain inside the tube , closed the opposite end of the tube tightly with thumb and inverted it . He put this inverted mercury tube into a mercury through , taking care that the end of the tube remains inside the mercury through , An interesting thing was noticed . Mercury in the tube fell down at first and then stopped at a particular position . The height was 76 cm above the free surface of mercury in the through . When the given tube was inclined or lowered in the mercury trough , the vertical haight of mercury level in the tube was always found constant .
Torricelli explained this by saying that the free surface of mercury in the trough . Hence , the hydrostatic pressure exerted by the trough measures the atmospheric pressure .
If an additional hole is also made at P ' at the top point of the tube , then

View Solution

