If light passes near a massive object, the gravitational interaction causes a bending of the ray. This can be thought of as happening due to a change in the effective refractive index of the medium given by $n (r) = 1 + 2 G M / r c^{2}$
where $r$ is the distance of the point consideration from the centre of the mass of the massive body, $G$ is the universal gravitational constant, $M$ the mass of the body and $c$ the speed of light in vacuum. Considering a spherical object, find the deviation of the ray from the original path as it grazes the object.

Video Solution

Text Solution

Verified by Experts

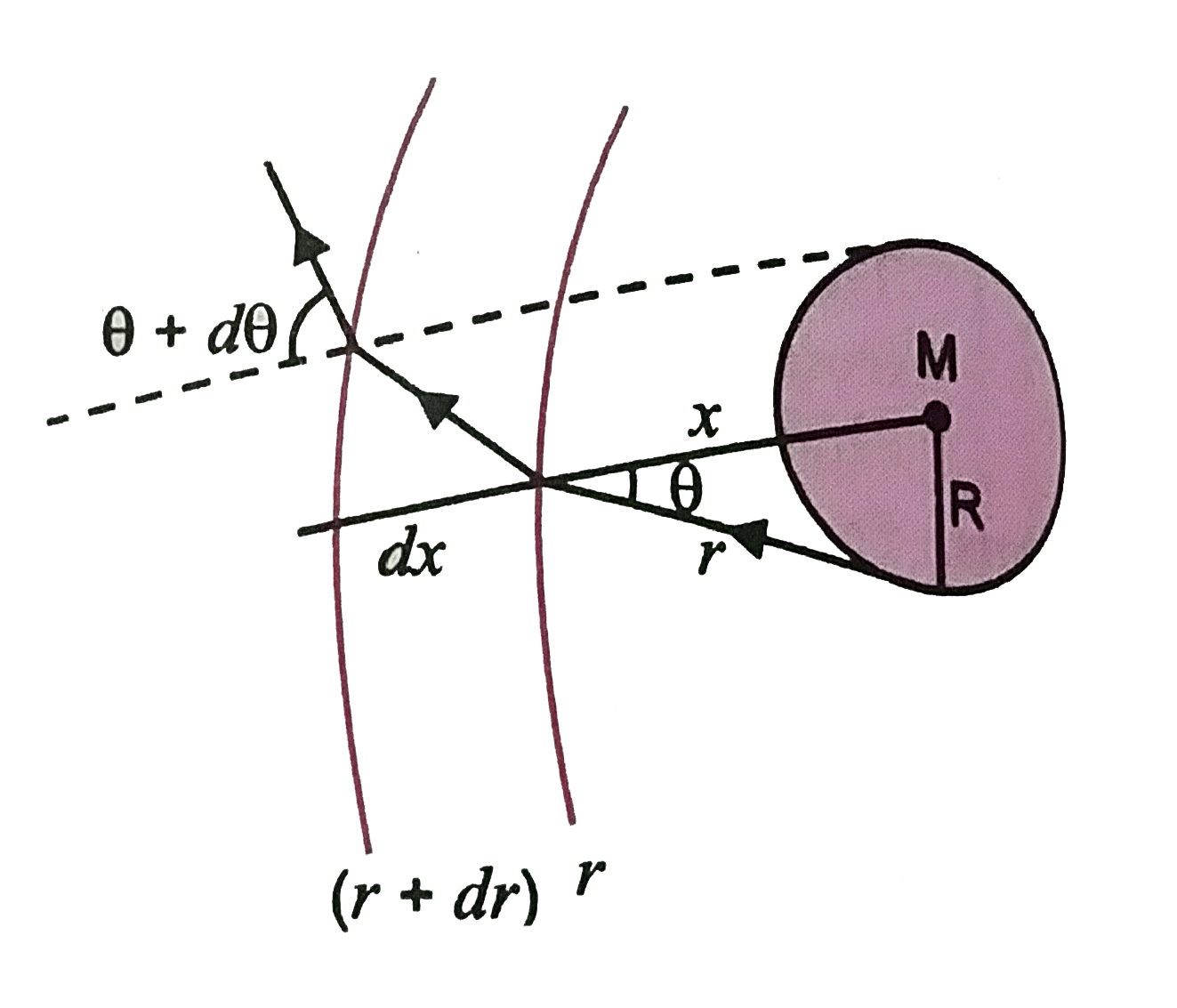
In Fig., we have shown a spherical massive body of mass $M$ and radius $R$ . Consider two planes one at $r$ and other at $(r + d r)$ from the centre of massive body. Let the light rays be incident at an angle $θ$ on the plane at $r$ and leave the plane at $(r + d r)$ at an angle $(θ + d θ)$ .
According to Snell's law,
$n (r) sin θ = n (r + d r) sin (θ + d θ) = [n (r) + \frac{d n}{d r} d r] (sin θ cos d θ + cos θ sin d θ)$
As $d θ$ is small, $cos d θ ≅ 1 and sin d θ ≅ d θ$
Neglecting products of differentials, we get
$n (r) sin θ = n (r) sin θ + n (r) cos θ d θ + \frac{d n}{d r} d r sin θ$ or $- \frac{d n}{d r} d r sin θ = n (r) cos θ d θ$
or $- \frac{d n}{d r} tan θ = n (r) \frac{d θ}{d r}$
As $n (r) = 1 + \frac{2 G M}{r c^{2}} ∴ \frac{d n}{d r} = \frac{- 2 G M}{r^{2} c^{2}}$
Put in (i) $\frac{2 G M}{r^{2} c^{2}} tan θ = (1 + \frac{2 G M}{r c^{2}}) \frac{d θ}{d r} ≅ \frac{d θ}{d r}$ $(∵ \frac{2 G M}{r c^{2}} < < 1)$
$d θ = \frac{2 G M}{c^{2}} \frac{tan θ}{r^{2}} d r$
Intergrating both sides, we get
$\int_{0}^{θ 0} d θ = \frac{2 G M}{c^{2}} \int_{- \infty}^{+ \infty} \frac{tan θ d r}{r^{2}} = \frac{2 G M}{c^{2}} \int_{- \infty}^{+ \infty} \frac{tan θ r d r}{r^{3}}$
Now, from (Fig. 11(EP).16), $r^{2} = x^{2} + R^{2}$ and $tan θ = \frac{R}{x}$
$∴ 2 r d r = 2 x d x ∴ \int_{0}^{θ 0} d θ = \frac{2 G M}{c^{2}} \int_{- \infty}^{+ \infty} \frac{R x d x}{x {(x^{2} + R^{2})}^{3 / 2}}$
If we put $x = R tan ϕ$ so that $d x = R {sec}^{2} ϕ d ϕ$ ,
then $\int_{0}^{θ 0} d θ = \frac{2 G M}{c^{2}} \int_{- π / 2}^{π / 2} \frac{R^{2} {sec}^{2} ϕ d ϕ}{R^{3} {sec}^{3} ϕ}$
$θ_{0} = \frac{2 G M}{R c^{2}} \int_{- π / 2}^{π / 2} cos ϕ d ϕ = \frac{4 G M}{R c^{2}}$
This is the deviation for the ray from the original path as it grazes the massive body.
.

Updated on:21/07/2023

The value of universal gravitational constant 'G' is
A $6.67 \times 10^{11} N m^{2} / K g^{2}$
B $6.67 \times 10^{- 11} N m^{2} / K g^{2}$
C $6.67 \times 10^{18} N m^{2} / K g^{2}$
D $6.67 \times 10^{- 18} N m^{2} / K g^{2}$
The escape velocity of a sphere of mass m is given by (G=Universal gravitational constant,M=Mass of the earth and $R_{e}$ =Radius of the earth)
A $\sqrt{\frac{2 G M m}{R_{e}}}$
B $\sqrt{\frac{2 G M}{R_{e}}}$
C $\sqrt{\frac{G M}{R_{e}}}$
D $\sqrt{\frac{2 G M m + R_{e}}{R_{e}}}$
The acceleration due to gravity'g' for objects on or near the surface of earth is related to the universal gravitational constant 'G' as ('M' is the mass of the earth and 'R' is its radius):
A $G = \frac{g (M)}{R^{2}}$
B $g = G \frac{M}{R^{2}}$
C $M = \frac{g G}{R^{2}}$
D $R = \frac{g G}{M^{2}}$