A ray of light incident on an equilateral triangular glass prism of μ=√3 moves parallel to the base of the prism inside it. What is the angle of incidence for this ray ?
When refracted ray is parallel to the base of the prism, deviation is minimum.
∴r=A/2=60/2=30∘
From μ=sinisinr
sini=μsinr=√3sin30∘=m√3/2
∴i=60∘.
Topper's Solved these Questions
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Solved Example(d)
Explore 32 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Conceptual problem(b)
Explore 22 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Solved Example(b)
Explore 61 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Multiple choice questions
Explore 7 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:Assertion- Reason Type questions
Explore 20 Videos
Similar Questions
A ray of light, incident on an equilateral glass prism (μg=√3) moves parallel to the base line of the prism inside it. Find the angle of incidence for this ray.
View SolutionA ray of light is incident on an equilateral triangular prism parallel to its base as shown in the figure. The ray just fails to emerge from the face AC. If μ be the refractive index of the prism then the relation(s) is/are :
View Solution
Knowledge Check
What is the angle of incidence for an equilateral prism of refractive index √3 so that the ray si parallel to the base inside the prism?
A30∘B45∘C60∘DEither 30∘ or 60∘When a monochromatic ray of light is passed through an equilatorial glass prism , it is found that the refracted ray in glass is parallel to the base of the prism . If i and e denote the angles of incidence and emergence respectively then
Ai>eBi<eCi=eDi+e=90∘A ray of light is incident on the hypotenuse of a right-angled prism after travelling parallel to the base inside the prism. If μ is the refractive index of the material of the prism, the maximum value of the base angle for which light is totally reflected from the hypotenuse is
Asin−1(Iμ)Btan−1(1μ)Csin−1(μ−1μ)Dcos−1(1μ)
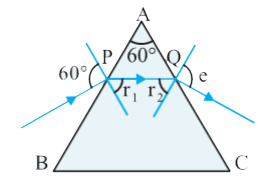
A ray of light is incident on one face of a prism (m=√3) at an angle of 60∘. The refracting angle of the prism is also 60∘. Find the angle of emergence .
View SolutionCalculate the speed of light in the prism if a ray of light is passing through an equilateral triangular glass prism from air and undergoes minimum deviation when angle of incidence is 5/4th of the angle of prism.
View SolutionA ray of light passing through an equilateral triangular glass prism from air undergoes minimum deviation when angle of incidence is 34th th of the angle of prism. Calculate the speed of light in the prism.
View SolutionA ray of light passing through an equilateral triangular glass prism from air undergoes minimum deviation when angle of incidence is 34th of the angle of prism. Calculate speed of light in prism.
View SolutionA ray of light passing through an equilateral triangular glass prism from air undergoes minimum deviation when angle of incidence is 3/4 th of the angle of prism. Calculate the speed of light in the prism.
View Solution

