Is the equation PV=RT valid for both, isothermal and adiabatic changes?
To determine whether the equation PV=RT is valid for both isothermal and adiabatic changes, we can analyze the definitions and conditions of these processes.
1. Understanding the Equation:
The equation PV=RT is known as the ideal gas law, where:
- P = pressure of the gas,
- V = volume of the gas,
- R = universal gas constant,
- T = absolute temperature of the gas.
2. Isothermal Process:
- An isothermal process occurs at a constant temperature.
- In this case, if the temperature T is constant, the product PV will also remain constant for a given amount of gas (assuming ideal behavior).
- Therefore, the equation PV=nRT (where n is the number of moles) holds true, as long as the temperature remains constant.
3. Adiabatic Process:
- An adiabatic process is characterized by no heat exchange with the surroundings.
- In an adiabatic process, the temperature of the gas can change due to work being done on or by the gas.
- However, the ideal gas law PV=nRT can still be applied at any given state of the gas, even though the relationship between P, V, and T will differ from that in an isothermal process.
4. Conclusion:
- The equation PV=RT is universally valid for any ideal gas, regardless of whether the process is isothermal or adiabatic.
- Thus, we conclude that PV=RT can be used in both isothermal and adiabatic processes.
Final Answer:
Yes, the equation PV=RT is valid for both isothermal and adiabatic changes.
The equation PV=RT is known as the ideal gas law, where:
- P = pressure of the gas,
- V = volume of the gas,
- R = universal gas constant,
- T = absolute temperature of the gas.
- An isothermal process occurs at a constant temperature.
- In this case, if the temperature T is constant, the product PV will also remain constant for a given amount of gas (assuming ideal behavior).
- Therefore, the equation PV=nRT (where n is the number of moles) holds true, as long as the temperature remains constant.
- An adiabatic process is characterized by no heat exchange with the surroundings.
- In an adiabatic process, the temperature of the gas can change due to work being done on or by the gas.
- However, the ideal gas law PV=nRT can still be applied at any given state of the gas, even though the relationship between P, V, and T will differ from that in an isothermal process.
- The equation PV=RT is universally valid for any ideal gas, regardless of whether the process is isothermal or adiabatic.
- Thus, we conclude that PV=RT can be used in both isothermal and adiabatic processes.
Yes, the equation PV=RT is valid for both isothermal and adiabatic changes.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Long answer questions
11 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Advanced problems for competitions
10 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Very short answer questions
31 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assertion- Reason Type questions
20 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assertion-Reason Type Questions
24 Videos
Similar Questions
Knowledge Check
The slope of isothermal and adiabatic curves are related as
Aisothermal curve slope = adiabatic curve slopeBisothermal curve slope = γ×adiabatic slopeCadiabatic curve slope = γ× isothermal slopeDadiabatic curve slope = (1/2) × isothermal curve slopeThe gas equatioon PV/2=RT, V stands for
Avolume of 2 grams of a gasBvolume of 2 moles of gasCvolume of 1 mole of gasDvolume of 1/2 mole of gas
Reversible Isothermal and Adiabatic process
View SolutionComparison of Isothermal and Adiabatic work
View SolutionAnalysis OF Isothermal and Adiabatic Process
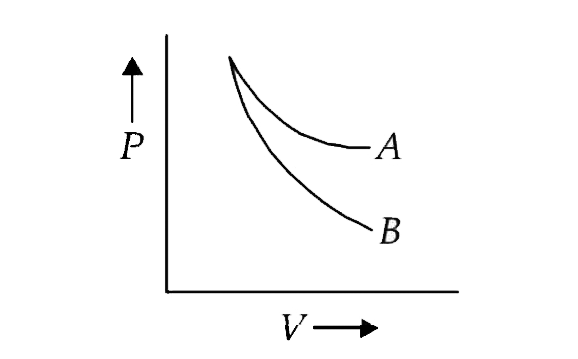
View SolutionThe curves A and B in the figure shown P-V graphs for an isothermal and an adiabatic process for an idea gas. The isothermal process is represented by the curve A.
View SolutionThe gas lawPVT= constant is true for
(A) Isothermal changes only
(B) Adiabatic changes only
(C)Both isothermal and adiabatic changes
(D) Neither isothermal nor adiabatic changes "
View SolutionIsothermal Process and Adiabatic Process.
View Solution
