A spring balance reads 10 kg when a bucket of water is suspended from it. What is the reading on the spring balance when (i) an ice cube of mass 1.5 kg is put into the bucket (ii) an iron piece of mass 7.8 kg suspended by another spring is immersed with half its volume inside the water n the bucket. Relative density of iron = 7.8
The correct Answer is:(i) 11.5 kg f (ii) 10.5 kg f
To solve the problem step by step, we will analyze both parts of the question regarding the spring balance readings.
Part (i): Ice Cube in the Bucket
1. Initial Reading of the Spring Balance: The spring balance reads 10 kg when the bucket of water is suspended from it. This means the weight of the bucket and water combined is 10 kg.
2. Adding the Ice Cube: When we add an ice cube with a mass of 1.5 kg to the bucket, we need to consider the total weight that the spring balance will now measure.
3. Calculating the New Reading:
- The new weight = Initial weight + Weight of the ice cube
- New weight = 10 kg + 1.5 kg = 11.5 kg
4. Final Reading: Therefore, the reading on the spring balance after adding the ice cube will be 11.5 kg.
Part (ii): Iron Piece Immersed in Water
1. Understanding the Iron Piece: We have an iron piece with a mass of 7.8 kg and a relative density of 7.8. This means the density of iron is 7.8 times that of water.
2. Calculating the Volume of the Iron Piece:
- Density of iron = 7.8 x 10³ kg/m³ (since the density of water is 1 x 10³ kg/m³).
- Volume of the iron piece = Mass / Density = 7.8 kg / (7.8 x 10³ kg/m³) = 1 x 10^-3 m³.
3. Determining the Volume Immersed: Since half of the iron piece is immersed in water, the volume submerged (V') is:
- V' = (1 x 10^-3 m³) / 2 = 0.5 x 10^-3 m³.
4. Calculating the Upward Thrust (Buoyant Force):
- Buoyant force (thrust) = Volume submerged x Density of water x g
- Buoyant force = (0.5 x 10^-3 m³) x (1 x 10³ kg/m³) x (9.8 m/s²) = 4.9 N.
5. Converting Buoyant Force to kgf:
- 1 kgf = 9.8 N, so the buoyant force in kgf = 4.9 N / 9.8 N/kgf = 0.5 kgf.
6. Calculating the Total Reading on the Spring Balance:
- Initial reading (bucket + water) = 10 kg.
- The upward thrust (buoyant force) = 0.5 kgf.
- Total reading = Initial weight + Buoyant force = 10 kg + 0.5 kg = 10.5 kg.
7. Final Reading: Therefore, the reading on the spring balance when the iron piece is immersed will be 10.5 kg.
Summary of Answers:
- (i) The reading on the spring balance after adding the ice cube is 11.5 kg.
- (ii) The reading on the spring balance after immersing the iron piece is 10.5 kg.
- The new weight = Initial weight + Weight of the ice cube
- New weight = 10 kg + 1.5 kg = 11.5 kg
- Density of iron = 7.8 x 10³ kg/m³ (since the density of water is 1 x 10³ kg/m³).
- Volume of the iron piece = Mass / Density = 7.8 kg / (7.8 x 10³ kg/m³) = 1 x 10^-3 m³.
- V' = (1 x 10^-3 m³) / 2 = 0.5 x 10^-3 m³.
- Buoyant force (thrust) = Volume submerged x Density of water x g
- Buoyant force = (0.5 x 10^-3 m³) x (1 x 10³ kg/m³) x (9.8 m/s²) = 4.9 N.
- 1 kgf = 9.8 N, so the buoyant force in kgf = 4.9 N / 9.8 N/kgf = 0.5 kgf.
- Initial reading (bucket + water) = 10 kg.
- The upward thrust (buoyant force) = 0.5 kgf.
- Total reading = Initial weight + Buoyant force = 10 kg + 0.5 kg = 10.5 kg.
- (i) The reading on the spring balance after adding the ice cube is 11.5 kg.
- (ii) The reading on the spring balance after immersing the iron piece is 10.5 kg.
Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Multiple choice questions-II
Explore 14 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Multiple choice questions-I
Explore 173 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Fill in the Blanks E
Explore 10 Videos
- PHYSICAL WORLD AND MEASUREMENTBook:PRADEEPChapter:PHYSICAL WORLD AND MEASUREMENTExercise:Competiton Focus Jee Medical Entrance
Explore 18 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(a)
Explore 25 Videos
Similar Questions
A bucket of water is suspended from a spring balance. What happens to reading of balance
(a) when a piece of stone suspended from a string is immersed in the water without touching the bucket
(b) when a piece of lead or cork is put in the water in the bucket.
View SolutionThe reading of a spring balance when a block is suspended from it iin air is 60 N the reading is changed to 40 N when the block is submerged in water. Find the relative density of the block.
View Solution
Knowledge Check
A spring balance reads 10kg when a bucket of water is suspened from it . What will be the reading of the balance when an iron piece of mass 7.2kg suspended by a string is immersed with half its volume inside the water in the bucket? Relative density of iron is 7.2
A10kgB10.5kgC13.6kgD17.2kgAs shown in the figure, two equal masses each of 2kg are suspended from a spring balance. The reading of the spring balance will be.
 AZeroB2kgC4kgDBetween zero and 2kg
AZeroB2kgC4kgDBetween zero and 2kgA spring balance shows 100 gf reading when a metallic sphere is suspended from its hook. When the completely immersed in water, the reading shown by the balance is 75gf. The relative density of the material of the sphere is
A1B2C3D4
A man standing in a lift holds a spring balance with a load of 5kg suspended from it What would be the reading of the balance when the lift is descending with an acceleration of 3.8m/s2 .
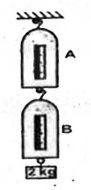
View SolutionA block of mass 2kg is suspended through two light spring balances A and B. Then A and B will read respectively
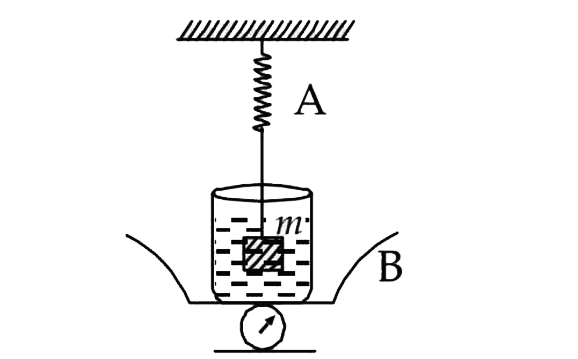
View SolutionThe spring balance A reads 2 kg with a block m suspended from it. A balance B reads 5kg when a beaker with liquid is put on the pan of the balance. The two balances are now so arranged that the hanging mass in inside the liquid in the beaker as shown in the figure. In this situation:
View SolutionThe reading of a spring balance when a mass is weighed on it in air is 40 gm. When the mass is immersed in water, its reading is 20 gm. The specific gravity of the mass is
View SolutionThe reading of a spring balance when a block is suspended from it in air is 60 N. This reading is changed to 40 N when the block is submerged in water. The relative density of the block is:
View Solution

