An equilateral triangle ABC if formed by two Cu rods AB and BC and one Al rod

it is heated in such a way that temperature of each rod increases by $Δ T .$ Find change in the angle ABC. [Coeff. Of linear expansion for Cu. is $α_{1},$ Coeff. of linear expansion for Al is $α_{2}]$

Video Solution

Text Solution

Verified by Experts

Refer

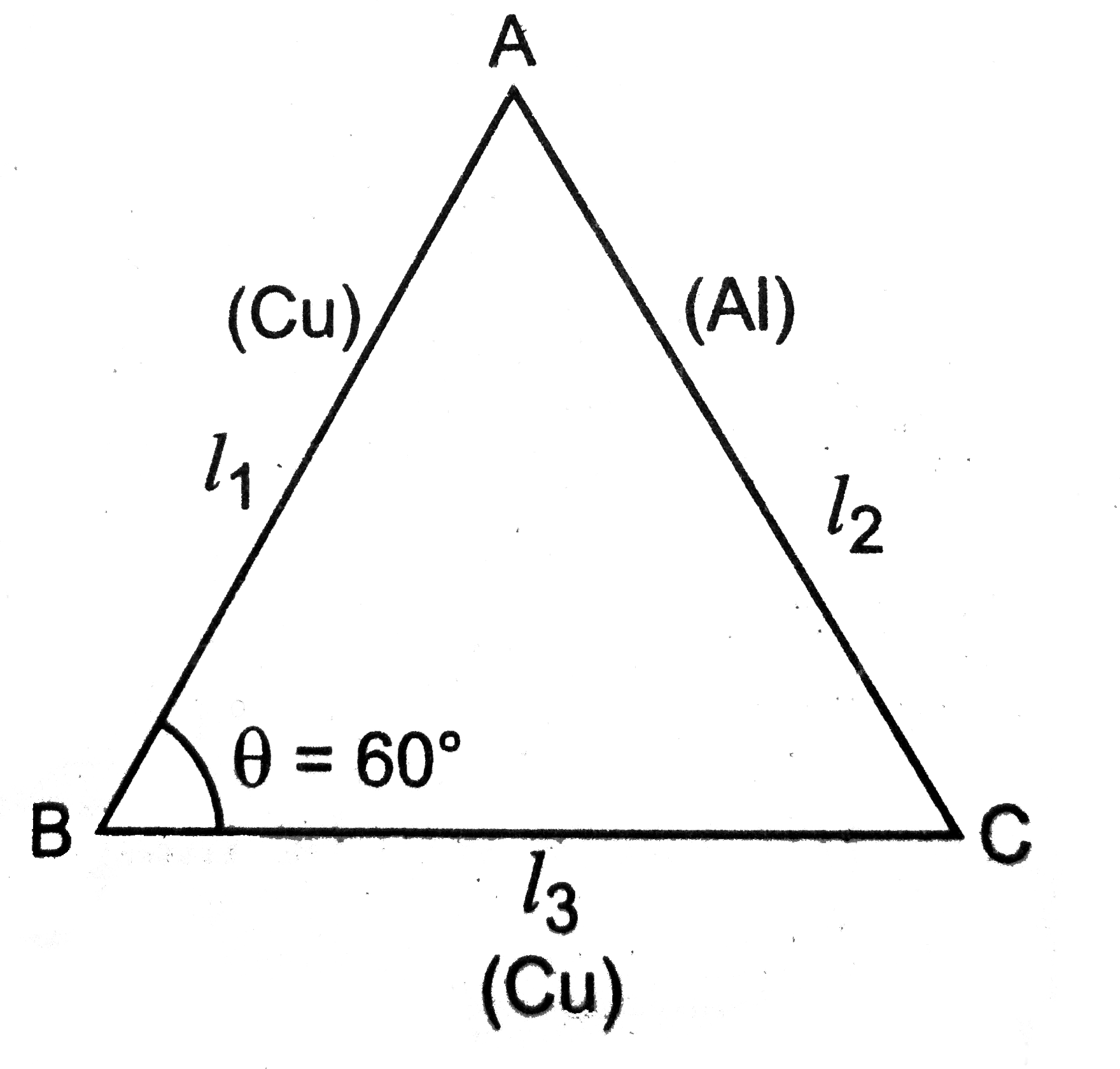
$cos θ = \frac{l_{1}^{2} + L_{3}^{2} - l_{2}^{2}}{2 l_{1} l_{3}}$
$2 l_{1} cos θ = l_{1}^{2} + l_{3}^{2} - l_{2}^{2}$
Differentiating it we have $2 (l_{1} d l_{3} + l_{3} d l_{1}) cos θ - 2 l_{1} l_{3} sin θ d θ = 2 l_{1} d l_{1} + 2 l_{3} d l_{3} - 2 l_{2} d l_{2}$
Here, $l_{1} = l_{2} = l_{3} l, d l_{1} = l α_{1} Δ T, d l_{2} = l α_{2} Δ T and d l_{3} = l α_{1} Δ T$
$∴ 2 (l \times l α_{1} Δ T + l \times l α_{1} Δ T) cos θ - 2 l \times l sin θ d θ$
$= 2 l \times l α_{1} Δ T + 2 l \times l α_{1} Δ T - 2 l \times l α_{2} Δ T$
Dividing it by $2 l^{2}$ we get $2 α_{1} Δ T cos θ - sin θ d θ = 2 α_{1} Δ T - (α_{2} Δ T)$
$sin θ d θ = 2 α_{1} Δ T (cos θ - 1) + α_{2} Δ T$
Using $θ = 60^{\circ}$ we have $\frac{\sqrt{3}}{2} d θ = 2 α_{1} Δ T (\frac{1}{2} - 1) + α_{2} Δ T = (α_{2} - α_{1}) Δ T ∴ d θ = (α_{2} - α_{1}) Δ T \times \frac{2}{\sqrt{3}}$

Updated on:21/07/2023