Two liquids of densities $r h p_{1} and ρ_{2}$ coefficient of viscosity $η_{1} and η_{2}$ are found to flow through a capillary tube at the same rate. What is the ration of $η_{1} / η_{2}$ ?

Video Solution

Text Solution

Verified by Experts

As rate of flow of liquid
$V = \frac{η_{1}}{ρ_{1}} = \frac{η_{2}}{ρ_{2}} or \frac{η_{1}}{η_{2}} = \frac{ρ_{1}}{ρ_{2}}$ .

Updated on:21/07/2023

The coefficient of viscosity $η$ of a liquid can be defined from the equation
A $F = η u \frac{d A}{d x}$
B $F = η A \frac{d u}{d x}$
C $F = η A \frac{d x}{d u}$
D $F = η u \frac{d x}{d A}$
A liquid of density $ρ$ and coefficient of viscosity $η$ , flows with velocity $υ$ through a tube of diameter D. A quantity $R = \frac{ρ υ D}{η}$ determines whether the flow will be streamlined or turbulent. R has the dimension of
Avelocity
Bacceleration
Cforce
Dnone of these
A thin horizontal movable plate P is separated from two fixed horizontal plates $P_{1}$ and $P_{2}$ by two highly viscous liquids of coefficient of viscosity $η_{1}$ and $η_{2}$ as shown, where $η_{2} = 4 η_{1}$ . Area of contact of movable plate with each fluid is same. If the distance between two fixed plates is h, then the distance h1 of movable plate from upper fixed plate such that the movable plate can be moved with a constant velocity by applying a minimum constant horizontal force F on movable plate is (assume velocity gradient to be uniform in each liquid).

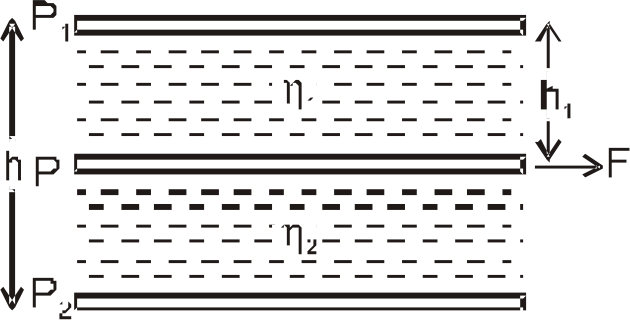Ah/4
Bh/2
C2h/3
Dh/3